基于ansys workbench的蜗杆斜齿轮静力学仿真

赵 葵，刘海岷，雷海胜，郁向红

(1.武汉工业学院机械工程学院湖北武汉430023;2.安徽理工大学机械工程学院安徽淮南232001)

蜗杆斜齿轮传动是在传统的蜗杆蜗轮传动中用斜齿轮取代蜗轮形成的传动副，由于蜗轮齿廓形状复杂，齿面无法磨削，因此加工精度较低，一般不进行齿面热处理，齿面硬度小。渐开线圆柱斜齿轮的加工相对较易、加工效率高，且可以对齿面进行淬硬后的磨削加工，齿面精度和硬度较高;所以它既保持了蜗杆蜗轮副传动的优点，又克服了蜗轮加工困难的缺点，从而形成了一种新的传动方式，因此目前很多机构上都采用了这种新型传动方式。因此，研究该传动副在工作状态下的静力学特性，正确计算啮合过程中的应力应变就格外重要。本文以UG软件为平台进行蜗杆斜齿轮副的三维建模，利用有限元分析软件ansys workbench进行静力学分析，为设计者提供了一种正确计算啮合过程中应力应变的方法。

1 蜗杆斜齿轮模型的建立

渐开线蜗杆可视为一个齿数等于蜗杆头数的大螺旋角(β=90-γ)斜齿圆柱齿轮［1］。根据齿轮手册可以得到蜗杆是一个斜齿轮，并且是一个大螺旋角的斜齿轮。因此，蜗杆副中蜗杆与斜齿轮的啮合就可以看做是两个斜齿轮的啮合，即交错轴斜齿轮传动。由此可得蜗杆和斜齿轮啮合条件如下：(1)蜗杆与斜齿轮的法面模数与法面压力角相等;(2)蜗杆导程角等于斜齿轮的螺旋角;(3)蜗杆旋向与斜齿轮旋向相同。只要同时满足这三个条件，蜗杆和斜齿轮就能实现啮合，并且在工作过程中稳定性好。

进行有限元分析前必须建立蜗杆斜齿轮啮合的模型，有限元分析数据是否精确取决于模型的正确性，本文选用的是渐开线蜗杆和渐开线斜齿轮，因此在渐开线形成的基础上建立蜗杆斜齿轮的模型可以保证模型的正确性。两模型的旋转方向都为右旋，采用三维制图软件UG进行精确建模和装配。渐开线蜗杆的精确建模方法有很多，这里采用的是先画出端面齿廓，已知这种断面齿廓为渐开线，如果将此端面齿廓沿蜗杆的螺旋线扫描，就能够得到蜗杆的轮齿模型［2］。蜗杆断面齿廓方程如下：

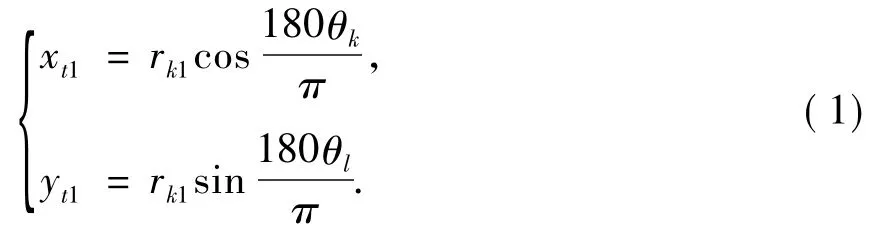
斜齿轮渐开线曲线方程：

其中：

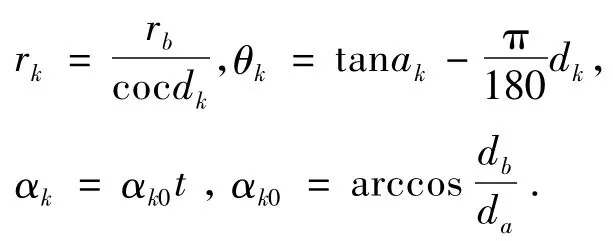
式中：rb——基圆半径;

rk——渐开线上任意一点的矢径;

rk1——蜗杆渐开线上任意一点的矢径;

rk2——斜齿轮渐开线上任意一点的矢径;

θk——AK 段得展角;

αk——渐开线在k点的压力角;

db——斜齿轮齿顶圆直径;

da——蜗杆齿顶圆直径;

αk0——渐开线终止角。

在建模时需要将方程式转化成三维建模软件可以识别的表达式，利用UG的曲线方程功能可以建立蜗杆和斜齿轮的渐开线模型。表达式如下。

蜗杆断面齿廓渐开线表达式：

alpha(k0)=deg(arcos(db/da);

alpha(k)=alpha(ko)*t;

rk=rb/cos(alpha(k));

theta(k)=deg(tan(alpha(k))-deg(alpha(k));

t=1，(建模软件内部系统变量，变量范围为0～1)

xt1=rk*cos(deg(theta(ak)));

yt1=rk*sin(deg(theta(ak)));

zt1=0。

斜齿轮渐开线表达式：

xt2=rk2*sin(deg(alpha(k)))-rk2*alpha(k)*cos(alpha(k);

yt2=rk2*sin(deg(alpha(k)))+rk2* alpha(k)*cos(deg(alpha(k)));

zt2=0。

与蜗轮传动相比较，蜗杆斜齿轮传动具有以下优点。

(1)斜齿轮容易加工、制造成本低、效率高。

(2)蜗轮齿面因无法磨削而不能达到很高的精度，而斜齿轮可以磨削，从而能加工出高精度的斜齿轮，并可以用于硬齿面，提高承载能力。

(3)蜗杆斜齿轮传动啮合时，齿面理论上是点接触，受载后成局部区域接触，因此，它属于失配蜗杆传动副，具有良好的润滑性，从而提高承载能力。

因此蜗杆斜齿轮可以成为一种易加工、高精度、高承载能力的传动形式。目前这种传动副运用日益广泛，如车床C616的溜板箱，数控转台等。为了解决此传动方式在有限元理论分析方面的不足，本文采用ansys workbench有限元分析软件对啮合进行静力学分析。

2 蜗杆斜齿轮啮合ansys workbench有限元分析

2.1 文件导入

建立三维模型后以 x_t格式导入 ansys workbench中，得到在ansys中的蜗杆斜齿轮装配的几何模型，如图1所示。

图1 蜗杆斜齿轮啮合

2.2 设置材料属性

在engineering data菜单中选择general materials下的structural steel并添加，在engineering data中修改材料名、弹性模量、泊松比、材料密度。蜗杆采用的材料选用20 Cr，其物理参数为：弹性模量E1=206 GPa，泊松比 ν1=0.3 ，质量密度为 ρ1=7.82 ×103kg/m3;斜齿轮选用40 Cr，其物理参数为：弹性模量E2=206 GPa泊松比ν2=0.28，质量密度为ρ2=7.82 × 103kg/m3。

2.3 划分网格

在geometry菜单下选择replace geometry，浏览已经被转化成 x_t格式的模型，并选择蜗杆assignment为 20 Cr，斜齿轮 assignment为 40 Cr。

由于计算机硬件条件的限制，本文网格划分方式先采用自由划分网格，在mesh菜单下将element size设置为50 mm，然后对啮合的齿面用refinement和size功能进行细化。啮合过程中受力最明显的点在啮合齿面上。所以对啮合齿面细化网格可以在现有的计算机硬件的条件下提高啮合齿面变形量计算结果的精确度。网格模型如图2所示。

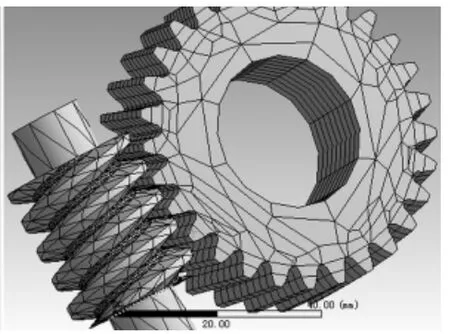
图2 网格线划分

2.4 边界条件

为了保证蜗杆斜齿轮正常工作，必须约束蜗杆和斜齿轮的轴向、径向移动和X、Y、Z这5个方向的自由度，保证它们只有一个绕轴线旋转的运动。因此对蜗杆斜齿轮啮合添加的是Frictionless support(无摩擦约束)，在Connections中对蜗杆和斜齿轮各添加一个 Revolute-ground约束 ，并在 Static structural中给蜗杆和斜齿轮添加Cylindrical support(圆柱面约束)［3］，在斜齿轮上添加一个旋转力矩Moment，斜齿轮旋转驱动蜗杆。蜗杆在阻力的作用下达到平衡，并对斜齿轮产生一个反力矩，两齿轮通过轮齿接触传递转矩，虽然工作状态下蜗杆和斜齿轮变形量都很小，但是为了提高数据真实性和准确性［4］，本文选用的材料都是柔性体，与实际工作情况相符。

2.5 求解计算

通过ansys workbench软件计算出接触齿在法向的应力与应变，在ansys workbench的solution菜单中加入各种probe可以得到需要的结果，例如应力、应变量、各个轴向位移等。应力、应变结果如图3、图4所示。在ansys workbench求解结果中颜色越深表示应力和应变量越大。从图中可以看出由于在接触点附近，齿轮和蜗杆受到的扭矩和反力矩较大，所以在接触点附近的应力与应变最为明显，而这个最大的点是斜齿轮和蜗杆的啮合点。通过ansys workbench求解能得到此点受到的最大应力和最大应变量如表1所示。

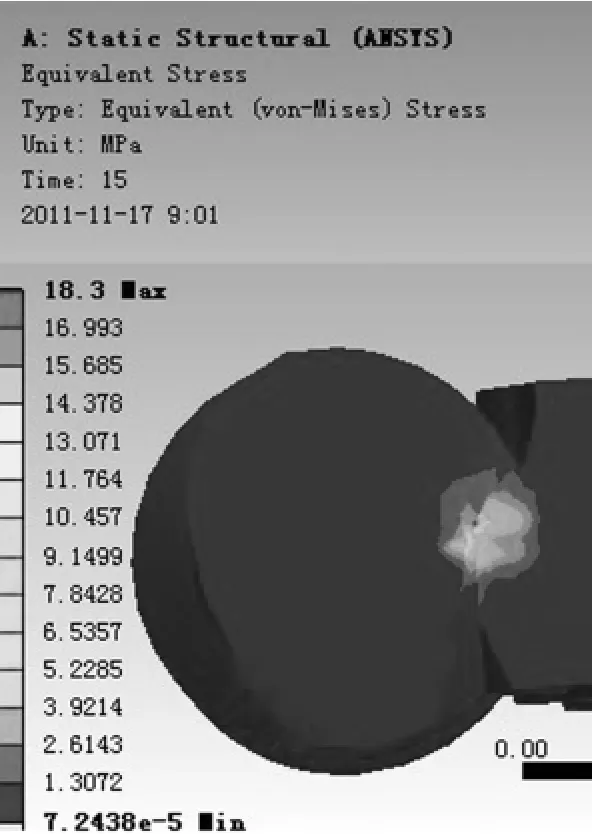
图3 蜗杆斜齿轮应力云图

图4 蜗杆斜齿轮啮合应变云图

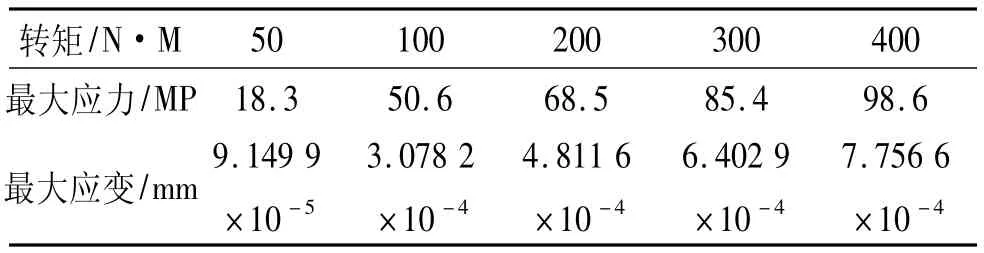
表1 不同转矩下啮合点的最大应力与应变量

3 结论

本文阐述了蜗杆斜齿轮啮合从实体建模到有限元分析求解静力学特性的完整过程，利用最新版本的ansys12.0分析软件中的ansys workbench分析蜗杆斜齿轮啮合情况，详细地介绍建模以及仿真步骤，得到啮合区域每个点的最大应力与应变量，本文所提出的分析方法适用于各种型号的蜗杆和斜齿轮啮合情况，为这种新型传动方式的仿真分析打下了坚实的基础。通过计算出的应力和应变量，设计者可以迅速、准确地进行设计方案的绘图、分析和确定技术工作，缩短设计周期，提高设计质量，为蜗杆斜齿轮设计时的力学特性计算提供了方法和参考依据。

［1］ 叶克明.齿轮手册.［M］北京：机械工业出版社，1990.

［2］ 杨玲玲，胡树根，林小哲，渐开线蜗杆在UG中的精确建模［J］.轻工机械，2007，25(3)：74-76.

［3］ 刘晓军，施永强，王伟.基于 ansys workbench的复合齿轮泵啮合齿轮有限元分析［J］.煤矿机械2009，30(5)：52-54.

［4］ 童林军，李晓珍，彭志刚.基于 ansys/ls-dyna的齿轮传动动力学特性分析［J］.拖拉机与农用运输车，2010，37(2)：33-34.