中医方剂内在规律的数学方法研究进展

张 砚，王益民，刘 霞

中医方剂内在规律的数学方法研究进展

张 砚，王益民，刘 霞

中医方剂；内在规律；数学方法；线性；函数

中医方剂是个系统的知识体系，其配伍规律是中医药理论的灵魂。中医现代化发展的一个重点，即是借助数学方法来研究中医方剂配伍规律，以推动中医的现代化进程。近年来对中医方剂内在规律的数学方法研究主要有以下几方面。

1 线性分析方法

盛志刚等[1]从传统中医方剂理论出发，借鉴现代工程科学的一些计算方法，从一个新的角度——方剂定量计算来审视方剂的作用。将中药的性味归经、气血阴阳等都各自以百分比例形式近似定量，并以“八珍汤”和“凉开三宝”为例进行了分析，通过对各中药性味归经等的定量化，使中药的作用效果能够更加的直观化，实现了将模糊的中医理论描述转化为可见的具体定量，使中药具有了统一的可对比性。

颜素容等[2]以传统配伍理论为基础，将中医方剂药性指标进行了量化。选取了24个药性作为基本指标，药性赋值的表现形式采用二值逻辑变量赋值。并将方剂中的n味药按药性取值构成一个n×m维药性矩阵F；以方剂中各味药的用药量占本方剂总用药量的比重形成用量百分比矩阵X；得到方剂药性特征矩阵Y=XF（如公式1所示）。通过方剂药性特征矩阵可直观地探究中医方剂的配伍特性，为研究药性与方剂间的规律奠定了基础，为研究各类方剂特性的异同提供了依据，为中医方剂的优化、开发等提供了方法。公式（1）为：

王文刚[3]针对不同版本《方剂学》教材中对方剂的君臣佐使药认定不同的现象，提出量效分析法。按药典中规定的中药用量Xmin~Xmax，取其中位数Z=（Xmin+Xmax）/2，中药在该方剂中的相对值F=A（实际用量）/Z，通过此方法计算出复方大承气汤、大承气汤、小承气汤、调胃承气汤4个方子各自的F值之和为 14.82、7.40、3.28、2.98，由此得出这 4 个方子的泻下功效是逐渐减低的。此方法在应用中存在实际称量中的误差等问题，但一定程度上能对方中药物的重要性作出明确分析，有利于提取方中主要药物，能够对药物繁多的巨大方剂进行分析、筛选、精简。

2 函数分析法

任廷革等[4]针对中医方剂诸因子间存在的“量效关系”、“药效关系”、“证效关系”、“候效关系”等，建立了方剂功效量化的数学模型。为将复杂的方剂药物和用量转化为易于操作的有效数据，提出了“相对药量”的概念及计算方法，得到了药物剂量在其历史用药范围中的权重，使得各药物在方剂中的贡献度有了一定的可比性。

相对药量计算如公式（2）所示：

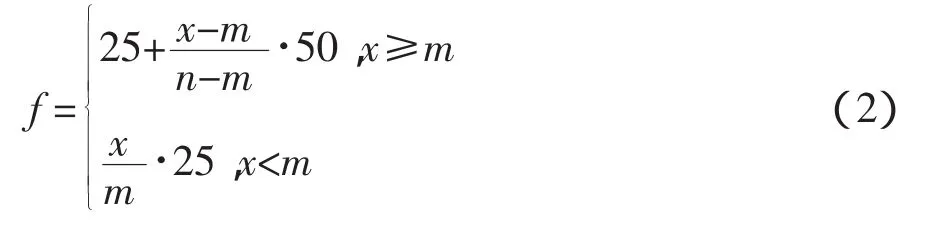
式中：m—最小药量（常用药量的下限）；n—最大药量（常用药量的上限）；x—实际药量；f—相对药量（无纲量）。

高全泉等[5]指出“相对药量”表现的是用药力度大小，将用药质量转化成了该药物的药效对方剂功效预期作用的强弱，因此提出将“相对药量”之称改为更为贴切的“药量强度”。并将相对药量的计算公式如下所示，进行了改进和细化，得到了“药量强度”的计算公式，其函数分别为二次函数、分段函数和直线函数，较好的展现了中医方剂的整体性和多元性。

药量强度计算如公式（3）所示：≤

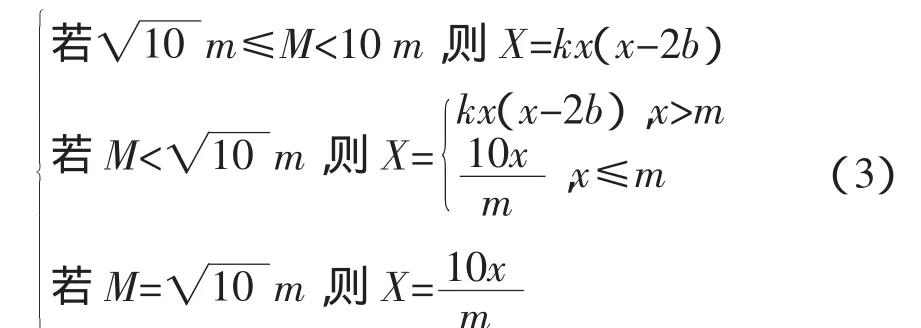
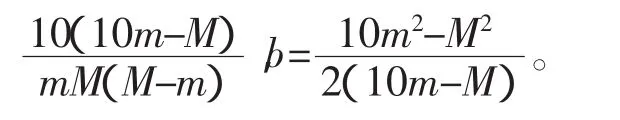
顾作林等[7]对比分析了几种“相对药量”模型体系，运用微分方程理论，指出药效是中药剂量的单调递增函数，但增长速度却是多种形式的，并提出了直线模型、指数函数模型、对数函数模型、二次函数模型等5种表现形式：进一步体现了中药本身的复杂性能，同时也肯定了归一化的处理思想。

直线模型如公式（4）所示：

3 集合分析方法

李江龙等[8]提出运用粗糙集理论在治疗某种疾病的原有处方的基础之上，设计出若干个新配方，通过对此决策表进行一系列知识约简，最终得到符合要求的属性集合。依据其所给出的实例，在条件属性C{C|C=a，…，i}之下，9个新配方的临床试验的9组对象U，形成了3大类决策属性U/C={{1，2，3，5，9}，{4，8},{6，7}}，即决策表中决策属性 D{D=L，H，B}，代表了3种临床效果：L——与原处方效果相同，H——效果有提升，B——效果下降。经过一系列的约简可得到新处方的基本成分，再借助其他多种分析手段进行方剂辅助用药的选择，能够优化筛选，有效缩短对中医方剂的研发周期，为研究中药配伍规律提供了新的技术途径和分析方法。见表1。

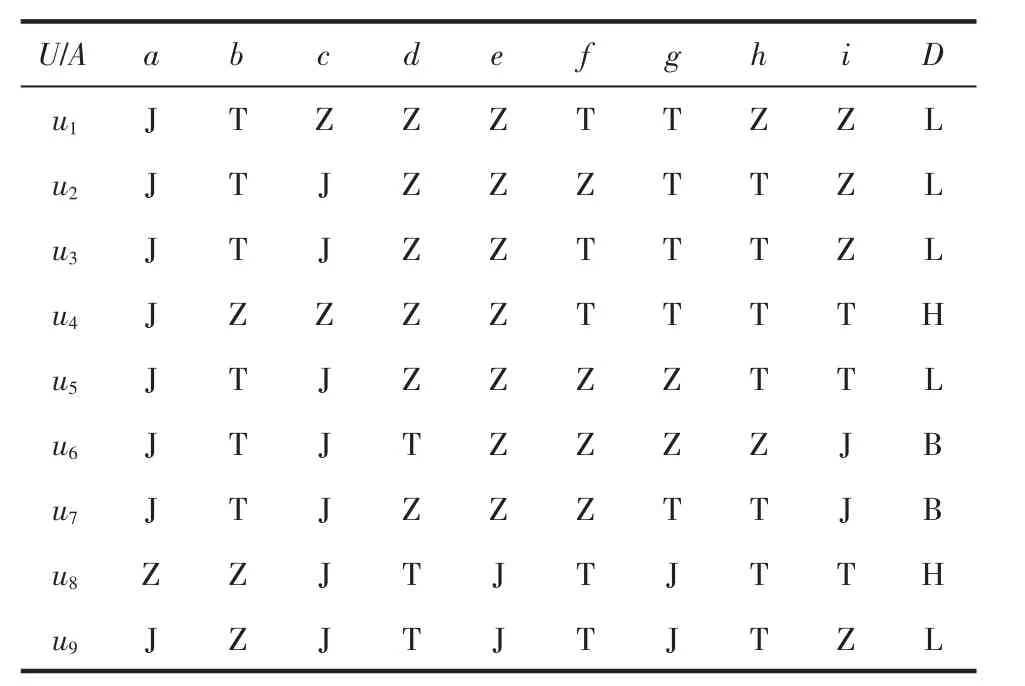
表1 处方优化决策表

于润桥等[7]将中医方剂作为中医方证系统来研究，运用粗糙集理论来阐释中医方证体系的不确定性和复杂性等。结合多元分析中主成分分析的方法对论域进行分类，对影响因素的权系数进行计算后提取出确定性的和不确定性的相关关系规则，对中药君臣佐使关系的分析及中药方剂的优化、改进具有指导作用。见图1。

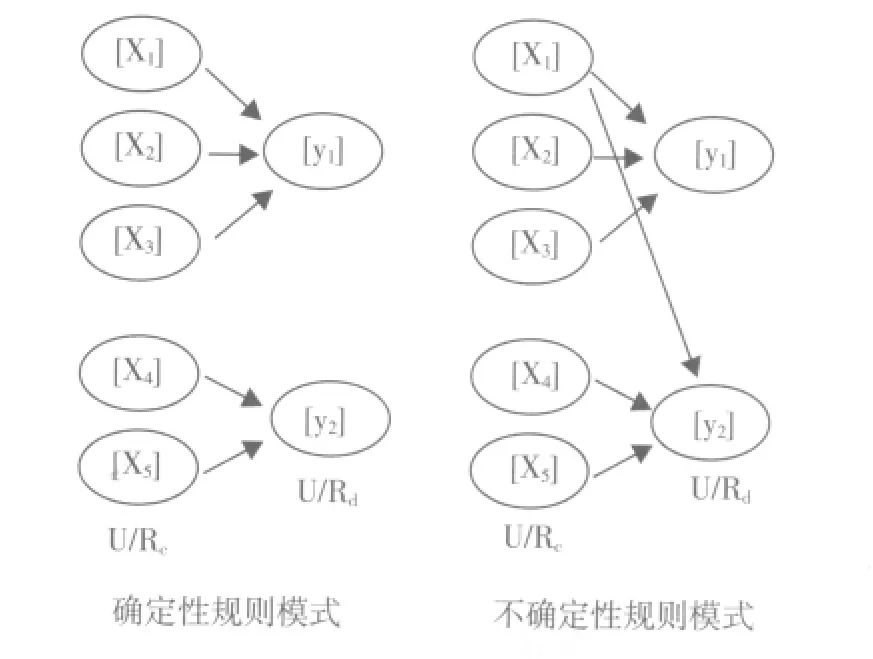
图1 相关关系规则示意图

危荃等[9］复制肾阳虚大鼠模型，采用右归丸不同配比药液干预，并应用粗糙集理论建立起药物与证候指标之间的数学模型。将证候指标三碘甲腺原氨酸（T3）和四碘甲腺原氨酸（T4）和促甲状腺激素（TSH），睾酮（T），促卵泡刺激素（FSH），黄体生成素（LH）作为决策属性集D，而属性值是由动物实验获得的原始数据形成。经过对各属性集进行属性约简，应用粗糙集建立预测模型，最终得到优化药方，并通过相关实验进行了验证，误差值基本保持在10%左右，说明粗糙集对于中药复方的优化是可行的。见表2。

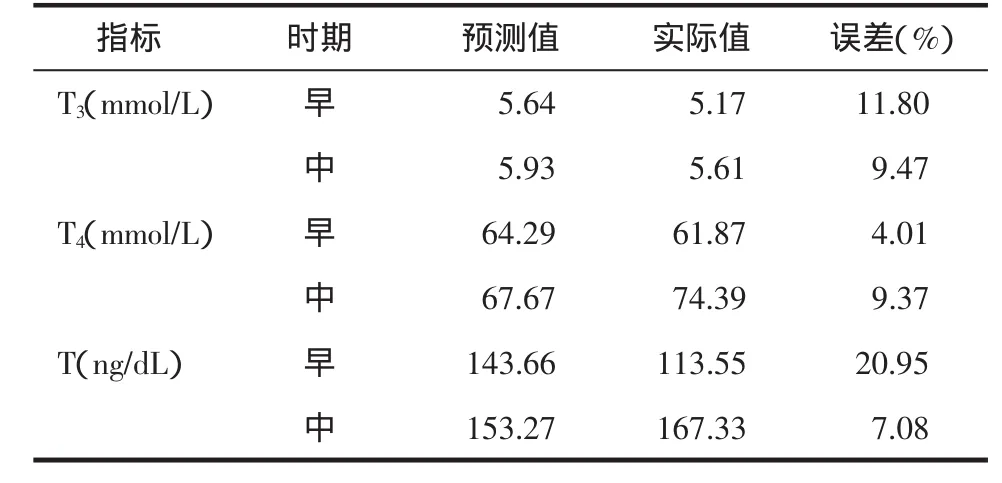
表2 粗糙集模型结果及误差（取5只得平均值）

4 熵理论分析方法

杨洪军等[10]以《中药方剂大辞典》中的中风等主治方剂为例，在复杂系统分划的熵方法的基础上提出的改进的关联度系数的分析方法，对比分析两个随机变量Xi和Xj之间的关联度系数ij如公式（9）所示：

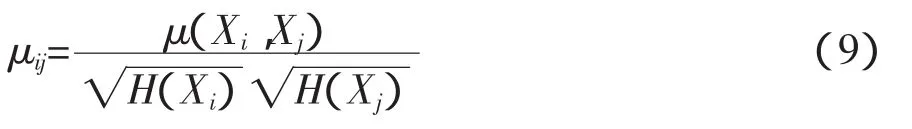
得出500首方剂中234种中药每两味之间的系数，如表3所示。

表3 药对关联度系数表 对

其中具有中医理论依据的组合共185对。这种系统的熵的理论分析方法开辟了一条中医药分析方法的新途径，尤其在中药药对关系的探讨上有较明显的指导作用，值得借鉴。

王师菡等[11]以2004—2007年间中国中医科学院广安门医院心内科的名老中医药专家的100例冠心病心绞痛医案的319则中药处方为研究对象，在建立的数据库中使用逻辑二值变量赋值方法，将某一方剂中所涉及的中药均赋予值1，其他自动赋值0。采用广义信息熵关联度法，运用信息熵关联度μ（Xi，Xj）＝H（Xi）＋H（Xj）－H（Xi，Xj）对此319首中药处方进行分析，得到如下的药对关系，见表4。

表4 药对熵关联度表 对

其中重点指出系数在0.5以上的药对主要都是名老中药专家最常用的，符合中医理论和临床用药经验。此方法能够提高对中医名方的规律认识，有利于对中医方剂更好的理解与探索。

唐仕欢等[12]为解决熵的关联度μ（Xi，Xj）只能是非负值，不能区分变量正、负相关的差别，而将关联度系数进行了改写，得到改进的动态关联度系数如公式（10）所示：

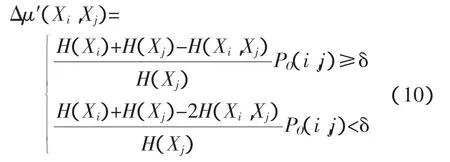
经过运算分析会得到两个正相关的亲密变量，聚成一堆的3个正相关变量，以此类推根据这种复杂系统熵聚类方法可筛选出多元的中药核心组合，作为专家判断和确立候选处方的依据，并以感冒方剂为例验证了此法的可行性，值得借鉴、推广。

5 结语

5．1 方法多样，各有所长 中医药学理论中充满了数学语言和思维[13]，以上对中医方剂研究的各种数学方法在针对不同的研究领域都有一定的成效。

线性分析方法注重中药的定性、定量处理，使中药各药性、药效更直观[14]。函数分析方法将中药量效等传统中医理论数学概念化，提出了“相对药量”等概念和相关数学模型，增强了方剂中各中药的可比性。集合分析方法以中医理论为根本从宏观角度对中医方剂进行了研究，有效约简了中医方剂的分析过程，提高了中医方剂的研发速度[15]。而随着计算机技术的发展，熵方法对于挖掘医学研究中所得的大量数据间有价值的信息越来越显示出了自身优势[16]。熵理论的分析方法，在具体的方剂模型中对各中药的关联度等作了深入的研究，可以快速、准确筛选和发现供临床应用或中药新药研发的常用药对和核心组合，避免了个人经验的局限，是值得推广和研究的有效方法[17]。

5．2 采众家之长，交互融合，综合运用 通过以上对常用中医方剂内在规律的数学方法的分析、归纳，可以指导在运用数学思维对中医方剂内在规律进行研究时，应针对各种数学方法的不同特点综合运用[18]，采众家之长，系统深入地进行中医药内在数学规律的挖掘。

5．3 忌脱离中医传统知识，空谈数学理论 在系统进行中药有效成分分析研究的同时，应注意在中医理论指导下中药本身的性味归经等特性[19]，忌脱离中医药传统理论[20]，单纯从数学角度进行数据挖掘，从而失去了研究的实际意义。

[1] 盛志刚，白 晶．中医方剂定量分析方法初探[J].中华中医药杂志，2007，22（5）：262－264．

[2] 颜素容，王 耘，乔延江．方剂药性特征的表述方法及其应用[J].北京中医药大学学报,2010，33（5）：297－299．

[3] 王文刚.基于量效的方剂分析法尝试[J].陕西中医学院学报，2011，34（6）：73－74．

[4] 任廷革，刘晓峰，高全泉，等．中医方剂功效定性和定量研究初探[J].中医药信息学,2007，14（6）：100－102.

[5] 高全泉，任廷革，刘晓峰，等．中医方剂药物相对药量改进计算模型[J].海南师范大学学报（自然科学版），2008，21（4）：362－366.

[6] 顾作林，袁同山，李 芳，等．中医方药量化研究中“相对药量”的数学模型体系[J].数学实践与认识，2010，40（9）：154－157.

[7] 李龙江，白 雪．基于粗糙集理论的复方拆方研究[J].太原师范学院学报（自然科学版）,2005，4（4）：30－322．

[8] 于润桥，杨琳瑜，王建红，等.基于粗糙集理论的中医方证系统模型的建立[J].辽宁中医药大学学报，2007，9（1）：5－7．

[9] 危 荃，于润桥，王建红，等.基于粗糙集的复方右归丸优化与验证[J].辽宁中医杂志,2008，36（8）：1123－1125．

[10]杨洪军，赵亚丽，唐仕欢，等．基于熵方法分析中风病方剂中药物之间的关联度[J].中国中医基础医学杂志，2005，11（9）：706－709.

[11]王师菡，王 阶，何庆勇，等．基于信息熵法提取名老中医治疗冠心病心绞痛的药对[J].中华中医药学刊，2008，26（10）：2150－2152．

[12]唐仕欢，陈建新，杨洪军，等．基于复杂系统熵聚类方法的中药新药处方发现研究思路[J].世界科学技术·中医药现代化，2009，11（2）：225－228．

[13]孟庆刚，郭书文．如何将数学方法应用于现代中医药学研究[J].中国中医药信息杂志，2000，7（8）：21－22，48．

[14]王 阶，王永炎，杨 戈．中药方剂配伍理论研究方法和模式[J].中国中药杂志，2005，30（1）：6－11．

[15]李小梅，李续娥．数学方法在中医药研究中的应用[J].中华中医药学刊，2007，25（10）：2103－2104.

[16]王天芳，李志更，吴秀艳，等．基于信息熵关联度系数法的慢性肾功能衰竭中医症状组合的探索[J].北京中医药大学学报，2010，33（7）：493－495，499.

[17]唐仕欢，陈建新，杨洪军，等．基于复杂系统熵方法的抗肺痨方剂组方规律研究[J].中国中药杂志，2010，35（24）：3368－3370.

[18]王 阶，郭丽丽，王永炎．中药方剂有效成（组）分配伍研究[J].中国中药杂志，2006，31（1）：5－9.

[19]王益民，曹红梅，张皓楠，等．中医工程学研究现状与思考[J].天津中医药大学学报，2009，28（2）：108－109．

[20]吕佳萍，孙向荣，周介南．数学方法在中药研究方面的应用[J].时珍国医国药，2011，22（3）：713－714．

R22

A

1673－9043（2012）01－0061-04

300193 天津中医药大学（张 砚，王益民，刘 霞）300074 天津中德职业技术学院（刘 霞）

张 砚（1980-），男，助理研究员，博士在读，主要从事计算机技术辅助人事管理工作和计算机技术辅助中医工程学研究。

王益民。

2011-12-08）