＊带分数Brown运动的非线性随机两种群系统的最优控制

梁翠翠，张启敏

（宁夏大学 数学计算机学院，宁夏 银川 750021）

＊带分数Brown运动的非线性随机两种群系统的最优控制

梁翠翠，张启敏

（宁夏大学 数学计算机学院，宁夏 银川 750021）

讨论带分数Brown运动的非线性随机两种群系统的最优控制问题，得到了当外界环境对种群系统产生影响的条件下，控制为最优的必要条件，所得到的结论是已有确定性种群系统的扩展.

非线性；两种群；最优控制；分数布朗运动

0 引言

考虑如下随机两种群系统（P）

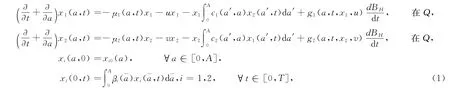
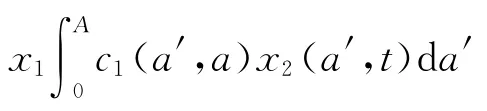
分数Brown运动具有自相似性和长记忆性，由于种群系统也具有长记忆性，即种群系统将来的状态不仅仅只跟现在的状态有关，跟过去的状态也是有联系的，不是相互独立的.所以考虑带分数Brown运动随机种群系统的有关问题更符合实际.关于分数Brown运动大量文献对其进行了研究，例如：文献［1］讨论了分数Brown运动的定义，自相似性，连续性，可微性及其应用.由于分数Brown运动不是半鞅，一般的Ito积分理论不再适用，文献［2］根据随机变分原理给出了带分数Brown运动函数的Ito公式.文献［3］讨论了线性和非线性带分数Brown运动倒向随机微分方程解的存在性和唯一性.文献［4］研究了短期分数Brown运动环境中最优投资组合选择问题，运用Hamilton函数和Lagrange算子将随机最优控制问题转化为非随机优化问题，根据确定最优控制原理得到了最优策略的显示解.文献［5］讨论了分数Brown运动与Hurst指数之间的关系，给出了当Hurst指数取不同值时分数Brown运动相应的性质.文献［6］研究了半线性随机加热方程描述的系统最优控制极大值原理的充分性，结论用于解决最优收获问题.文献［7］讨论了介于0＜H＜1任意参数分数布朗运动的Ito公式.文献［8］根据偏微分方程和分数Ito公式的解得到了带分数Brown运动的线性倒向随机微分方程的显式解.文献［9］讨论了带分数Brown运动的随机极大值原理.文献［10］研究了用Riemann－Liouville分数Brown运动在生物系统考虑随机性，讨论了带分数Brown运动的两个种群的最优管理，运用Lagrange乘子法将随机问题转化为非随机问题，根据确定系统最优控制变分原理得到最优解.

1 预备知识

定义1.1 （Ω，F，P）是概率空间，H为 Hurst参数，0＜H＜1，随机过程｛B（t，H），t≥0｝定义在该概率空间上为H阶分数布朗运动（f Bm）H具有下列性质：

（1）P｛B（0，H）＝H｝＝1，

（2）对任意的t≥0，B（t，H）是F可测随机变量且E［B（t，H）］＝0，

（3）对任意的t≥0，

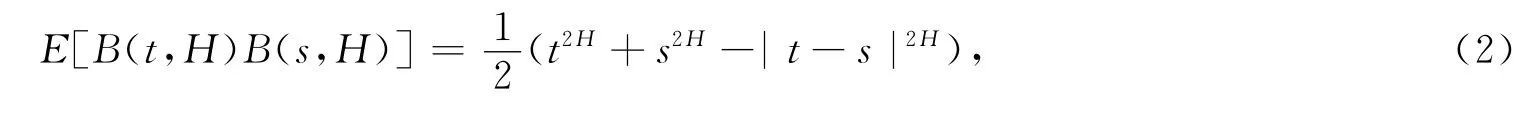
根据文献［11－12］，对分数布朗运动（f Bm）H的进一步讨论如下.

（1）方程（2）可以由下列等式得到：

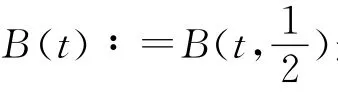
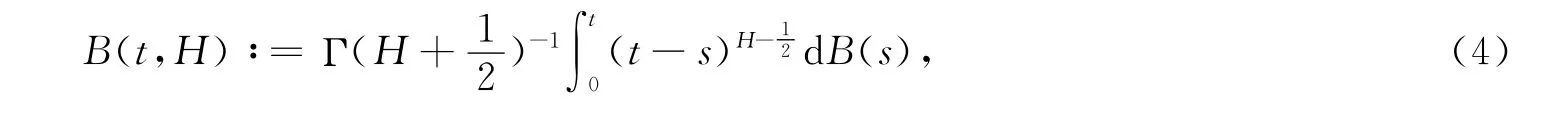
Γ是gamma函数.

（3）引用 Maruyama记法（文献［12］）有定义1.2 设f表示连续函数，则它的H阶分数导数定义为：

2 主要结果

证明 根据文献［14］知：控制（¯u，¯v）∈U为问题1.1最优控制的充分条件是对任意的（u，v）∈U下式成立

3 结束语

由于种群系统经常受到外部环境的影响，具有随机扰动的种群系统模型便成了人们讨论的热点.然而，对于种群系统，大量文献只针对确定系统进行研究，并未考虑随机因素的影响.所以本文讨论了带分数Brown运动的非线性随机两种群系统的最优控制问题，给出了控制为最优的必要条件.本文的结论是确定性种群系统的扩展.

［1］ Benoit B.Mandelbrot，John W.Van Ness.Fractional Brownian Motion，Fractional Noises and Applications［J］.SIAMReview，1968，10（4）：422－437.

［2］ Decreeusefond，A SÜStunel.Stochastic Analysis of the Fractional Brownian Motion［J］.PotentialAnalysis，1990，10：177－214.

［3］ Hu Yao－zhong，Peng Shi－ge.Backward Stochastic Differential Equation Driven by Fractional Brownian Motion［J］.SIAM JControlOptim，2009，48（3）：1675－1700.

［4］ Gao Jian－wei.Optimal Portfolio Selection Under the Short－Range Fractional Brownian Motion［C］／／International Conference on Computational Intelligence and natural Computing，2009：433－436.

［5］ 牛奉高，刘维奇.分数布朗运动与 Hurst指数的关系研究［J］.山西大学学报：自然科学版，2010，33（3）：380－383.

［6］ Bernt Ksendal.Optimal Control of Stochastic Partial Differential Equations［J］.Stochastic Analysis and Applications，2005，23：168－179.

［7］ Christian Bender.An Ito Formula for Generalized Functional of Fractional Brownian Motions with Arbitrary Hurst Parameter［J］.StochasticProcessesandtheirApplications，2003，104：81－106.

［8］ Christian Bender.Explicit Solutions of a class of Linear Fractional BSDEs［J］.SystemsandControlLetters，2005，54：671－680.

［9］ Francesca Biagini，Hu Yao－zhong，Bernt Ksendal，Agues Sulem.A Stochastic Maximum Principle for Processes Driven by Fractional Brownian Motion［J］.StochasticProcessesandtheirApplications，2002，100：233－253.

［10］ Guy Jumarie.New Stochastic Fractional Models for Malthusian Growth，the Poissonian Birth Process and Optimal Management of Populations［J］.MathematicalandComputerModelling，2006，44：231－254.

［11］ Guy Jumarie.Fractional Master Equation：non－standard Analysis and Liouville－Riemann Derivative［J］.Chaos，Solitons andFractals，2001，12：2577－2587.

［12］ Guy Jumarie.On the Representation of Fractional Brownian Motion as an Integral with Respect to（dt）a［J］.Applied MathematicsLetters，2005，18：739－748.

［13］ Guy Jumarie.Fractional Brownian Motions Via Random Walk in the Complex Plane and Via Fractional Derivative.Comparison and Further Results on Their Fokker－Planck Equations［J］.Chaos，SolitonsandFractals，2004，22：907－925.

［14］ Abel Cadenils.A Stochastic Maximum Principle for Systems with Jumps with Applications to Finance［J］.Systemsand ControlLetters，2002，47：433－444.

Optimal Control of Nonlinear Stochastic Two
Population Systems with Fractional Brownian Motion

LIANG Cui－cui，ZHANG Qi－min
（SchoolofMathematicsandComputer，NingxiaUniversity，Yinchuan750021，China）

The optimal control of nonlinear stochastic two population systems driven by fractional brownian motion is discussed.When the external environment affects the system，the necessary conditions for the optimization was made clear，obtained the conclusion was the expansion of definite population system.

nonlinear；two systems；optimal control；fractional Brownian motion

O175.12

A

0253－2395（2012）04－0595－08＊

2011－07－05；

2011－10－26

国家自然科学基金（11061024）

梁翠翠（1988－），女，硕士，主要研究方向：运筹学与控制论.E－mail：liangcui4567＠163.com