＊ 等变形压加载下单晶铝fcc－bcc相变的分子动力学模拟

郭钰，何凯，李莉，梁九卿

（山西大学 理论物理研究所，山西 太原 030006）

＊等变形压加载下单晶铝fcc－bcc相变的分子动力学模拟

郭钰，何凯，李莉＊，梁九卿

（山西大学 理论物理研究所，山西 太原 030006）

采用EAM势，利用分子动力学方法模拟了单晶铝在高速率等变形压加载条件下的fcc－bcc的结构相变.模拟结果表明，在等变形压加载条件下，单晶铝在加压至270 GPa左右，体积缩小至0.55V0时，由面心立方结构转变为体心立方结构.这一结果与第一原理计算的结果大致符合.

分子动力学；金属铝；等变形压加载；结构相变

0 引言

许多金属在高压条件下会发生结构相变，使得材料的宏观性质发生变化，因此研究金属高压下的行为一直是一个研究热点，这其中不乏对铝高压行为的研究［1－7］.多年来，人们用不同的理论方法计算了铝在高压下可能存在的相变及所对应的相变临界压力值.计算结果普遍认为铝在高压下存在fcc－hcp－bcc或fcc－bcc的相变，但用不同的方法得到的相变临界压力却大不相同.1981年，Moriarty和Mc Mahan［1］分别用GPT（the generalized pseudo potentialtechnique）与 LMTO（all－electronlinear muffin－tin－orbital method）两种方法对铝的面心晶格结构（fcc）、六角密堆积结构（hcp）和体心晶格结构（bcc）进行计算.用GPT得到fcc－hcp相变的压力为360 GPa，而用LMTO得到fcc－hcp相变的压强为120 GPa.还有一些文献［2－3］采用其它方法计算fcc－hcp的相变压力，计算得出的临界压力大约从170 GPa到220 GPa.Mishrab和Chaturvedi则认为铝在275 GPa左右会发生由fcc－bcc的相变［4］.在实验上，Greene［6］等人用 DAC（diamond－anvil－cell）方法对铝进行了高压实验，实验中压力最高达到219 GPa，但在铝中没有发现任何形式的结构转变.2006年，Akahama［7］等人将压力提高至330 GPa后发现铝在（217±10）GPa时发生了fcc－hcp相变.这是人们第一次在实验中观测到铝的高压相变，并且实验结果与一些理论计算结果符合的很好，这在很大程度上激发了人们对铝高压相变的研究热情.

近年来，由于计算机的快速发展和计算机硬件性能的提高，分子动力学（MD）得以大力发展，它在探测原子尺度细节上所具有的独特优势，使其在科学研究中得到广泛的应用.分子动力学可以被用来研究晶体微观机制的动力学现象，目前已成功地模拟了相变、孪晶、位错发射［8－9］等现象.MD在模拟金属铝的形变过程中也取得了巨大的成功，例如，Yamokov［10］等人模拟了纳米晶体铝的形变过程，得到了很多有价值的结论.本文将利用MD来模拟铝在高压下的结构转变.

1 模拟方法

原子间相互作用势是MD模拟的重要物理基础，而嵌入势函数（EAM）可以很好地描述金属及合金中原子间的相互作用，在金属及合金的结构、物性等研究中被广泛应用.本文所采用的势函数的具体形式及参数由Adams等人［11］给出，Adams对EAM势参数进行了拟合，拟合结果表示在表1中（P676），从表1中可以看出，该工作的拟合结果与已有的大量实验数据吻合的很好.

表1 Adams拟合的势函数计算所得数据与已有实验数据的比较Table 1 EAM potention parameter of Adams compared with experimental data

模拟中用到的样品由256 000个原子组成，样品的晶格常数a＝0.403 5 nm，长为x＝80a，宽为y＝80a，高为z＝80a.模拟中在三个方向均采用周期性边界条件.加载前，用速度标定法［12］控制样本的初始温度为50 K，通过调节晶格常数使初始压强为0 Pa.模拟中通过逐步缩小三个晶向的晶格常数实现沿［100］、［010］、［001］三晶向的等变形压加载.在计算中对牛顿方程的积分采用 Verlet algorithm［13］方法，时间步长是0.001 ps，总模拟时间为100 ps.

2 结果与讨论

2.1 铝的高压相变计算

图1、图2是通过计算fcc、hcp和bcc结构铝在不同压力下各相原子总能量和原子体积的关系得到的冷能曲线.通过这一曲线我们可以看出随着压力的上升，铝在高压下可能存在两种相变，即fcc－hcp和fcc－bcc的相变，这两种相变所对应的压力大约为61 GPa和210 GPa.与其它理论计算相比，这一相变转变压力要偏低一些.

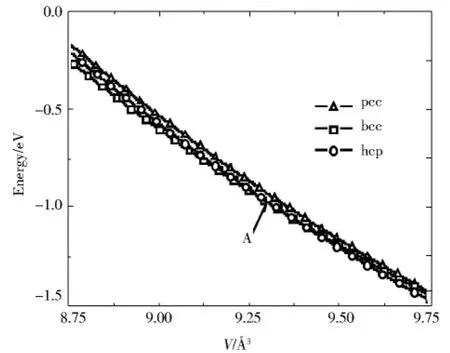
图1 冷能曲线Fig.1 Curves of cold energy

图2 冷能曲线Fig.2 Curves of cold energy

2.2 加载过程中压强和温度的变化

图3表示在加载过程中样品压强随应变率ε的改变，其中ε＝（V0－V）／V0，V0表示样品的初始体积.图4是加载过程中样品温度随应变率ε的变化.从图3、图4上可以清楚的看出，在加载的初始阶段，两曲线均近似呈线性关系，当ε接近0.45时，这种线性关系被破坏，在两曲线上出现突变点，在后面的分析中，我们可以清晰地看到突变点是由fcc－bcc的相变引起，而不是由于基于位错发射的塑性变形引起的.当ε超过0.45时温度会迅速地升高，这是因为相变时相变潜热的释放造成的.在本文的加载条件下，金属铝从fcc－bcc相变的临界压强大约是270 GPa，这一结果与第一性原理的计算结果吻合的较好.

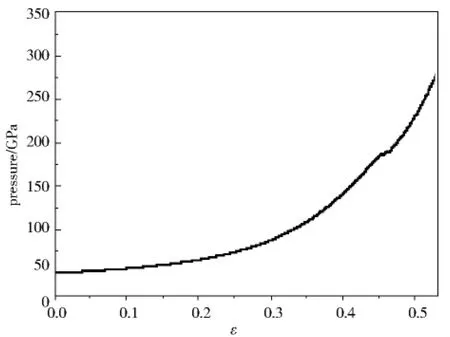
图3 加载过程中压强随应变率ε的变化Fig.3 Pressure as a function of strainεin loading process

图4 加载过程中温度随应变率ε的变化Fig.4 Temperature as a function of strainεin loading process

2.3 径向分布函数（RDF）

为了进一步证实相变的发生，我们在模拟中计算了样品在不同应变率的径向分布函数.图5是加载过程中不同的ε值时样品的径向分布函数图.其中ε的变化范围为0～0.54.可以看到，在ε＝0时，样品为典型的fcc结构，并且由于温度效应，所有峰有一定的展宽.

由于加载过程三个晶向的晶格常数不断被压缩，因此曲线上表示第一近邻原子的峰在加载过程中都向左移动.当ε＝0.45时，相变开始发生，从图中可以看到，此时RDF曲线的各个峰开始变的不是很清晰，说明此时样品开始经历一个结构重组的过程，旧相开始消失，同时新相开始产生.而当ε＝0.46时，样品的第一个峰已经出现了明显的劈裂，代表bcc相的一些典型的峰已经开始出现.随着应变率的增加，这一变化越来越明显，在应变率达到0.54时，RDF曲线已经代表了典型的bcc结构，也就是说，此时fcc－bcc的相变已经完成，最终样品以bcc相为主要结构.

2.4 加载过程中相变特征的分析

为了分析相变过程中新相的形成特点，我们用键对分析的方法来识别样品中的原子是以fcc，bcc相和晶界中的哪一种状态存在.图6（P678）是样品在不同应变率时的结构图及对应的截面图.其中，fcc相、晶界原子和bcc相分别以浅灰、白色和灰黑色原子所表示.可以看到，在加载初期，样品结构为典型的fcc结构.当应变率增加至0.449时，样品中开始有bcc相出现（图6（b）和（e））.这一现象说明样品在这一应变率下正经历由fcc－bcc的结构相变过程，原子的排列方式正经历一个重构形成新相的过程.当应变率增大至0.469时，从图6（c）和（g）中可以看到，bcc结构已经大量出现在整个样品中了.并且值得注意的是，在相变完成后，bcc相的晶界界面以3个界面为主，它们是（011），（101）和（－110）界面（图6（d）和（h））.

图5 加载过程中Al在不同应变下的径向分布函数Fig.5 RDFs of the sample under different strainsεin the loading process

图6 加载过程中样品在不同应变下的结构图及对应的截面图.fcc结构、晶界原子、bcc结构分别以浅灰色、白色、灰黑色原子表示Fig.6 Morphology evolution of the sample structure in the loading process.The panels show snapshots at different ε.Grayish atoms，white atoms and deep gray atoms stand for the fcc phase，grain boundaries and bcc phase，respectively

3 结论

本文采用EAM嵌入势，用分子动力学方法，模拟了单晶铝在高应变率等变形压加载条件下的相变过程.结果表明，单晶铝在这一加载条件下会发生fcc－bcc的相变.相变的临界压强约为270 GPa，体积缩小至0.54V0.这一计算结果与第一原理的计算结果大致吻合.相变结束后，bcc相的晶界界面以3个界面为主，它们是（011），（101）和（－110）界面.

［1］ Moriarty J A，Mc Mahan A K.High－Pressure Structural Phase Transitions in Na，Mg，and Al［J］.PhysRevLett，1982，48：809－812.

［2］ Lam P K，Cohen M L.Calculation of High－pressure Phases of Al［J］.PhysRevB，1983，27：5986－5991.

［3］ Boettger J C，Trickey S B.High－precision Calculation of the Equation of State and Crystallographic Phase Stability for A－luminum ［J］.PhysRevB，1996，53：3007－3012.

［4］ Mishra V，Chaturvedi S.Theoretical Study of FCC－HCP Phase Coexistence and Phase Stability in Al by FP－LAPW Method with GGA for Exchange and Correlation［J］.PhysicaB，2007，393：278－284.

［5］ 邵建立，何安民，秦承森，等.一维应变加载下单晶铁结构转变的微观研究 ［J］.物理学报，2009，58：5610－5617.

［6］ Green R G，Luo H，Ruoff A L.Al as a Simple Solid：High Pressure Study to 220 GPa（2.2 Mbar）［J］.PhysRevLett，1994，73：2075－2078.

［7］ Akahama Y，Nishimura M，Kinoshita K，etal.Evidence of a fcc－hcp Transition in Aluminum at Multimegabar Pressure［J］.PhysRevLett，2006，96：045505.

［8］ Li L，Shao J L，Duan S Q，etal.Atomistic Simulation of the fcc－hcp Transition in Single－crystal Al Under Uniaxial Loading［J］.NewJPhys，2010，12：033011.

［9］ Yamakov V，Wolf D，Phillpot S R，etal.Deformation Twinning in Nanocrystalline Al by Molecular－dynamics Simulation［J］.ActaMater，2002，50：5005－5020.

［10］ Yamakov V，Wolf D，Phillpot S R，etal.Dislocation Processes in the Deformation of Nanocrystalline Aluminium by Molecular－dynamics Simulation［J］.NatMater，2002，1：45－49.

［11］ Ercolessi F，Adams J B.Interatomic Potentials from First－Principles Calculations：the Force－Matching Method［J］.EurophysLett，1994，26：583－588.

［12］ Hoffmann K H.Computational Physics［M］.Berlin：Springer，1996：268.

［13］ Swope W C，Andersen H C，Berens P H，etal.A Computer Simulation Method for the Calculation of Equilibrium Constants for the Formation of Physical Clusters of Molecules：Application to Small Water Clusters［J］.JChemPhys，1982，76：637－649.

Atomistic Simulation of Fcc－bcc Phase Transition in Single Crystal Al Under Uniform Deformation Compression

GUO Yu，HE Kai，LI Li，LIANG Jiu－qing
（InstituteofTheoreticalPhysics，ShanxiUniversity，Taiyuan030006，China）

By molecular dynamics simulations employing an embedded atom method potential，we simulate structural transformations in single crystal Al caused by high rate uniform strain loading.The simulations show that the phase transition takes place at about 270 GPa，corresponding to the reduced volume of 0.55V0，in reasonable agreement with the calculated value through density functional theory.

molecular dynamics simulations；single crystal Al；uniform strain loading；phase transition

O411

A

0253－2395（2012）04－0675－05＊

2011－11－07；

2012－03－05

国家基础科学人才培养基金（J1103210）

郭钰（1987－），女，山西长治人，硕士生，研究方向为理论物理.＊通讯联系人：E－mail：sxu＿lili＠163.com