＊ 标准模型下基于身份的盲签名方案

汤鹏志，李彪，邓俊蕾，徐雷

（1.华东交通大学 基础科学学院，江西 南昌 330013；2.武警九江市消防支队 德安大队，江西 九江 330400）

＊标准模型下基于身份的盲签名方案

汤鹏志1，李彪1，邓俊蕾1，徐雷2

（1.华东交通大学 基础科学学院，江西 南昌 330013；2.武警九江市消防支队 德安大队，江西 九江 330400）

由于随机预言模型实现过程存在安全缺陷，提出一种标准模型下基于身份的安全盲签名方案.方案中首先定义基于身份盲签名的安全模型；然后利用双线性对构建盲签名方案；最后，在标准模型下给出基于CDH假设的方案安全性证明.因此，在自适应选择消息和身份攻击下，该方案是安全的.

盲签名；标准模型；CDH－问题；基于身份密码；双线性对

0 引言

盲签名［1］的概念是Chaum在1982年提出的，它是一种具有特殊性质的数字签名.消息拥有者在不公布消息真实内容的情况下，获得消息签名者对真实消息的合法签名.基于身份的密码学方案［2］是由Shamir于1984年提出的，其主要观点是：使用用户唯一标识（如：姓名、IP地址、电子邮件地址等）作为公钥，私钥则由可信的密钥生成中心PKG（Private Key Generator）进行计算得到.结合盲签名和基于身份密码学，利用双线性对映射［3］，Zhang和Kim提出了基于身份的盲签名方案［4］.目前，不少研究者仍致力于基于身份的盲签名方案［5－6］的研究，但大多是在随机预言模型［7］下证明安全或者没有安全模型证明.然而随机预言机模型在实现过程中，仍存在安全隐患.而今，盲签名协议已经广泛应用在电子商务协议中，故在标准模型下证明盲签名安全性具有很好的应用前景.

自Waters于2005年首次提出标准模型下基于身份的高效密码方案［8］以来，便引来众多信息安全研究者的青睐，并陆续提出许多新的标准模型签名方案［9－12］.本文结合文献［8］思想，利用双线性对映射，提出一种基于身份的盲签名方案，并在标准模型下将协议的安全性规约至双线性群中的CDH问题假设，即方案在适应性选择消息和身份攻击下是不可伪造的.

1 基础知识

1.1 双线性对

假设｜G｜为群G的阶；＋是加群的运算；×是乘群的运算；n∈N＋；Z p为模p的剩余类整环；Z＊p是Z p可逆元集合.

定义1 设（G1，＋），（G2，×）分别是阶为p的循环加群和循环乘群.p为素数，g是G1的生成元.存在对映射：e：G1×G1→G2，如果对映射满足以下性质：

（1）双线性：对所有的a，b∈Z＊p，满足等式：e（g a，g b）＝e（g，g）ab；

（2）非退化性：e（g，g）≠ρ，其中ρ是G2的幺元.

（3）可计算性：存在有效算法计算e（g a，gb），则称该对映射e为双线性映射.

1.2 困难问题假定

定义2 CDH问题：假设素数p为群G的阶，g是G的生成元，若已知a，b∈RZ＊p和g a，gb∈G，计算g ab.

定义3 （ε，t）－CDH假设：在概率多项式时间t内，不存在任何算法以大于或等于ε的概率解决群G上的CDH问题.

2 基于身份的盲签名体制

2.1 体制定义

定义4 （IBBS签名体制）设基于身份的签名体制IBS＝｛ψ，φ，ξ，υ｝，则基于身份的盲签名体制为IBBS＝｛ψ，φ，ζξτ，υ｝

（1）系统建立（Setup）：系统参数设置算法ψ，其输入一个安全参数1k，输出系统参数Params和主密钥msk（其中params，msk←ψ（1k）），密钥生成中心（PKG）公开系统参数Params，并秘密保存系统主密钥msk.

（2）私钥提取（Exctract）：PKG运行概率多项式密钥生成算法φ，输入用户身份IDs，输出相应身份的密钥：s←φ（IDs，msk，Params）.首先PKG通过安全信道将密钥发送给用户，然后用户验证私钥的正确性.

（3）盲签名（Blind Sign）：盲签名算法（ζξτ）是签名者和用户之间执行的概率多项式时间交互协议.首先，用户运行盲化算法（ζ），输入消息M，输出M盲化后的信息σu←ζ（M），将σu发送给签名者.然后签名者运行签名算法（ξ），输入密钥s和σu，输出σs←ξ（σu，s），将σs返回给用户.最后用户运行去盲算法（τ），输入σs，输出消息 M 的签名信息σ←τ（σs）.

（4）验证（Verify）：给定系统参数Params、签名者身份IDs、消息 M和签名σ，确定性验证算法（υ）输出盲签名σ的合法性Legality＝υ（Params，IDs，M，σ）.若盲签名有效，输出true；否则输出false.

2.2 安全模型

定义5 在满足盲性的情况下，如果不存在任何多项式有界的攻击者，以ε的优势赢得挑战者C和攻击者A之间的攻击游戏，则称基于身份的盲签名方案是自适应性选择消息和身份攻击下存在不可伪造性的安全模型.攻击游戏如下所示：

（1）准备阶段（Setup）：挑战者运行系统参数设置算法ψ，得到系统参数Params和主密钥msk.并发送给攻击者系统参数Params，保密主密钥msk.

（2）询问阶段（Queries）：攻击者自适应性的向挑战者提出一系列密钥询问和盲签名询问.

密钥询问（Extract Queries）：攻击者能够获取任何身份IDsi的私钥si.挑战者运行φ（IDsi，msk，Params）来进行响应，并将私钥si发送给攻击者.

盲签名询问（Blind Sign Queries）：攻击者能够获取任意身份IDsi对消息M的签名σ.

① 攻击者通过运行ζ（M），获取消息的盲化信息σu，并将其发送给挑战者.

② 挑战者运行φ（IDsi，msk，Params），获取身份IDsi的私钥si；然后通过运行ξ（σu，si）来获取σs，并将其发送给攻击者.

③ 攻击者运行τ（σs），获取签名信息σ.

（3）伪造（Forgery）：攻击者输出消息M＊、身份ID＊s、签名σ＊.若以下3个条件成立，则攻击成功.

①υ（Params，ID＊s，M＊，σ＊）＝true；

②攻击者未对身份ID＊s做密钥询问；

③攻击者未对（ID＊s，M＊）做盲签名询问.

如果攻击者成功伪造签名，游戏返回true，否则返回false.在上述游戏中攻击者获胜的优势定义为：advIBBSA（1k）＝｜Pr［φ（g，g a，gb）＝g ab］－1／2｜.

定义6 对于基于身份的盲签名方案，如果攻击者在t时间内，做qe次密钥询问和q s次签名询问，不能以ε的概率获胜上述游戏，则称方案是（ε，t，qe，qs）安全的.

3 基于身份的盲签名方案

假设签名者身份和待签名消息分别是IDs和M，可利用抗碰撞的安全哈希函数将签名者身份和消息分别映射到长为nu，nm的比特串，H u：｛0，1｝＊→｛0，1｝nu，H m：｛0，1｝＊→｛0，1｝nm.

（3）盲签名生成（Blind Sign）：用户User，签名者Signer，消息M按照如下步骤生成盲签名：

4 方案分析

4.1 正确性分析

（1）用户私钥生成阶段

（2）签名去盲阶段

（3）验证阶段

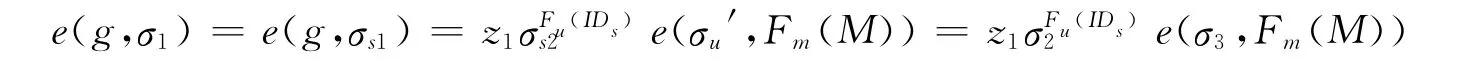
4.2 安全性分析

基于身份的盲签名方案需要满足盲性和不可伪造性.在盲签名过程中，签名者可以获知（M，σ，σu，σs）；因为签名者无法得知盲化因子γ，签名者无法知道消息的真实内容，因此本方案已经具备盲性.下面在标准模型下，证明本方案仍具有不可伪造性.

证明 假设签名伪造者能够构造挑战者解决CDH问题.给定G中元素g，g a，gb，目标是计算g ab，伪造者构造算法φ，充当挑战者的身份，模拟挑战者与攻击者之间的攻击游戏.

为便于分析，定义下列函数：

算法中的时间复杂度取决于密钥询问和盲签名询问的运算量.在询问过程中，需要消耗时间较大的是群G中乘法运算、指数运算和双线性对运算.由于密钥询问和盲签名询问分别需要O（1），O（nm）次群G中的乘法运算和O（1），O（1）次群G中的指数运算，但仅有密钥询问需要O（1）次双线对运算.因此，算法φ的时间复杂度为：t′＝t＋O（（qe＋nmqs）ρ＋（qe＋qs）τ＋qeϑ）.

4.3 效率分析

在盲签名阶段，用户最多需要进行nm＋3次（平均nm／2＋3次）群G中乘法运算、3次群G中的指数运算和1次双线性对运算；签名者需要进行1次群G中乘法运算和2次群G中的指数运算.在签名的验证阶段，验证者最多需要进行nm＋3次（平均nm／2＋3次）群G中乘法运算、1次群G中指数运算和1次双线性对运算.因为e（g1，g2）的值是预先计算出来的，故至少减少了1次双线性对运算和1次群G中的指数运算.

5 结束语

现有的基于身份的盲签名方案，其安全性大部分是没有安全模型证明或者在随机预言机模型下证明.本文建立能抵抗适应性选择消息和身份攻击下的安全模型，提出基于身份的盲签名方案.在标准模型下，将方案的不可伪造性规约至双线性群中的CDH问题假设.本方案不但满足盲签名的特性，并且拥有很高的安全性，在电子商务中具有较好的应用前景.

［1］ Chaum D.Blind Signatures for Untraceable Payments［C］／／Advances in Cryptology－Crypto′82，LNCS，1982：199－203.

［2］ Shamir A.Indentity－based Cryptosystems and Signature Scheme［C］／／Proceedings of Crypto′84，Berlin：Spring－Verlag，1984：47－53.

［3］ Boneh D，Franklin M.Identity－based Encryption from the Weil Pairing［C］／／Proceedings of Crypto′2001，Berlin：Springer－Verlag，2001：213－229.

［4］ Zhang F，Kim K.Efficient ID－based Blind Signature and Proxy Signature from Bilinear Pairings［C］／／Information Security and Privacy，Heidelberg：Springer－Verlag，2003：312－323.

［5］ 褚万霞，张建中.高效的基于身份的盲签名方案［J］.计算机工程与应用，2010，46（36）：112－113.

［6］ 李明祥，郑艳娟，安文广.一种高效的基于身份的部分盲签名方案［J］.计算机应用研究，2010，27（11）：4299－4303.

［7］ Bellare M，Rogoway P.Random Oracles are Practical：A Paradigm for Designing Efficient Protocols［C］／／Proceedings of the First Conference on Computer and Communications Security，New York：ACM，1993：62－73.

［8］ Waters B.Efficient Identity－based Encryption Without Random Oracles［C］／／Proceedings of Eurocrypt′2005，Berlin：Springer－Verlag，2005：114－127.

［9］ 李继国，姜平进.标准模型下可证安全的基于身份的高效签名方案［J］.计算机学报，2009，32（11）：2131－2136.

［10］ 王志伟，张伟.标准模型下基于因子分解问题的短签名［J］.通讯学报，2011，32（5）：78－81.

［11］ Hwang Y H，Liu J K，Chow S S M.Certificateless Public Key Encryption Secure Against Malicious KGC Attacks in the Standard Model［J］.JournalofUniversalComputerScience，2008，14（3）：463－480.

［12］ Boneh D，Boyen X.Efficient Selective Identity－based Encryption Without Random Oracles［J］.JournalofCryptology，2011，24（4）：659－693.

Identity－based Blind Signature Scheme Based on the Standard Model

TANG Peng－zhi1，LI Biao1，DENG Jun－lei1，XU Lei2
（1.SchoolofBasicScience，EastChinaJiaotongUniversity，Nanchang330013，China；
2.DeanContingent，JiujiangFireproofofChineseArmedPoliceForce，Jiujiang330400，China）

An identity－based secure blind signature scheme based on the standard model was introduced，because the implementation process of random oracle model presenced security defect.First，the security model of identity－based blind signatures was delimited；second，blind signatures was proposed by bilinear pairing；finally，the proof of scheme’s security was given in the standard model，which based on the Computational Diffie－Hellman assumption.Therefore，the scheme is security under adaptive chosen message and identity attacks.

standard model；CDH－problem；blind signature；identity－based cryptography；bilinear pairing

TP309

A

2012－03－05；

2012－06－03

国家自然科学基金（11061014）；江西省教育厅青年科学基金（GJJ10129）；江西省教育厅科研项目（GJJ10708）

汤鹏志（1961－），男，江西九江人，硕士，教授，硕士生导师，主要研究方向：信息系统及其安全.E－mail：nctpz＠126.com

0253－2395（2012）04－0648－06