度、半径约束最小生成树问题及其算法
2012-01-08冯祖针杨建强
石 磊,冯祖针,杨建强,龙 瑶
(红河学院数学学院,云南蒙自 661100)
度、半径约束最小生成树问题及其算法
石 磊,冯祖针,杨建强,龙 瑶
(红河学院数学学院,云南蒙自 661100)
提出了度、半径约束最小生成树问题,证明了该问题是NP-完全的.建立了该问题的数学规划模型.进一步给出了快速启发式求解算法,并分析了该算法的时间复杂性.分析和实例实验表明该算法具有良好的效果.
最小生成树问题;启发式算法;度约束;半径约束
最小生成树(Minimum Spanning Tree,简记为MST)[1]问题是网络中的一个经典问题,被广泛应用于网络优化问题中,如运输问题、网络路由选择、分布式系统、预测与决策[2]等.
MST问题的各种变形问题受到普遍的重视和研究.文献[3]对MST问题中的各节点加上一定的限制,得其一变形问题为度约束最小生成树(Degree-Constrained Minimum Spanning Tree,简记为DCMST)问题.文献[4]研究了图的每条边含有多个权值的多目标最小生成树(Multi-Criteria Minimum Spanning Tree,简记为MCMST)问题.单数据源节点的网络通信中与生成树相关的路由问题的研究通常为两个主要方面:网络综合性能最优化[5-6],归结为度约束最小生成树问题;网络中源节点到其他各节点的最大延迟最小化[7-8],归结为度约束最小半径生成树问题.上述MST变形问题都是NP-完全的.本文提出度、半径约束最小生成树(Degree-Constrained,Radius-Constrained Minimum Spanning Tree,简记为DCRCMST)问题,此问题综合考虑了上述网络路由研究所考虑的两个方面,因此有一定的实用价值.
1 问题描述和模型
设G=(vs,V,E,D,W)是无向网络,集合V的元素称为节点,记为vi,其中,vs为V中唯一的根节点,简称根,且|V|=n;集合E的元素称为边,(vi,vj)表示端点为vi和vj的边,且|E|=m;∀vi∈V,对应一个度约束值dmax(vi)∈N,称为度约束,D={dmax(vi)|vi∈V};∀(vi,vj)∈E,对应一个非负权值wij或w(vi,vj),称为长度或代价,W={wij|(vi,vj)∈E}.设wij为正整数.

定义2 度、半径约束最小生成树(DCRCMST)问题可以描述为寻找G的一个最小生成树T,满足当前节点的度dT(vi)≤dmax(vi)(∀vi∈T)和树的半径rad(T)≤Δmax(Δmax为半径约束值).取dmax(vi)和Δmax为正整数.
其数学模型为
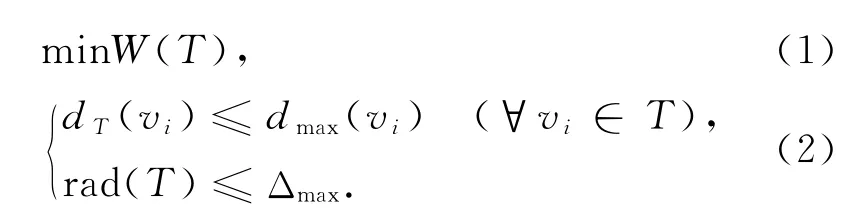
DCRCMST问题与诸多MST变形问题一样,为NP-完全问题,则该问题无有效的算法,只能用启发式算法或人工智能算法求解.下面将对DCRCMST问题的计算复杂性进行讨论.
2 DCRCMST问题的计算复杂性证明
在研究一组合优化问题的复杂性时,通常的处理方法是研究其对应的判定问题.因此,将对DCRCMST问题对应的判定形式(记为DCRCMST(D)[9])进行研究.根据文献[9]中的理论,要证明DCRCMST(D)为NP-完全问题,只需证明:①DCRCMST(D)∈NP;②一个NP-完全问题能多项式变换为DCRCMST(D).
定义3 DCRCMST(D)问题:给定无向网络G=(vs,V,E,D,W),是否存在一棵以vs为根的生成树T,使得T的总代价W(T)≤α1、半径rad(T)≤α2以及每个节点的当前度dT(vi)≤dmax(vi),其中,α1,α2∈Z+.
定义4 DCMST(D)问题:给定无向网络G=(V,E,D,W),是否存在一棵生成树T,使得T的总代价W(T)≤β1以及每个节点的当前度dT(vi)≤dmax(vi),其中,β1∈Z+.
定理 DCRCMST问题是NP-完全问题.
证明 选取一个已被证明为NP-完全的问题是度约束最小生成树(DCMST)问题,给出DCRCMST问题和DCMST问题的判定形式.
(1)先证DCRCMST(D)问题∈NP问题.
①对任意DCRCMST(D)问题的一个实例Ⅰ,任取实例Ⅰ中一棵以vs为根的生成树T′=(vs,S′,E′0),则T′的字符串输入长度是多项式时间内可计算的.
因此DCRCMST(D)问题∈NP问题.
(2)再证DCMST(D)问题可多项式变换到DCRCMST(D)问题.
任取DCMST(D)问题的一个实例Ⅱ,Ⅱ是一个无向网络G=(V,E,D,W),是否存在一棵生成树T,使得T的总代价W(T)≤β1以及每个节点的当前度dT(vi)≤dmax(vi).

Ⅱ有是的解,当且仅当对应的Ⅱ′有是的解,即DCMST(D)问题可通过f变换到DCRCMST(D)问题.
变换f中构造都是多项式时间内可完成的,则f为多项式时间变换,即DCMST(D)问题可多项式变换到DCRCMST(D)问题.
综上所述,DCRCMST(D)问题是NP-完全问题,即DCRCMST问题是NP-完全问题.
3 启发式算法
本文提出一个基于Prim算法的启发式算法.它从网络G=(vs,V,E,D,W)的根vs出发,不断扩展一棵子树T=(vs,S,E0),直到S包括原网络的全部节点,即|S|=|V|,便得到满足度、半径约束的生成树T.
其基本思想是:对V中的每个节点vi,赋予3个数值(称为标号):剩余度标号re_d(vi),记录该节点此时的剩余度,即还可接纳的最大边数;距离标号u(vi),记录在最终生成树中vs到该节点可能的长度上界;前趋标号pred(vi),记录从vs到该节点的路长取到上界u(vi),该路中节点vi前面的那个直接前趋节点.从vs出发,每次选择割[S]中满足约束的权值最小的边,然后修改节点的标号,直到|S|=|V|.算法结束时,距离标号u(vi)表示生成树T中从vs到该节点的路长,生成树T的半径
算法的具体步骤如下:
Step 0 初始化,S={vs},令剩余度标号re_d(vs)=dmax(vs),距离标号u(vs)=0,pred(vs)=0,¯S=V-S;对¯S中的节点,令剩余度标号re_d(vi)=dmax(vi),距离标号u(vi)=+∞,pred(vi)=0;当前生成树T=(vs,S,E0),E0=Ø;
Step 1 若S=V,则根据节点的前趋标号输出生成树T,结束,否则转到Step 2;
Step 2 若割[S,¯S]=Ø,则G不连通,结束,否则转到Step 3;
Step 3 将割[S,¯S]中端点和权值都满足约束的边e加入到集合S′,即对于S′中任意的边e=(v1,v2)(v1∈S,v2∈¯S),都有re_d(v1)>0,re_d(v1)-1>0,u(v1)+w(v1,v2)≤Δmax(Δmax为半径约束值).若S′=Ø,则查找失败,结束,否则转到Step 4;
Step 4 选择S′中权值最小边e*=(v′1,v′2)加入到当前生成树T,即S=S∪v′2,E0=E0∪e*;更新节点v′1和v′2的剩余度标号re_d(v′1)=re_d(v′1)-1和re_d(v′2)=re_d(v′2)-1,节点v′2的距离标号u(v′2)=u(v′1)+w(v′1,v′2),节点v′2的前趋标号pred(v′2)=v′1;转到Step 1.
算法的时间复杂度分析:该算法主要计算量是在Step 4查找割[S,¯S]中满足约束条件的最小边,该步的计算复杂度为o(m),因为Step 4最多执行n-1步,所以该算法的时间复杂度为o(mn).
4 数值实验
为了测试算法的效果,用MATLAB编程测试了大量的数据实例,均获得了良好的效果,这里只列举部分结果.
例1 如图1所示,节点规模n=5,节点的度约束在节点标号括号内给出,边上数字为边的权值,半径约束为5,设节点v1为根.
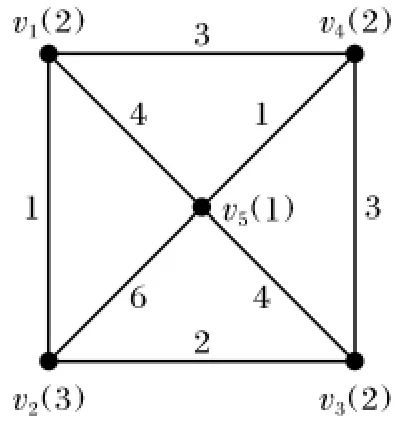
图1 例1中网络示意图Fig.1 Network schematic of example 1
用本算法求得度、半径约束最小生成树T如图2所示,总代价W(T)=7,半径rad(T)=4.

图2 例1中度、半径约束的最小生成树Fig.2 Degree-constrained,radius-constrainedminimum spanning tree in example 1
例2 选用研究度约束最小生成树常用的数据实例[3,10],节点规模n=8,度限制dmax=(dv1, dv2,…,dv8)={3,3,3,3,3,3,3,3}.设半径约束为50,节点v1为根.边的权矩阵为
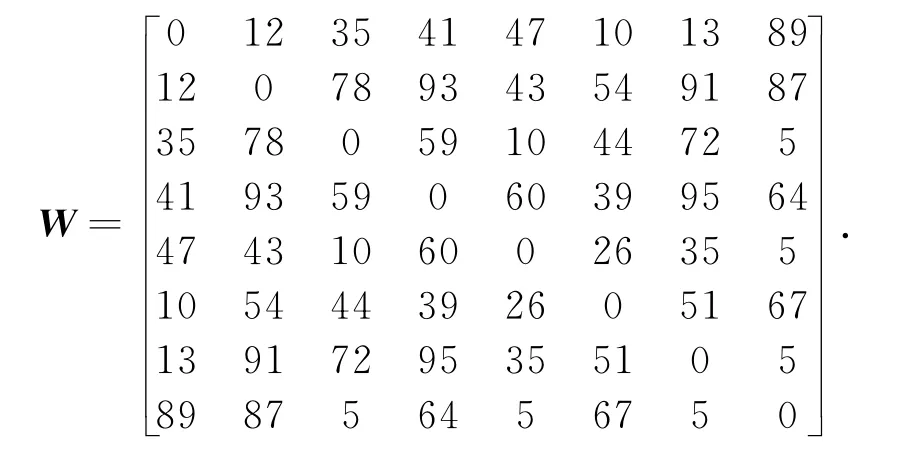
用本算法求得度、半径约束最小生成树T,总代价W(T)=125,半径rad(T)=49.
例3 为对大规模数据实例进行测试,现随机生成一个n个节点的无向网络Kn,网络中边的权值为[1,14]之间的随机整数,节点的度约束为[1,[n/2]]之间的一个随机整数.分别取节点数n=10,50,100,150,200,半径约束分别为20,40,60,80,100.设节点v1为根.
用本算法分别求得度、半径约束最小生成树T的总代价和半径如图3所示.
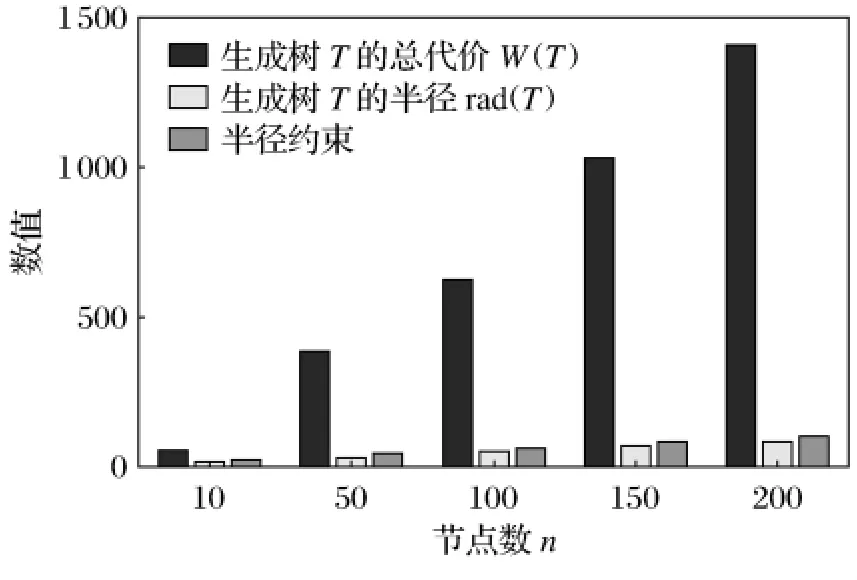
图3 例3中度、半径约束的最小生成树的总代价和半径Fig.3 Total costs and radius of degree-constrained,radius-constrained minimum spanning tree in example 3
5 结 语
DCMST问题属于异常困难的组合优化问题,DCRCMST问题是比DCMST问题复杂性更高的问题,求解的困难程度与度约束、半径约束以及图的连接性态有关.本文给出的启发式算法能在一定程度上较好地求解此问题.其他更好的求解算法有待进一步研究.
[1]Ahuja R K,Magnanti T L,Orlin J B.Network Flows:Theory,Algorithms,and Applications[M].Beijing:Mechanical Industry Press,2005.
[2]李世娟,马骥,白鹭.基于改进ID3算法的决策树构建[J].沈阳大学学报,2009,21(6):23-25.
[3]Narula S C,Ho C A.Degree-constrained minimum spanning tree[J].Computers and Operations Research,1980,7(4):239-249.
[4]Fernandez F R,Hinojosa M A,Puerto J.Multi-criteria minimum cost spanning tree games[J].European Journal of Operational Research,2004,158(2):399-408.
[5]Pendarakis D,Shi S,Verma D,et al.ALMI:An Application Level Multicast Inf rast ructure[C]∥Proceedings of the 3rd USENIX Symposium on Internet Technologies &Systems.San Francisco,2001:49-60.
[6]Chu Y H,Rao S G,Zhang H.A Case for End System Multicast[C]∥Proceedings of the ACM SIGMETRICS. Santa Clara,2002:1-12.
[7]吴家皋,叶晓国,姜爱全.一种异构环境下覆盖多播网络路由算法[J].软件学报,2005,16(6):1112-1120.
[8]Banerjee S,Bhattacharjee B.A Comparative Study of Application Layer Multicast Protocols[C]∥Submitted for Review.Francis,2002:17-25.
[9]Papadimitriou C H.Computational Complexity[M].Boston:Addison Wesley,2004.
[10]Narula S C,Ho C A.Degree-constrained minimum spanning tree[J].Computers and Operations Research,1980,7(4):239-249.
Degree-Constrained,Radius-Constrained Minimum Spanning Tree Problem and its Algorithm
SHI Lei,FENG Zuzhen,YANG Jianqiang,LONG Yao
(Department of Mathematics,Honghe University,Mengzi 661100,China)
The degree-constrained,radius-constrained minimum spanning tree problem was put forward,and it was proved to be NP-complete.A mathematics programming model of the problem and a fast heuristic algorithm were proposed to solve the model.The time complexity of the algorithm was analyzed.The algorithm was proved to be effective by analysis and experiments.
minimum spanning tree problem;heuristic algorithm;degree-constrained;radius-constrained
TP 393.4
A
1008-9225(2012)04-0063-04
2012-02-03
云南省自然科学基金资助项目(2008CD186).
石 磊(1984-),男,湖南衡阳人,红河学院助教,硕士.
李 艳】
