氢化可的松的热力学函数和晶体结构——密度泛函理论分析

曾玉香，王 超，王炳强

（1.天津渤海职业技术学院 环境工程系，天津300402； 2.天津市环境保护科学研究院，天津300191）

氢化可的松的热力学函数和晶体结构
——密度泛函理论分析

曾玉香1＊，王 超2，王炳强1

（1.天津渤海职业技术学院 环境工程系，天津300402； 2.天津市环境保护科学研究院，天津300191）

采用密度泛函理论B3LYP/6－31G和B3LYP/6－311G＊方法优化了气相状态氢化可的松的几何结构，利用优化的结构得到了氢化可的松各原子净电荷及前沿轨道分布；基于简谐振动分析求得氢化可的松的红外光谱频率和热力学函数；并计算了环己烷、乙酸丁酯、二氯乙烷、异丙醇、甲醇、水六种不同极性的溶剂对氢化可的松几何构型、电荷分布及能量的影响.结果表明，由理论计算得到的氢化可的松的晶体结构与实测的晶体结构接近.

氢化可的松；热力学函数；晶体结构；密度泛函理论；分析

氢化可的松（11β，17β，21－三羟基孕甾－4－烯－3，20－二酮）是一种重要的皮质激素类药物，能影响糖代谢，具有抗炎、抗病毒、抗休克和抗过敏等作用[1－3].研究表明，11β－OH和17β－OH是糖皮质激素特有基团，对于药物活性至关重要.陈建新对氢化可的松的结晶过程进行研究得到了氢化可的松的分子构象和热性质，并测定了在不同溶剂、不同温度下氢化可的松的溶解度[4].汤志刚等通过测定氢化可的松在有机溶剂/水体系中的分配系数研究了有机溶剂与溶质的相互作用[5].作者利用密度泛函理论[6－7]对氢化可的松的分子结构和热力学性质进行理论研究，鉴于氢化可的松在不同溶剂中的溶解度的差异，研究了氢化可的松在不同极性溶剂[8]中的结构和电荷分布的变化.

1 计算方法

用Hyperchem程序搭建氢化可的松初始模型，以AM1方法优化构型为初始值.运用Gaussian98[9]程序包，采用密度泛函B3LYP/6－31G和B3LYP/6－311G＊方法在气相中对氢化可的松的几何结构全优化.具体计算结构和原子编号如图1所示.根据参考文献[4]中的晶体结构数据，并将理论计算结果与实测的晶体结构比较分析.在B3LYP/6－31G水平下进行振动分析无虚频，表明优化构型处于势能面上的极小点，为能量最低构型.振动分析得到氢化可的松的红外光谱和热力学函数，并与实验值进行比较.选用自洽反应场（SCRF）理论中的Onsager溶剂模型，在B3LYP/6－31G水平下计算了环己烷（ε＝2.02）、乙酸丁酯（ε＝6.0）、二氯乙烷（ε＝10.36）、异丙醇（ε＝19.9）、甲醇（ε＝32.63）、水（ε＝78.39）六种不同极性的溶剂对氢化可的松几何构型、电荷分布和能量的影响.

图1 氢化可的松的几何结构图Fig.1 Geometric structure of hydrocortisone

2 结果与讨论

2.1 几何构型分析

由图1中氢化可的松的几何结构可知，主要原子处于纸平面内，O（26）－H（56）在面外.表1列出了由6－311G＊和与6－31G基组计算所得的部分键的键长、键角、二面角.6－311G＊与6－31G相比，在所有的59个化学键中有53个键键长减小，其中C（11）－O（26）变化最大，减小0.003 63nm，变化率为2.46%.仅有C（8）－C（9），C（9）－C（10），C（10）－H（35），C（16）－C（19），C（19）－C（20），C（20）－H（43）键长增大，其中C（16）－C（19）变化最大，增加0.001 07nm，变化率为0.71%.由于基组6－311G＊较6－31G增加了每个原子基函数的数量，并且在重原子上增加极化函数，所以绝大多数化学键的键长减小.但总体而言，6－311G＊和6－31G计算的键长变化不大.6－311G＊与6－31G相比，键角变化不大，变化最大的为A（11，26，56）（相差－1.545°）和A（4，11，26）（相差1.189°），但从变化率而言，差值在总键角中所占比例很少，故基本可视为两种基组对键角的计算结果没有影响.从计算结果看，三个六元环键角除A（2，10，9）外均小于120°，由于环一中存在一个双键，故环中有五个原子基本在同一个平面，环二与环三则呈现船式结构.在五元环中键角约为103°，小于平面五元环的键角108°，除与取代基相连的C（16）外其他四个碳在同一平面，四个环在空间呈现弧状结构.

根据参考文献[4]，氢化可的松分别在异丙醇和甲醇溶剂中结晶所得到的键长数据也列于表1中.由于计算结果为理想的气态环境，而在溶剂中所得晶体结构中存在氢化可的松与溶剂分子间的氢键力作用，使得C（15）－C（17）、C（16）－C（17）、C（16）－C（19）、O（22）－H（45）4个键的键长的计算值小于实测值，其他55个键的计算值大于实测值.考虑空间位阻的影响，O（22）－H（45）实际参与了与溶剂形成的氢键，计算所得键长数值比实测值小0.044 39nm，相差率为45.76%.根据表中所列氢化可的松晶体的键角与计算所得结果比较，键角增大与减小的约各占一半，变化值不影响氢化可的松的空间结构.

由以上分析可知，计算与实测的氢化可的松的结构基本接近，考虑到增大基组则计算时间以几何级数增加，所以选取6－31G基组基本可满足需要.

表1 氢化可的松的部分键长、键角和二面角Table 1 Selected bond distances，bond angles and dihedral angels of hydrocortisone

2.2 电荷分布及前沿轨道分析

表2为氢化可的松的原子净电荷和总能量.由于与O原子相连，C（2）、C（9）、C（11）、C（16）、C（19）带正电荷.C（13）在6－31G基组计算时带正电荷，6－311G＊基组计算时带负电荷，其余C原子带负电荷.O（18）所带负电荷最多，与之相连的H（45）所带正电荷最多.6－311G＊与6－31G相比，电负性原子O、H所带电荷增大，O（23）电荷增加最多，电正性原子C所带电荷减少，C（25）电荷减少最多.

表2 氢化可的松的原子净电荷（e）、偶极矩和总能量Table 2 The atomic charges（e），dipole and total energies of hydrocortisone

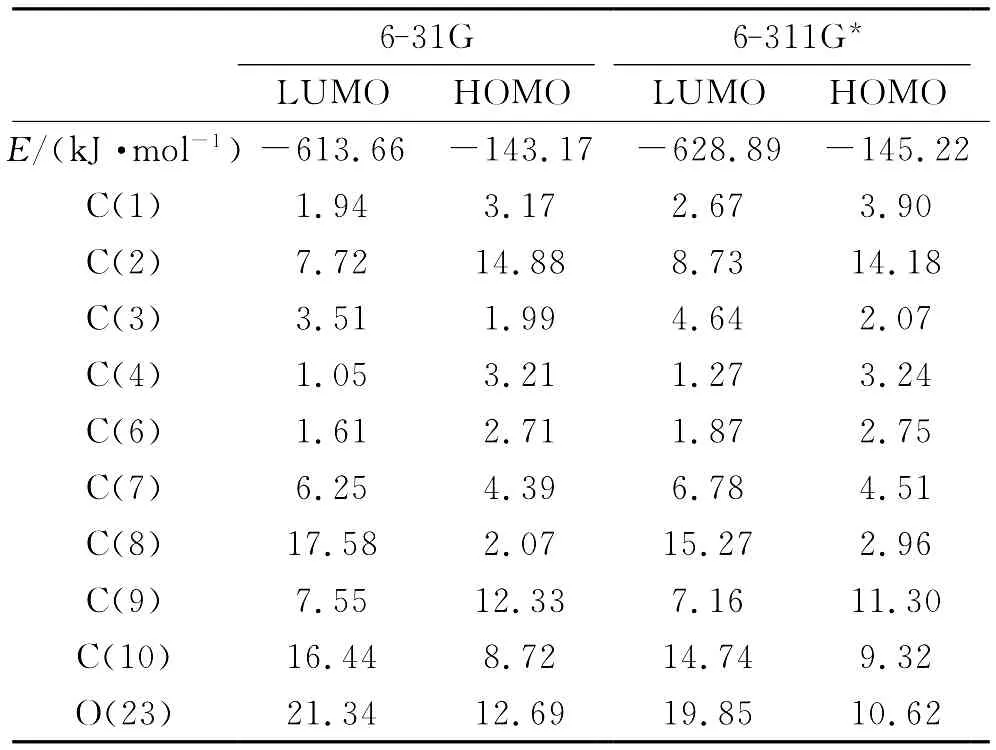
表3 前沿分子轨道能量及轨道组成（%）Table 3 Frontier molecular orbital energy and orbital compositions（%）

表3为氢化可的松的前沿分子轨道能量及轨道组成.HOMO与LUMO的能量差6－311G＊计算为483.67kJ·mol－1，6－31G计算为470.49kJ·mol－1，说明氢化可的松较稳定.6－311G＊和6－31G计算的轨道组成基本接近，图2表示6－311G＊基组计算的前沿分子轨道HOMO和LUMO分布图，表明轨道具体分布情况.HOMO轨道主要位于 C（8）、C（10）、O（23），LUMO轨道主要位于C（2）、C（9）、O（23）.

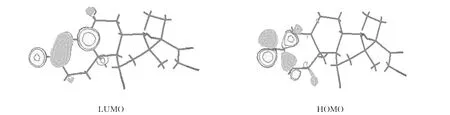
图2 B3LYP/6－311G＊计算得到的氢化可的松的LUMO和HOMO轨道分布图Fig.2 LUMO and HOMO orbit of hydrocortisone calculated by B3LYP/6－311G＊

2.3 红外振动频率与热力学参数

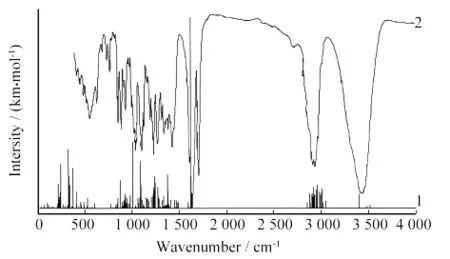
图3 理论计算和实测的氢化可的松的红外谱图Fig.3 Imitated and observed experimental FTIR spetra of hydrocortisone

基于简谐振动分析，选取校正因子0.96得到氢化可的松的162个基频振动，如图3中曲线2所示.3 516cm－1为 O（18）－H（42）伸缩振动峰，3 482 cm－1为O（26）－H（56）伸缩振动峰，3 401cm－1为O（22）－H（45）伸缩振动峰，3 053cm－1为不饱和C（10）－H（35）伸缩振动峰，3 026cm－1至2 854 cm－1各峰为C－H 伸缩振动峰，1 626cm－1为C（19）O（21）伸缩振动峰，1 623cm－1为C（9）O（23）伸缩振动峰，1 597cm－1为C（2）C（10）伸缩振动峰，1 493cm－1至877cm－1各峰为C－H变形振动峰，629cm－1至222cm－1各峰为C－H摇摆振动峰.图3中曲线1表示氢化可的松的标准谱图，其中3 428 cm－1为O－H伸缩振动峰，2 940cm－1为C－H伸缩振动峰，1 715cm－1、1 645cm－1为CO伸缩振动峰，1 430cm－1、1 390cm－1、1 270cm－1、1 235cm－1为C－H变形振动峰.理论计算与实测的红外光谱图的峰强、峰位基本相同，可以用理论计算来辅助进行红外光谱图的解析.

在全优化构型和振动分析基础上，根据统计热力学公式求得氢化可的松在200～800K温度范围内的标准恒压热容、标准熵和标准焓，计算结果列于表4.随着温度的升高，标准恒压热容、标准熵和标准焓均增大，三者与温度之间的关系可用多项式拟合，相关系数达0.999 8.

表4 氢化可的松在不同温度下的热力学参数Table 4 Thermodynamic properties of hydrocortisone at different temperatures

2.4 不同溶剂对氢化可的松的影响

氢化可的松在真空以及环己烷、乙酸丁酯、二氯乙烷、异丙醇、甲醇、水六种不同极性溶剂条件下计算得到的键长、键角、二面角列于表5中.随着溶剂极性的增加，有15个键的键长增长，14个键的键长减小，30个键键长变化不大，其中C（13）－C（16）键长减小最多，缩短0.004 5nm，C（14）－C（15）键长增加最多，增长0.003 7nm.键长的最大变化率仅为0.28%.随着溶剂极性的增加，有42个键角增大，39个键角键小，19个键角先减小后增大，如C（4）－C（5）－C（14），17个键角先增大后减小，如C（6）－C（5）－C（14）.其中键角C（5）－C（4）－C（11）增大最多为0.672 1°，键角C（13）－C（16）－O（18）减小最多为0.632°，最大变化率为0.61%.随着溶剂极性的增加，73个二面角增大，127个二面角键小.二面角C（16）－C（13）－C（14）－H（37）增加最多为5.847 9°，C（17）－C（16）－O（18）－H（42）减小最多为0.683 03°.由于二面角的数值范围从2.6°～179.8°，C（7）－C（1）－C（4）－C（11）变化率最多为302%.从以上分析可知，溶剂的极性变化对分子键长和键角的影响不大，对二面角稍有影响.

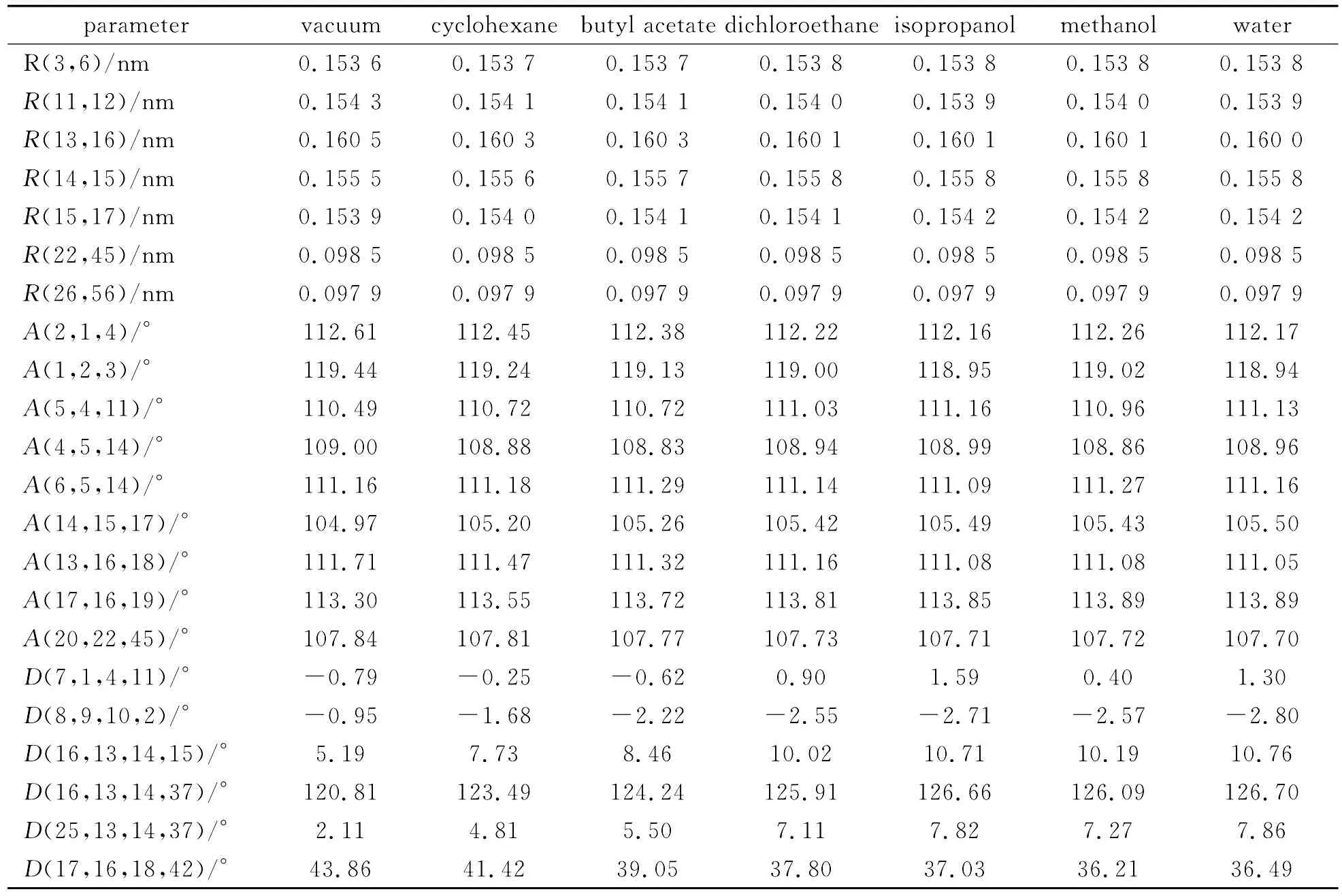
表5 不同溶剂条件下部分键长、键角和二面角Table 5 Bond distances，bond angles and dihedral angels of hydrocortisone in different solvents

表6为不同溶剂条件下氢化可的松的原子净电荷和前沿分子轨道能量.

从表6可以看出，随着溶剂极性的增加，电荷的变化没有比较明显的规律.其中H（36）电荷增加最多，电荷增加0.012 9，C（13）电荷增加率最大，增加24.21%.C（12）电荷减少最多，减少0.012 2，H（33）电荷减少率最大，减少5.87%.随着溶剂极性的增加，分子偶极矩增大，表明在强极性溶剂中氢化可的松极性增大.前线分子轨道能量差增大，说明在极性较强的溶液中氢化可的松更趋于稳定.根据参考文献[4]，在环己烷、乙酸丁酯、1，1－二氯乙烷、异丙醇中氢化可的松的溶解度分别为0.002g/L、2.12g/L、2.64g/L、6.08g/L，与计算结果中氢化可的松在溶剂中性质变化规律非常符合.因为影响溶解度的因素较多，参考以上计算结果可以将溶剂极性作为衡量溶解度的指标之一，能较好地模拟各种因素对溶解度的影响[10].结论：1）运用B3LYP/6－31G和B3LYP/6－311G＊在气相中计算所得的氢化可的松的结果与实测结果基本接近，选用B3LYP/6－31G研究氢化可的松与溶剂的相互作用已能够满足需要.2）在环己烷、乙酸丁酯、二氯乙烷、异丙醇、甲醇、水六种溶剂中，氢化可的松结构变化不大，随着溶剂极性的增加，分子偶极矩增大，前线分子轨道能量差增大，氢化可的松在溶剂中的溶解度增大.

表6 不同溶剂条件下氢化可的松的原子净电荷（e）、偶极矩和能量Table 6 The atomic charges（e），dipole，energies of hydrocortisone in different solvents

续表6

[1]United States Pharmacopeial Convention.Hydrocortisone：United States pharmacopeia[M].24.Rockille：United States Pharmacopeial Convention，Inc.2000：823－824.

[2]FLORIO S，CIARCIA R，CRISPINO L.HC has a protective effect on cyclosporine A－induced cardiotoxicity[J].J Cell Phy，2003，195（1）：21－26.

[3]SAKUMA E，SOJI T，HERBERT D C.Effects of hydrocortisone on the formation of gap junctions and the abnormal growth of cilia within the rat anterior pituitary gland：possible role of gap junctions on the regulation of cell development[J].Anatomical Record，2001，262（2）：169－175.

[4]陈建新.氢化可的松结晶过程研究[D].天津大学，2005.

[5]汤志刚，胡熙恩，朱 永.溶剂萃取法分离氢化可的松和表氢化可的松[J].化学工程，1998，26（5）：51－55.

[6]KOHN W，BECKE A D，PARR R G.Density functional theory of electronic structure[J].J Phys Chem，1996，100（31）：12974－12980.

[7]LEE C，YANG W T，PARR R G.Development of the colle－salvetti correlation－energy formula into a functional of the electron density[J].Phys Rev B，1988，37（2）：785－789.

[8]李会学，王晓峰，董小宁，等.烟酸二聚体的结构与性质[J].物理化学学报，2009，25（1）：161－168.

[9]FRISCH M J，TRUCKS G W，SCHLEGEL H B，et al.Gaussian 98，Revision A9[CP].Gaussian，Inc.Pittsburgh P A，1998.

[10]曾玉香，王 超，王炳强.应用人工神经网络预测氢化可的松的溶解度[J].应用化学，2009，26（11）：1367－1370.

Thermodynamic function and crystal structure of hydrocortisone——Analysis by density functional theory

ZENG Yu－xiang1＊，WANG Chao2，WANG Bing－qiang1

（1.DepartmentofEnvironmentalEngineering，TianjinBohaiVocationalTechnicalCollege，Tianjin300402，China；2.TianjinAcademyofEnvironmentalSciences，Tianjin300191，China）

The geometric structure of hydrocortisone was calculated and optimized at the B3LYP/6－31Gand B3LYP/6－311G＊level of density functional theory.The atomic charges and frontier molecular orbitals of hydrocortisone were obtained based on the optimized structure；and its infrared spectrum vibrational frequencies and thermodynamic properties were calculated using simple harmonic vibration method.Moreover，the effects of six kinds of solvents with different polarity，including cyclohexane，butyl acetate，1，1－dichloroethane，iso－propanol，methanol，and water，on the geometric structure，atomic charges and energy of hydrocortisone were calculated.Results indicate that the calculated crystal structure of hydrocortisone agrees well with the experimental one.

hydrocortisone；thermodynamic function；crystal structure；density functional theory；analysis

O 641

A

1008－1011（2012）01－0047－06

2011－07－09.

天津市高等学校科技发展基金计划项目（编号20060218）.

曾玉香（1981－），女，讲师，研究方向为工业分析与检验，＊

，E－mail：cengyx99＠126.com.