自相似测度对一些参数的连续依赖性

丁道新

(湖北第二师范学院数学与数量经济学院，湖北 武汉 430205)

0 引言

关于分形测度或更一般的概率测度的Fourier分析以及各种性质的研究在近些年分形领域引起广泛的兴趣[1-6].本文中主要考虑自相似测度对一些参数的连续依赖性.设f1，f2，…fN，是d上的一族压缩映射，那么{fi组成一个压缩迭代函数系统(IFS)，则存在唯一的非空紧集K使得紧集K称为关于压缩迭代函数系统的不变集(或称为吸引子).若映射为相似映射，我们称这时的不变集为自相似集.通常情况下K或者K的边界是分形集.对任意概率向量P(即存在唯一Borel概率测度μ使得

(1)

这里μ称为自相似测度，且supp(μ)=K.关于自相似集的详细论述参见文献[7-8].

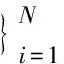
设(X，d)是紧度量空间，用M表示X上的概率测度的全体，即若μ∈M，则μ是X上的测度，并且μ(X)=1.用C(X)表示X→的连续函数的全体.称f∈C(X)是Lipschitz函数，如果存在常数Mf，使得

|f(x)-f(y)|≤Mfd(x，y)，∀x，y∈X，

这里Mf称为f的Lipschitz常数，一般它随f而变.特别地，若Mf=1，则记f∈Lip1.

定义1M上的Hutchinson度量dH定义为

我们可以得到：(1)dH是M上的度量；(2)(MdH)是完备度量空间[10].

我们再回到迭代函数系统，设{Kn}n∈是d上相似压缩迭代函数系统列{{fin(x)=sinOx+ain}n∈所生成的自相似集列，K是相似压缩迭代函数系统{fi(x)=siOx+ai所生成的自相似集，其中O是正交矩阵，ain，ai∈d(i=1，2，…，N).记Sn=(s1n，s2n，…，sNn)和S=(s1，s2，…，sN)，S的范数取‖S‖∞=max{si:1≤i≤N}，则当Sn、ain分别依范数收敛于S、ai时，Kn将依Hausdorff度量收敛于K[9].因此，存在一个紧集E⊂d使得K⊂E且Kn⊂E，∀n∈.设μn是支撑在Kn上相对概率向量Pn=(p1n，p2n，…，pNn)的自相似测度，μ是支撑在K上相对概率向量P=(p1，p2，…，pN)的自相似测度.取X∶=E，我们有下面的结果.

定理1如果Sn→S，Pn→P，ain→ai(n→∞)，i=1，2，…，N则dH(μn，μ)→0.

1 定理1的证明

(2)

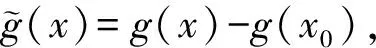
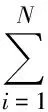
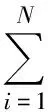
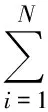
由g的任意性我们得到(2)式.

对任意g∈Lip1，由(1)式我们得

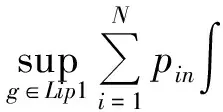
因为suppμ=K是一个紧集，所以存在一个正常数C使得对任意x∈K有‖x‖≤C，于是

.

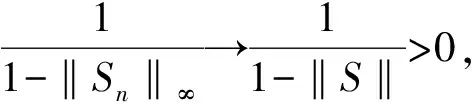
我们知道自相似测度对Lebesgue测度要么是奇异的要么是绝对连续的[11]，比如作为一种自相似测度的Bernoulli卷积：

由定理1知当n→∞时有dH(μρ，n，μρ)→0，然而我们有下面的结果.

命题1存在一个Borel集B⊂使得序列不收敛于μ1/2(B).

Ti(x)=ρ(x+bi)，0<ρ<1，ρ-1∈，bi∈，1≤i≤N

(3)

其中bl=0.我们有下面的引理[14].

p1+p2Zb2+…+pNZbN=0

(4)

则相应的自相似测度μ是奇异的.

上面的结果也被Hu[15]和Niu[16]使用不同的技巧获得.保持引理1的假设条件，得到下面的结果.

推论1如果存在某个i∈{1，2，…，N}使得pi>1/2，则μ是奇异的.

p1=|p2Z0b2+…+pNZ0bN|≤p2+…+pN=1-p1,

得到p1≤1/2，显然矛盾！这样就证明了方程(4)没有单位根.再由引理1知μ是奇异的.

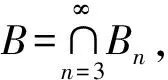
[1] Dutkay D E，Han D G，Sun Q Y. On the spectra of a Cantor measure[J].Adv Math，2009，221(1):251-276.

[2] Hu T Y，Lau K S. Spectral property of the Bernoulli convolutions[J].Adv Math，2008，219(2):554-567.

[3] Jorgensen Palle E T，Kornelson Keri A，Shuman Karen L. Affine systems: asymptotics at infinity for fractal measures[J].Acta Appl Math，2007，98(3):181-222.

[4] Li J L. On the μm,D-orthogonal exponentials[J].Nonlinear Analysis，2010，73:940-951.

[5] Laba I，Wang Y. Some properties of spectral measures[J].Appl Comput Harmon Anal，2006，20(1):149-157.

[6] Strichartz R. Convergence of mock Fourier series[J].J Anal Math，2006，99:333-353.

[7] Hutchinson J E. Fractal and self similarity[J].Indian Univ Math J，1981，30:713-747.

[8] 文志英.分形几何的数学基础[M].上海: 上海科学技术教育出版社，1999.

[9] 丁道新，朱志勇.自相似集的收敛与构造[J].喀什师范学院学报，2007，28:24-25.

[10] 沙震，阮火军.分形与拟合[M].杭州: 浙江大学出版社，2005.

[11] Peres Y，Schlag W，Solomyak B.Sixty years of Bernoulli convolutions[M].Fractal geometry and stochastics，11，vol，46，Basel: Birkhauser；2000(Greifswald/Koserow，1998)，39-65.

[12] Erdos P. On family of symmetric Bernoulli convolutions[J].Amer J Math，1939，62:974-976.

[13] Garsia A M. Arithmetic properties of Bernoulli convolution[J].Trans Amer Math Soc，1962，102:409-432.

[14] Li J L. Singularity of certain self-affine measures[J].J Math Anal Appl，2008，347:375-380.

[15] Hu T Y. Asymptotic behavior of Fourier transforms of self-similar measures[J].Proc Amer Math Soc，2000，129:1713-1720.

[16] Niu M，Xi L F. Singularity of a class of self-similar measures[J].Chaos Solitons & Fractals，2007，34:376-382.