硼铝硅系透明玻璃陶瓷晶相生长的分形动力学
2012-01-04侯朝霞
侯朝霞
(沈阳大学 辽宁省先进材料制备技术重点实验室,辽宁 沈阳 110044)
硼铝硅系透明玻璃陶瓷晶相生长的分形动力学
侯朝霞
(沈阳大学 辽宁省先进材料制备技术重点实验室,辽宁 沈阳 110044)
通过熔融法结合两步热处理制度制备了硼铝硅系透明玻璃陶瓷.基于R.Kopelman等人对分形结构中扩散控制反应速率的研究结果,探讨了硼铝硅系透明玻璃陶瓷中晶相生长的分形动力学.结果表明,用分形结构扩散控制反应动力学理论来分析硼铝硅系透明玻璃陶瓷的晶化过程是行之有效的,通过实验数据拟合得出分形子谱维数dS=1.269.
玻璃陶瓷;晶相生长;动力学;分形
在凝聚态结构中,存在着两大类实空间有规律的结构:平移不变性的周期结构和标度不变性的分形结构.对于前者,人们已进行了相当深入的研究,所形成的概念、理论和研究方法在化学领域得到了广泛应用.对于后者,则由分形几何理论的创建,而开拓出一个崭新的研究领域[1].在陶瓷材料的显微结构中,不同的显微组元或不同部位的同一类组元,其几何形状往往呈现不同的不规则程度,即具有不同的分形维数值,这与陶瓷反应动力学生长过程有关.陶瓷晶相生长过程的本质,一般认为主要是曲率半径的驱动力以及原子随机行走与时间关系的变化过程[2].近年来,从理论和实验研究中发现,由于分形介质中的扩散过程具有一些反常的行为,导致分形介质中的扩散控制反应具有一些新的特性.
1982年,Alexander和Orbach提出的分形子理论[3],对分形结构反应和扩散问题的研究起到了巨大的推动作用.利用分形几何模型代替欧氏几何模型研究分子的吸附、扩散和反应动力学过程,进而对非线性化学动力学有了更深刻的认识.R.Kopelman[4]对分形结构中扩散控制反应速率进行了较为深入的研究,本文基于R.Kopelman的研究结果,对硼铝硅系透明玻璃陶瓷中晶相生长进行了分形动力学研究.目前,有关硼铝硅系透明玻璃陶瓷晶相生长分形动力学方面的研究国内外尚未见相关报道.
1 实 验
原料组成(质量分数,%):37SiO2-20Al2O3-28B2O3-8ZnO-3(Li2O+K2O)-1Sb2O3-3(TiO2+Zr O2).配合料经球磨机充分混合后倒入刚玉坩埚中,采用硅钼电阻炉,在1 400℃熔融2 h,玻璃液经澄清均化后注入预热不锈钢模具,熔体迅速降温固化成型.将玻璃体置于550℃马弗炉内退火2 h,然后随炉降至室温.将退火后的样品切割成10 mm×10 mm×5 mm的小块,样品于700℃成核2 h,760℃分别晶化热处理1、2、3、4和5 h.将热处理后的样品研磨抛光成10 mm×10 mm×1 mm的薄片,并经5%氢氟酸腐蚀5 s.
采用日本日立S-4200型扫描电镜测定玻璃陶瓷中晶粒尺寸、形貌及在残余玻璃相中的分布.采用SISC IASV 8.0图像分析仪,在各样品的扫描电镜照片上随机选取10个视场,测定晶相的面积百分数.
2 R.Kopelman的反应模型
从本质上分析,影响化学反应速率的因素有两个:化学内禀反应速率和分子的扩散速率.当分子扩散速率比内禀反应速率小很多时,扩散就成为控制反应过程的主要因素,通常称为扩散控制反应[5].
对于分形介质中扩散控制的双分子反应,R.Kopelman采用如下准单分子反应模型进行简化处理:反应分子a和b随机地分布在点阵格位上,分子a看成是固定在某些格位上,起着“陷阱”的作用;分子b在点阵上的扩散运动作为随机行走过程,当 分子b随机行走到 分子a所占的格位时,立即发生反应.当t=0时,分子b的质量浓度ρ=ρ0,在t时刻,分子b与分子a发生反应的概率用p(t)表示,由于[1-p(t)]是t时刻分子 b还存活的概率,因此可把t时刻分子b的质量浓度ρ(t)表示为

由式(1)可知,ρ(t)应满足如下反应速率方程:
dlnρ(t)/dt=- [1-p(t)]-1[dp(t)/dt],(2)
也可以把式(2)写为如下形式:

显然,式(4)反映了准单分子反应模型中反应速率系数k(t)与反应概率p(t)之间的关系.
用S(t)表示随机行走的分子b在点阵中行走了t时间后所访问过的不同格位的数目,Kopelman R等人得到了p(t)与S(t)之间的关系.用N表示点阵中格位的总数目,在N个格位上分布S(t)个 分子b的方式的数目为
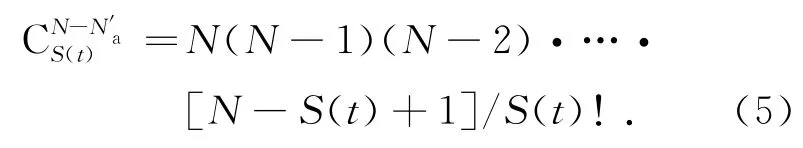
用N′a表示t时刻在点阵中已被分子a占据的格位的数目,在 (N-N′a)个格位上分布S(t)个b分子的方式的数目为

由式(5)和式(6),得
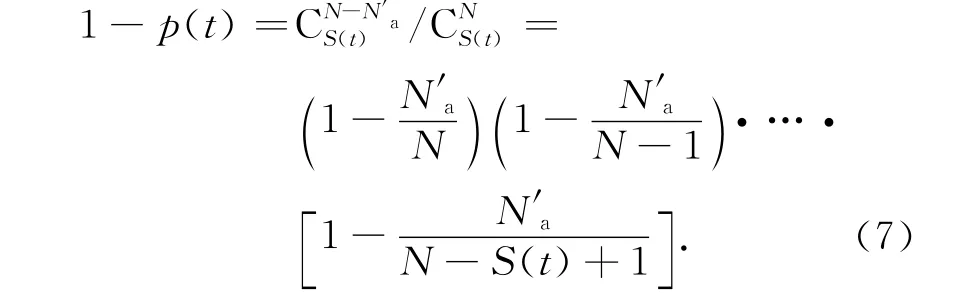
若S(t)≪N,则式(7)简化为
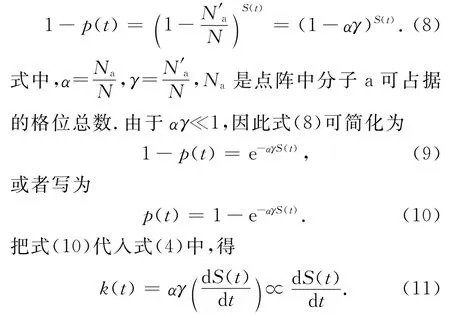
式(11)反映了随机行走过程的参量S(t)与反应速率过程的宏观量k(t)间的内在联系,它是从理论上研究分形介质中反应速率系数的一个重要关系式.
在欧氏空间中,S(t)∝t.由式(11)可得到k=k0=常数,也就是说,扩散控制反应速率系数是与时间无关的常数.这与M.V.Smoluchowski理论所得到的结果一致.但是对于分形介质而言,S(t)遵从式(12)所表达的规律:S(t)∝t ds/2. (12)
式中,ds为分形子谱维数(简称分维数),它是描述分形结构中动力学行为的重要参量.
把式(12)代入式(11)中,可得到分形介质中扩散控制的反应速率系数为

也可把式(13)写为

式中,k0是与时间无关的常数.在分形介质中,由于ds<2,因此总有h>0.
式(15)表明:在分形介质中,扩散控制反应速率系数不再是与时间无关的常数,而表现出随时间而变化的反常行为,且随时间变化的指数h的数值与分维数ds有关.
3 结果与讨论
图1给出了760℃分别晶化热处理1、2、3、4和5 h后获得的透明玻璃陶瓷样品的扫描电镜照片.采用SISC IASV 8.0图像分析仪,在上述5张扫描电镜照片上分别随机选取10个视场,测定晶相所占的面积百分数,可将晶相视为固定在格位上的a组元,玻璃相中的扩散组元视为b,则运用R.Kopelman所采用的反应模型来分析晶相生长的分形动力学.测得的晶相面积百分数取平均值列于表1中,晶相面积百分数的平均值反映出晶化体积分数,为方便起见,这里用单位时间晶化的体积百分数表示晶化速率.晶化体积百分数与晶化时间的关系如图2所示.为便于说明,将图2中的曲线图进行了适当的外延.
由图2,可将晶化过程分为3个阶段:第一阶段约在热处理1 h以内,晶化过程受化学反应控制,晶化速率是一定值;第二阶段是在热处理1~3 h之间,晶化过程受化学反应和扩散共同控制;第三阶段是在热处理3 h以后,扩散成为晶化过程的主要控制因素,曲线斜率逐渐降低,晶化速率逐渐下降.

表1 不同晶化热处理时间样品的平均面积百分数Table 1 Percentage of the average area of different crystallization heat treatment time samples

图1 硼铝硅系透明玻璃陶瓷扫描电镜照片Fig.1 SEM photographs of boron aluminosilicate transparent glass-ceramics
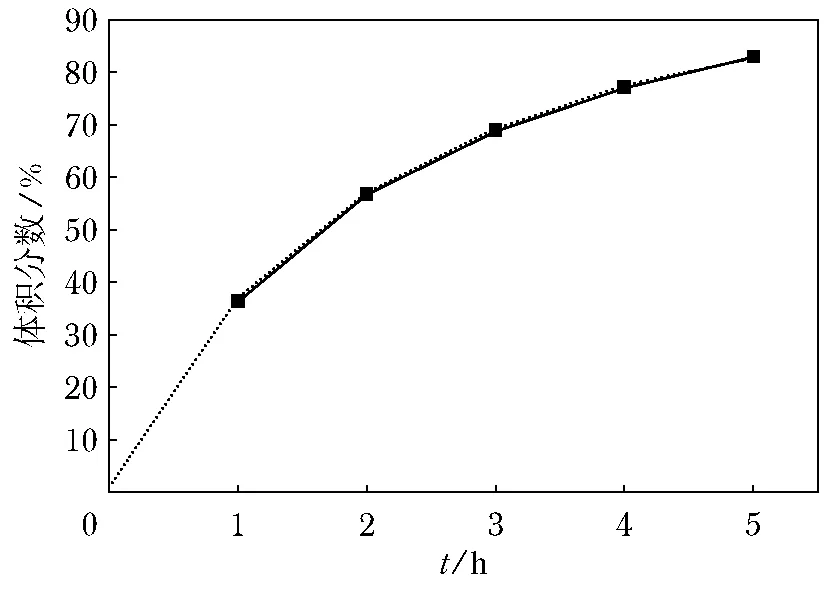
图2 晶相体积分数与热处理时间的关系曲线Fig.2 Relationship of the crystal phase volume percent and the heat-treatment duration
将第一段和第二段晶化过程分别绘成曲线示于图3和图4中.图3和图4中的曲线采用origin软件经方程拟合可以计算出第一和第二阶段晶相生长速率与时间的关系式,UⅠ=34.55 nm/h(0<t<1h);UⅡ= 46.18t-0.3656(3h<t<5h),即k(t)=46.18t-0.3656.根据分形理论得出式(14)中h=0.365 6,dS=1.269.
图3 反应控制晶化阶段Fig.3 Reaction control section during crystallization

图4 扩散控制晶化阶段Fig.4 Diffusion control section during crystallization
4 结 论
用分形子谱维数来分析分形结构扩散控制化学反应,能够揭示其与经典化学反应动力学的不同及反应动力学与分形结构的联系.经实验数据拟合计算得出分维数dS=1.269.运用分形结构扩散控制反应动力学理论来分析硼铝硅系透明玻璃陶瓷的晶化过程是行之有效的.
[1] 王甲春,唐明.分形结构双分子基元反应扩散动力学理论分析[J].沈阳建筑工程学院学报,2001,17(3):210-213.
[2] Rahaman M N.Ceramic Processing and Sintering[M].New York:Marcel Dekker Inc.,1995:15-16.
[3] Kingery W D,Bowen H K,Uhlmann D R.陶瓷导论[M].清华大学无机非金属材料教研组,译.北京:中国建筑工业出版社,1987:330.
[4] Kopelman R.Fractal Reaction Kinetics[J].Science,1988,241(4873):1620-1626.
[5] 梁英教.物理化学[M].北京:冶金工业出版社,1995:282.
On Fractal Kinetics of Crystal Growth in Transparent Boron Aluminosilicate Glass-Ceramics
HOUZhaoxia
(Liaoning Provincial Key Laboratory of Advanced Materials,Shenyang University,Shenyang 110044,China)
Boron aluminosilicate transparent glass-ceramics were prepared by melting method and twostep heat-treatment process.Fractal kinetics of crystal growth in transparent boron aluminosilicate glass-ceramics was analyzed based on the research results of Kopelman R et al.concerning the diffusion control reaction velocity in fractal structure.It turned out that it is feasible to analyze the crystallization process of boron aluminosilicate transparent glass-ceramics by diffusion control reaction kinetics theory in fractal structure.The fractal dimensiondS=1.269 is fitted by experimental data.
glass-ceramics;crystal growth;kinetics;fractal
TQ 174.1
A
1008-9225(2012)02-0045-04
2011-12-05
侯朝霞(1971-),女,山东高密人,沈阳大学副教授,博士.
刘乃义】
