序半群中有边界值的直觉模糊理想

黄晓昆，程 涛

（1.红河学院 数学学院，云南 蒙自 661100；

2.廊坊燕京职业技术学院 公共教学部，河北 三河 065200）

序半群中有边界值的直觉模糊理想

黄晓昆1，程 涛2

（1.红河学院 数学学院，云南 蒙自 661100；

2.廊坊燕京职业技术学院 公共教学部，河北 三河 065200）

介绍了序半群中具有边界值（α，β）的直觉模糊理想的概念，并对其相关运算性质进行了探讨.最后，通过有边界值（α，β）的直觉模糊理想，对内正则序半群的特征进行刻画，得到若干刻画定理.

序半群；直觉模糊理想；完全格；正则序半群

继L.A.Zadeh提出模糊集（Fuzzy Sets）的概念［1］之后，A.Rosenfeld于1971年提出了模糊子群的概念［2］，这标志着一个新的数学分支—— 模糊代数—— 从此产生.在此后的30多年里，一大批学者对该领域的工作产生了浓厚的兴趣，通过他们的不懈努力，目前该领域的研究已取得了丰硕的成果［3－8］.1986年，保加利亚学者 Atanassov K T提出了直觉模糊集的概念，并指出直觉模糊集是模糊集的推广［9］.此后，许多学者将直觉模糊集理论引入代数结构的研究，例如Biswas R在文献［10］中将直觉模糊集的概念引入群论中，研究了直觉模糊子群；K.H.Kim和Y.B.Jun在文献［11］中提出了半群中直觉模糊理想的概念.W.A.Dudek和B.Davvaz等人分别对超准群中的直觉模糊子超准子群和直觉模糊Hv子模进行了研究［12－13］，A.Khan等人在文献［14］中对序半群上的直觉模糊双理想进行了详细的讨论，并利用此概念，对序半群的正则性进行了刻画.

在前人工作的基础上，本文将直觉模糊集的概念应用于序半群的研究中，引入了序半群中具有边界值（α，β）的直觉模糊理想的概念，对其性质进行了探讨，并利用有边界值（α，β）的直觉模糊理想，对内正则序半群的特征进行了刻画，得到若干刻画定理.

1 预备知识

序半群是一个由非空集合S、一个元运算“·”以及一个序关系“≤”组成的代数系统（S，·，≤），其中，（S，·）是一个半群，且满足∀x，y，a，b∈S，若x≤y，则ax≤ay，xb≤yb.序半群S的元素e称为一个单位元，如果∀x∈S，均有e＝xe＝ex.

定义1.1 序半群S的一个子集E叫做S的左（右）理想，如果满足：①SE⊆E（ES⊆E）；（②∀x∈S，若存在y∈E满足x≤y，则x∈E.序半群S的子集E叫做一个理想，如果E既是S的左理想又是S的右理想.

对序半群S的任意一子集E，记：（E］＝｛x∈S｜存在y∈E，x≤y｝.

设X是非空集合，映射μ：X→［0，1］称为X上的一个模糊集.对E⊆X和r∈［0，1］，以下用符号r E表示X上的一个模糊集：∀x∈X，若x∈E，则r E（x）＝1；若x∉E，则r E（x）＝0.显然，对∀E⊆X，1E＝χE（其中，符号χE表示E的特征函数）.

作为模糊集概念的重要推广，接下来介绍直觉模糊集.

定义1.4 设S是序半群，A，B∈IF（S）且α，β∈［0，1］满足α＜β.规定IF（X）上的序关系“⊆（α，β）”如下：

A⊆（α，β）B⇔∀x∈S，μB（x）∨α≥μA（x）∧β，γB（x）∧（1－α）≤γA（x）∨（1－β）.

性质1.1 设S是序半群且A，B，C∈IF（S），则A。（B。C）＝（A。B）。C.

性质1.2 设S是序半群且A，B，C，D∈IF（S）且α，β∈［0，1］满足α＜β，则

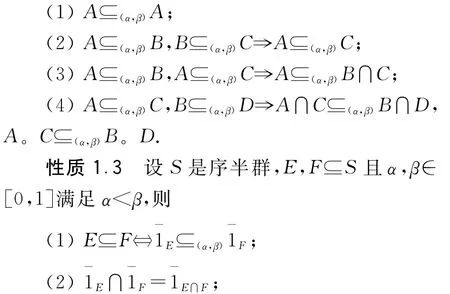
定义1.6 设S是序半群且α，β∈［0，1］满足α＜β.定义IF（S）上的二元关系“～（α，β）”如下：对任意的A，B∈IF（X），A～（α，β）B⇔A⊆（α，β）B，B⊆（α，β）A.

根据性质1.2，“～（α，β）”是IF（S）上的一个等价关系.

2 序半群中有边界值的直觉模糊理想

定义2.1 设S是序半群，A＝（μA，γA）∈IF（S）且α，β∈［0，1］满足α＜β.A称为一个有边界值（α，β）的直觉模糊左理想，如果对∀x，y∈S，有

（F1a）max｛μA（xy），α｝≥min｛μA（y），β｝且min｛γA（xy），1－α｝≤max｛γA（y），1－β｝；

（F2a）∀x，y∈S，若x≤y，则

max｛μA（x），α｝≥min｛μA（y），β｝且 min｛γA（x），1－α｝≤max｛γA（y），1－β｝.

此外，序半群上有边界值（α，β）的直觉模糊右理想和有边界值（α，β）的直觉模糊理想可类似定义.

设S是有单位元e的序半群，A是S的有边界值（α，β）的直觉模糊左理想，则对x∈S，显然有max｛μA（e），α｝≥min｛μA（x），β｝，min｛γA（e），1－α｝≤max｛γA（x），1－β｝.

作为序半群上有边界值（α，β）的直觉模糊左理想的例子，给出如下结论.

定理2.1 设S是序半群且E⊆S.E是S的左（右）理想当且仅当1－E是S的有边界值（α，β）的直觉模糊左（右）理想.

引理2.1 设S是序半群且A∈IF（S）.A是S的一个有边界值（α，β）的直觉模糊左（右）理想当且仅当下列条件成立：

max｛μA（x），α｝≥min｛μA（y），β｝且 min｛γA（x），1－α｝≤max｛γA（y），1－β｝.

证明 只需证明（1）等价于（F1a）.假设（F1a）成立，则有

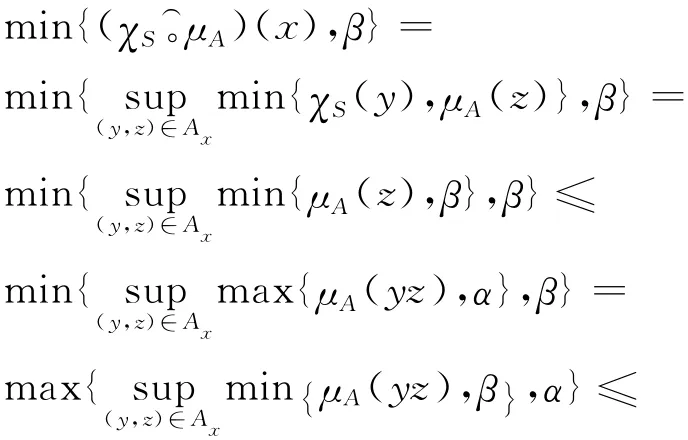
因此，条件（F1a）成立.

定理2.2 设S是序半群，A∈IF（S）且α，β∈［0，1］满足α＜β.A是S的一个有边界值（α，β）的直觉模糊左（右）理想当且仅当∀r∈［α，β），t∈（1－α，1－β］，S的非空子集A（r，t）都是S的左（右）理想.

证明略，容易直接验证.

推论 设S是序半群，A∈IF（S），α1，α2，β1，β2∈［0，1］满足α1＜α2＜β2＜β1，则S的每一个有边界值（α1，β1）的直觉模糊左（右）理想都是有边界值（α2，β2）的直觉模糊左（右）理想.

定理2.3 设S是序半群，α，β∈［0，1］满足α＜β.若A，B∈IF（S）都是S的有边界值（α，β）的直觉模糊左（右）理想，则A∩B也是S的有边界值（α，β）的直觉模糊左（右）理想.

证明略，容易直接验证.

定义2.2［5］序半群S称为内正则的，如果对∀x∈S，存在a，b∈S，使得x≤ax2b.其等价定义为：（1）∀x∈S，x∈（Sx2S］；（2）∀E⊆S，E⊆（SE2S］.

引理2.2［5］S是内正则序半群当且仅当对S的任一左理想L和任一右理想R，有L∩R⊆L。R.

定理2.4S是内正则序半群当且仅当对S的任一有边界值（α，β）的直觉模糊左理想A和任一有边界值（α，β）的直觉模糊右理想B，均有A∩B⊆（α，β）A。B.

证明 假设S是内正则序半群，A是S的一个有边界值（α，β）的直觉模糊左理想，B是一个有边界值（α，β）的直觉模糊右理想，则∀x∈S，存在a，b∈S，使得x≤ax2b＝（ax）（xb）.于是

由性质1.3得L∩R⊆L。R.因此，根据引理2.2，S是内正则序半群.

定理2.5 序半群S是内正则的当且仅当对S的任意有边界值（α，β）的直觉模糊理想A，均有A～（α，β）A＊2.

证明 设S是内正则序半群，A是S的有边界值（α，β）的直觉模糊左理想.对∀x∈S，存在a，b∈S，使得x≤ax2b.于是

［1］ Zadeh L A.Fuzzy Sets［J］.Inform.and Control，1965（8）：338－353.

［2］ Rosenfeld A.Fuzzy Groups［J］.J.Math.Anal.Appl.，1971，35（1）：512－517.

［3］ Kuroki N.On fuzzy ideals and fuzzy bi－ideals in semigroups［J］.Fuzzy Sets Syst.，1981（52）：203－205.

［4］ Kehayopulu N， Tsingelis M.Fuzzy sets in ordered groupoids［J］.Semigroup Forum，2002（65）：128－134.

［5］ Kehayopulu N，Tsingelis M.Regular ordered semigroups in terms of fuzzy subsets［J］.Inform.Sci.，2006（176）：3675－3693.

［6］ Zhan J，Dudek W A.Fuzzy h－ideal of hemir－ings［J］.Inform.Sci.，2007，177（3）：876－886.

［7］ Yin Y Q，Li H.The characterizations of h－hemiregular hemirings and h－intra－hemiregular hemir－ings［J］.Inform.Sci.，2008，178（17）：3451－3464.

［8］ Huang X K，Li H J，Yin Y Q.The h－hemiregular fuzzy duo hemirings［J］.International Journal of Fuzzy Systems，2007，9（2）：105－109.

［9］ Atanassov K T.Intuitionistic fuzzy sets［J］.Fuzzy Sets Syst.，1986（20）：87－96.

［10］ Biswas R.Intuitionistic fuzzy subgroups［J］.Math.Forum，1989（10）：37－46.

［11］ Kim K H，Jun Y B.Intuitionistic fuzzy ideals of semigroups［J］.Indian T.Pure Appl.Math.，2002，33（4）：443－449.

［12］ Dudek W A，Davvaz B，Jun Y B.On intuitionistic fuzzy sub－uasihypergroups of quasihypergroups［J］.Inform.Sci.，2005（170）：251－262.

［13］ Davvaz B，Dudek W A，Jun Y B.Intuitionistic fuzzy Hvsubmodules［J］.Inform.Sci.，2006（176）：285－300.

［14］ Khan A，Jun Y B，Shabir M.Ordered semigroups characterized by their intuitionistic fuzzy bi－ideals［J］.Iran.J.Fuzzy Syst.，2010（7）：55－69.

Intuitionistic Fuzzy Ideals with Thresholds of an Ordered Semigroup

HUANGXiaokun1，CHENGTao2
（1.College of Mathematics，Honghe University，Mengzi 661100，China；2.Department of Public Education，Yanjing Vocational College of Langfang，Langfang 065200，China）

The concept of intuitionistic fuzzy ideals with thresholds of an ordered semigroup is given and some related properties of it are studied.The intra－regularity of an ordered semigroup is characterized by use of the intuitionistic fuzzy soft left（right）ideals with thresholds of an intraregular ordered semigroup.

ordered semigroup；intuitionistic fuzzy left（right）ideals；complete lattice；intra－regular ordered semigroup

O 159

A

1008－9225（2012）02－0071－04

2011－11－28

国家自然科学基金资助项目（11161020）；云南省自然科学基金资助项目（2008CD186）.

黄晓昆（1979－），男，云南楚雄人，红河学院讲师.

刘乃义】