不同幅度噪声和缺失数据对大地电磁正则化反演的影响

李爱勇，曹创华，柳建新，郭荣文，童孝忠，柳 卓

(1. 中南大学 有色金属成矿预测教育部重点实验室，长沙 410083；2. 中南大学 地球科学与信息物理学院，长沙 410083；3. 有色金属华东地质勘查局，南京 210007)

自从物探反问题之父 BACKUS和应用数学家GILBERT提出了别具一格的 BG反演理论后，地球物理反问题成为地球物理学者研究的重要内容。在实际应用方面，地球物理勘探中最关键的一个环节就是如何进行数据处理，以便能有效地识别异常体；然而数据处理时的反演技术仍是解决实际问题的关键。大地电磁反演问题也往往可以转化为数学上不适定问题通过正则化方法求解，经过几十年来的发展，在地球物理的地震领域[1]、激电测井[2]、仪器仪表[3]、瞬变电磁测深[4]和垂直激电测深[6]领域基于正则化方法的反演已有所研究但实际应用效果还有待改进。正则化方法主要是利用改变正则化矩阵来改变反演的初始模型，然后进行最优化反演[7]。正则化反演初始模型的选择是否合理是反演结果的成败基础，在大地电磁领域，基于Wannamaker的正演模型成功实现了Occam的正则化反演[8]。

目前，国内外对于正则化初始模型的选择及其特点的分析较少，基本上是研究反演的过程，国内学者柳建新等[7]、陈小斌等[9]、童孝忠[10]系统分析了正则化大地电磁反演的现状，初步分析了基于混合遗传算法的正则化反演，但对如何选择最佳初始正则化模型以及在噪声影响和缺失数据下初始模型对反演效果的影响基本上没有讨论。本文作者针对地球物理正则化反演里常用的最平坦模型进行的计算，利用改变后的正则化矩阵分别讨论了最平滑模型和最小模型的反演效果，并进行了对比分析。然后就针对野外采集数据人文噪声难以避免的情况利用高斯噪声的形式加入到反演总体目标函数中进行了分析讨论。

此外，针对最平坦、最平滑和最小化模型的反演效果，选择这3种反演模型中较好的模型加入不同噪声，比较对于噪声的适应效果；然后针对某个频段或者深度的数据缺失时进行反演；最后讨论何种效果下的正则化反演是最适合在数据反演时利用。

1 大地电磁中的正则化反演技术

矿产地球物理勘探中，由于地形复杂，加之反演过程的复杂，结果往往不尽人意，会出现失真或者多解情况，这些情况在地球物理反演中被称为不适定问题。随着反演技术的发展，把非线性问题线性化，人们提出了广义线性化的处理手段。但是地球物理反演中的问题大多数是非线性的，并不是每种线性化中的理论都能用于广义的线性化反演，针对这种问题，很多学者提出了具有各自特色的方法来解决。总体上看，可以总结为求解不适定问题的一般方法，都利用一个数据集与原适定问题相近的解去逼近原始问题的解，统称为正则化方法[7]。

1.1 正则化的定义

正则化的定义是[11]：假设X、Y为Hilbert空间向量，T：X→Y是紧算子，T+无界，若Ra：Y→X是一族线性有界算子，有如下关系：

如果式(1)中α为正则化因子，则称Rα为算子T的正则化或正则化算子。

在实际问题中，方程 Tx=y的右端往往是观测到的值y，它与y之间存在误差，假设y ∈ D ( T+)，δδ且≤δ，Rαyδ作为方程Tx=y的精确解T+y的近似，其误差为

差，反映了Rα与T+之间的逼近程度。当α→0时，正则误差α→0时，

冗余误差被放大。从Rα逼近T+的角度来说，正则因子α越小越好；但从解的稳定性角度来说越小越好。这两方面是矛盾的，因此，必须合适选取正则参数α以获得较好的结果。

1.2 正则化因子的选取

目前，在地球物理反演当中，利用正则化方法来减少反演的多解性和增强过程的稳定性是最为有效的手段。正则化因子的选取直接影响着反演的结果，其值越合适，先验信息拟合的程度越高，就能更有效地利用野外所采集的数据。吴小平和徐果明[12]认为：在反演过程中可以选取一个折中化的因子，但这往往需要从外部输入，不断测算才能较好地符合我们想要的结果。CONSTABLE等[13]和 SMITH和 BOOKER[14]分别提出了Occam和RRI算法，这两种反演方法都能进行二维自适应的反演计算，其中Occam是利用线性搜索自适应迭代法选取最佳的正则化因子[8]，实现了数据充分拟合和模型极度光滑；RRI是通过所建立的反演函数中的目标项和自适应因子之间的关系[8]，根据每次得到的目标项来推测自适应因子。这两种反演算法已经用在了实际生产中，效果较好，但是遇到数据量很大时，就有些力不从心，尤其是原始数据比较粗糙时，更难解决。

正则化通过人为地强加某种结构信息(可以结合具体问题的结构特点)，在数学上为地球物理反演问题提供唯一的、稳定的结果。正则化因子的选择是正则化反演的关键，其值过大反演结果只包含先验正则化结构信息；过小则只包含数据反映的结构信息，因此，如何选取一个合适的正则化因子是非常重要的前提。目前，常用的正则化因子的求解方法有 GCV方法，L-Curve方法[10]和概率统计法，本文作者在加入噪声时的讨论中，采用的正则化因子的选择方法是位对噪声的Gaussian假设，其数据拟合服从Chi-square分布，属于概率统计方法。

2 正则化矩阵的选取及其反演效果

则有：

可以得到：

反演总体目标函数可以用下式进行表示[12,15−18]：

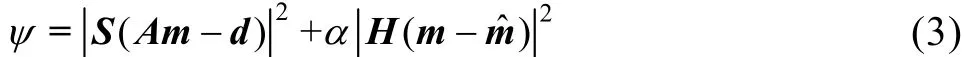
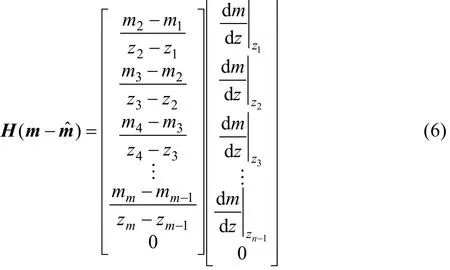
如果先验模型参数mˆ和不定的参数ξi，i=1，…，m都是可以加以利用，那么可以得到正则化矩阵如下：

设定数据和先验信息都是对称的矩阵，这意味着mˆ和标准差ξi伴随着假设模型先验参数的分解都是高斯分解法。如果已知的先验信息是比较好的，一般情况下，正则化因子都被设定为α=1。这种情况下的参数设定不只是依赖于χ2(即数据拟合服从Chi-square分布)变化的。在这种情况下，即使估计的参数不确定，但通过奇异值分解的反演效果来看，与零估计相比可能仍然是比较好的选择。

2.1 3种正则化矩阵初始模型

2.1.1 最平坦模型正则化

模型m代表着一个m(z)空间函数的一个分量，假设 0=m 和

最平坦模型是指使的函数

H ( m − m ˆ)2的梯度利用拉格朗日法求取最小值时，仍然尽可能地拟合原始模型。如果Zi+1−Zi=Δ为常数，那么得到的矩阵如下：

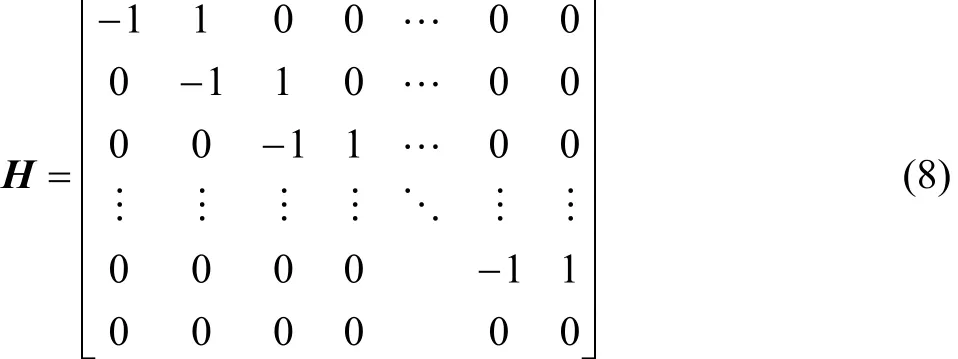
式(8)即为最平坦模型正则化矩阵。2.1.2 最平滑模型正则化

正则化矩阵 H 能被离散成对角矩阵的形式(式(9))：

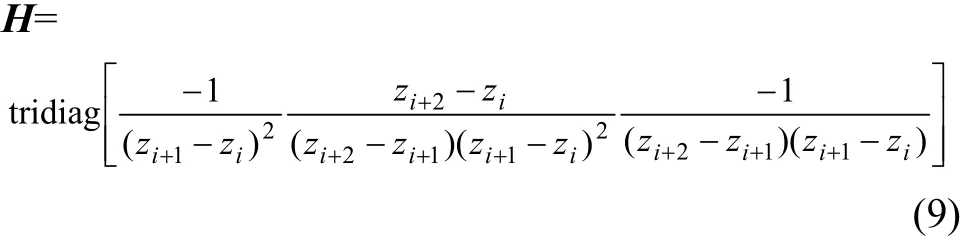
在其底部最后两行为零。如果无法先验知道基模型mˆ的结构信息，可以假设mˆ=0，那么可以得到

这种加入了二阶偏导数先验信息称之为最平滑模型正则化反演。

如果令Zi+1−Zi=Δ为常数，则有：

式(11)即为最平滑模型正则化矩阵。2.1.3 最小模型正则化

最小正则化模型的定义是假设H=I和m=0，其中I表示单位矩阵，然后再带入反演目标函数进行正则化计算，也被称为零阶正则化阻尼最小二乘方法，其具体的实现过程如下：

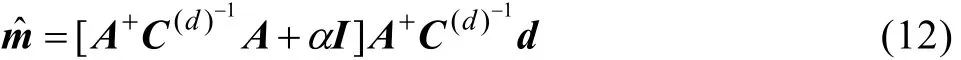
给定生成矩阵的主对角线乘以正则化因子α，用以克服其奇异性或者改善病态条件。

令：

即得：

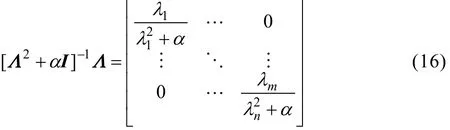
根据 2.1节提到的正则化初始模型，利用正则化算法和2D海洋电磁Occam反演原理[8]，通过对正则化矩阵初始的修正，针对上述加入3种不同幅度噪声，反演结果分别如2.2.1～2.2.3小节所述，其中3种情况下的反演结果如图1～3所示。

2.2.1 最平坦模型

如图1所示，当深度为0～700 m时，加入3种不同噪声后反演所得电阻率均为20 Ω·m左右；当深度为700～2 000 m时，只有加入0.02%的噪声时，反演所得电阻率为10 Ω·m左右，而噪声变大时，会掩盖此信息；当深度为2 000～3 500 m时，随着噪声的增加，反演

求得其最大值λi，有

2.2 不同噪声下的反演

对表 1中一维地层模型产生的合成数据(虽然误差不切合实际，但可以更好地研究和分析地球物理反演问题)加入0.02%、2%、20%的噪声，然后研究这3种情况下的正则化反演结果。结果越来越偏离真实结果；当深度趋于无限大时，反演结果都趋于地表表层电阻率，低于初始模型设置的电阻率。由此可见，噪声为 0.02%时，由于噪声干扰小，结合先验信息可以很好地反演、重构实际模型。随着数据噪声的增大(干扰信号的增加)，反演结果越来越差；当噪声达到20%时，反演结果完全不能反映真实情况。这时反演结果大部分信息来自于最平整结构信息(即所有相邻参数间的变化率为最小)。因此，数据误差较大时，即便对于简单模型也很难重构实际的模型结构。从这些方面来看，在进行野外实测数据时，应尽量选用信噪比高的物探仪器，采用必要的措施减少数据误差，这样才有利于更好地反演野外数据。2.2.2 最平滑模型

表1 层状合成模型参数Table 1 Parameters of layer model

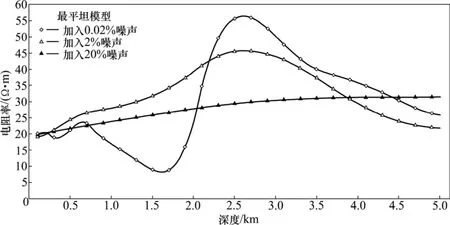
图1 加入不同噪声最平坦模型反演结果拟合图Fig. 1 Inversion fitting diagram of different noise with flattest model

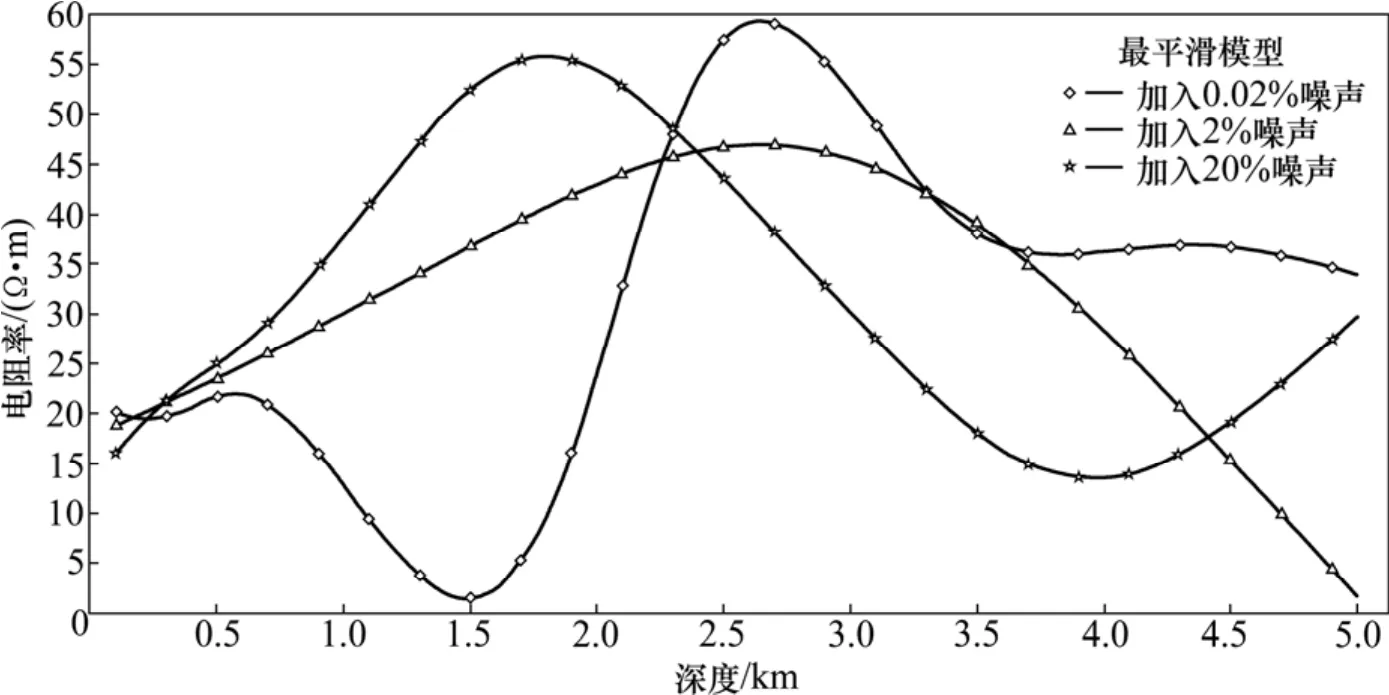
图2 加入不同噪声最平滑模型反演结果拟合图Fig. 2 Inversion fitting diagram of different noise with the smoothest model

图3 加入不同噪声最小模型反演结果拟合图Fig. 3 Inversion fitting diagram of different noise with the smallest model

如图2所示，当深度为0～700 m时，加入3种不同噪声后反演所得电阻率均为20 Ω·m左右，最平坦模型和最平滑模型具有相似的特点。当深度为 700～2 000 m时，加入0.02%的噪声后，反演所得电阻率出现接近0 Ω·m的情况；加入2%的噪声后，反演所得电阻率几乎为模型电阻率的2倍；而加入20%的噪声后，反演所得电阻率已达模型电阻率的2倍以上；当深度为2 000～3 500 m时，加入0.02%的噪声后，反演结果基本上符合真实值，而加入其他两种噪声后，反演结果都低于50 Ω·m；当深度趋于无限大时，反演结果都趋于地表表层电阻率；加入20%的噪声后，反演所得电阻率趋于0 Ω·m。同样，可以得到与最平坦模型相似的结果，随着噪音的增加，曲线越来越不符合初始模型。当噪声足够小时，可以有效地反演出模型结构信息；随着数据噪声的增大(干扰信号的增加)，反演结果越来越差。当噪声达到20%时，反演结果完全不能反映真实电性结构。这时反演结果大部分信息来自于最平滑结构先验信息(即所有相邻参数间的二阶偏导数最小)。与最平坦模型不一样的是，最平滑反演后的结果更倾向于二次光滑结构。

2.2.3 最小模型

图3所示，当深度为0～700 m时，加入3种不同噪声后反演所得电阻率变化较大，曲线直上直下，都在20 Ω·m左右振荡；当深度为700～2 000 m时，加入3种噪声后，曲线都是递减函数，3种情况相似，都从40 Ω·m 降到 10 Ω·m左右；当深度为 2 000～3 500 m时，加入 0.02%的噪声后，反演结果基本上符合真实值，而加入其他两种噪声后，反演结果都低于50 Ω·m，曲线的斜率都很小；当深度趋于无限大时，加入 0.02%的噪声后，反演结果趋于地表表层电阻率，而加入2%和20%的噪声后，反演结果相似，趋于30 Ω·m左右。总体上看：随着噪声的增加，最小化模型的适应性越来越差，但是这种模型不像最平坦模型和最平滑模型那样明显受数据误差的影响，它仍然可以反映真实模型的一些信息。因此，在以上3种反演方法中，最小化模型反演受数据误差的影响程度最小。

2.3 “信息不完全”下的反演

当模型结构信息“不完全”(即缺失数据时)或灵敏度矩阵病态时，为了研究以上3种正则化反演法的反演特点以及处理这些情况的方式，还是采用表1的模型实例，并在产生的反演数据中加入0.01%的噪声。为了方便研究，通过以下等效方式模拟数据信息的不完全(即缺失数据时)或灵敏度矩阵的病态：在本例反演中，将灵敏度矩阵中部分列元素删除掉用以表示电磁响应后所得数据缺失。反演结果如图4所示。

如图4所示，当深度为0～700 m时，3种正则化模型反演所得结果都很好，均为首层电阻率20 Ω·m左右；当深度为700～2 000 m时，最平滑模型和最平坦模型反演结果为10 Ω·m左右，而最小模型反演结果基本上与首层分不清，为20 Ω·m左右，分辨率较低；当深度为2 000～3 500 m时，最平滑模型和最平坦模型反演结果都是50 Ω·m左右，曲线圆滑，而最小模型在缺失数据时，相对高阻变为0 Ω·m左右；当深度趋于无限大时，3种正则化反演初始模型反演结果形态相似，都为40 Ω·m左右，较为真实。由以上分析可知，对于最平坦模型反演，可采用线性插值相邻反演结构来获得缺失信息部分的信息；对于最平滑模型反演，只是按照相邻节点信息圆滑了缺失的数据；对于最小化模型反演，只采用了基模型m=0的信息。从以上反演结果可知，当某部分结构信息在数据中反映不明显时，这3种模型在反演中对这些情况的处理方式不一样。但是具体哪种正则化反演效果好，需要具体问题具体分析，比如对于连续的大地地电参数反演，最平坦模型和最平滑模型的反演效果可能会好些，而最小化模型的反演效果可能较差。

3 结论

1) 选择合适的正则化反演初始模型，对反演结果的影响至关重要，最平坦模型和最平滑模型反演效果较好，最小化模型反演效果一般。

2) 噪声信息在反演中的影响起着决定作用，对于最平坦模型，噪声较小时反演效果最好，随着噪声的增加，反演效果逐渐变差；对于最平滑模型，噪声较小时反演效果很好，基本跟模型十分吻合，但随着噪声的增加，跳变比最平坦模型变化复杂，不能正确的反映初始模型；对于最小化模型，不管噪声多大，反演效果都不理想。

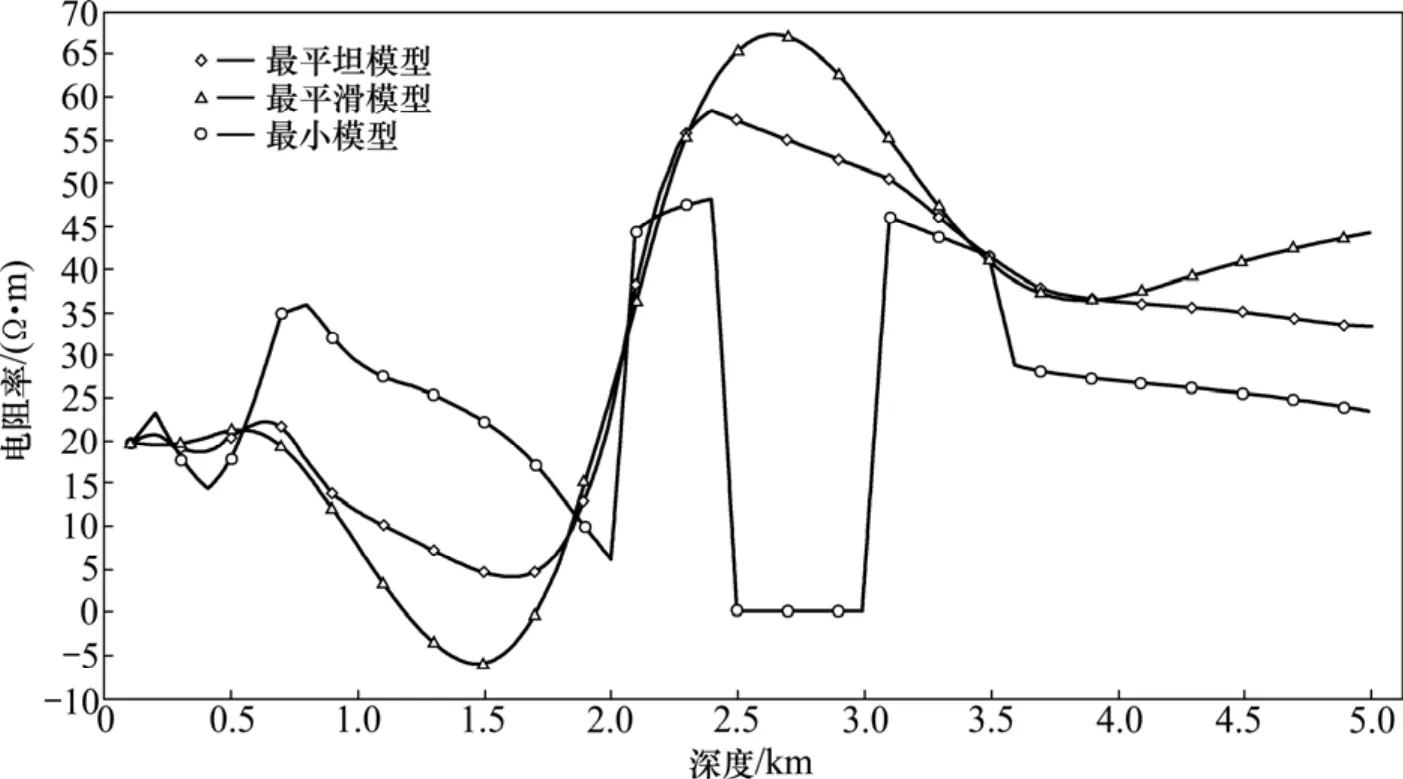
图4 信息“不完全”加入0.01%噪声时3种正则化模型反演结果图Fig. 4 Fitting diagram of regularization inversion with three missing data model by 0.01% noise

3) 缺失数据信息时，各种初始化模型在噪声较小的情况下，均能反映真实的地电断面情况，只是最小化模型反演出的数据跳变很大，有时难以辨认其真实特征。

致谢：

本文成文过程中得到了“有色资源与地质灾害探查”湖南省重点实验室全体成员的协助，在此表示最衷心的谢意。

[1] 王振宇, 刘国华. 走时层析成像的迭代 Tikhonov正则化反演研究[J]. 浙江大学学报: 工学版, 2009, 37(12): 1685−1690.

WANG Zhen-yu, LIU Guo-hua. Study of travel time tomography by iterative Tikhonov regularization inversion [J].Journal of Zhe Jiang University: Engineering Science, 2009,37(12): 1685−1690.

[2] 汪宏年, 陶宏根, 其木苏荣, 杨善德. 水平层状介质中双侧向资料的全参数正则化迭代反演与应用[J]. 地球物理学报,2002, 45(增刊): 387−399.

WANG Hong-nian, TAO Hong-gen, QI Mu-su-rong, YANG Shan-de. Regularized entire-parameter iterative inversion of dual-later log in horizontally stratify flied media and its application [J]. Chinese Journal of Geophysics, 2002, 45(Suppl):387−399.

[3] 郝燕玲, 成 怡, 孙 枫, 刘繁明. Tikhonov正则化向下延拓算法仿真实验研究[J]. 仪器仪表学报, 2008(3): 225−228.

HAO Yan-ling, CHENG Yi, SUN Feng, LIU Fan-ming.Tikhonov regularization downward continuation algorithm simulation experimental study [J]. Chinese Journal of Scientific Instrument, 2008(3): 225−228.

[4] 毛立峰, 王绪本, 陈 斌. 直升机航空瞬变电磁自适应正则化一维反演方法研究[J]. 地球物理学进展, 2011, 26(1):300−305.MAO Li-feng, WANG Xu-ben, CHEN Bin. Study on an adaptive regularized 1D inversion method of helicopter TEM data [J]. Progress in Geophysics, 2011, 26(1): 300−305.

[5] 刘海飞, 柳建新, 阮百尧, 张赛民. 垂直激电测深二维自适应正则化反演[J]. 同济大学学报: 自然科学版, 2009, 37(12):1685−1690.

LIU Hai-fei, LIU Jian-xin, RUAN Bai-yao, ZHANG Sai-min.2D self adaptive regularization inversion with vertical induced polarization sounding data [J]. Journal of Tongji University:Natural Science, 2009, 37(12): 1685−1690.

[6] WANNAMAKER P E, STODT J A, RIJO L. Two-dimensional topographic responses in magnetotelluric model using finite elements [J]. Geophysics, 1986, S1: 2131−2144.

[7] 柳建新, 孙 娅, 郭荣文, 童孝忠, 王 浩, 郭振威. 基于TSVD求解大地电磁不适定反演问题[J]. 中国科技论文在线,2009, 21(2): 2284−2290.

LIU Jian-xin, SUN Ya, GUO Rong-wen, TONG Xiao-zhong,WANG Hao, GUO Zhen-wei. Based on TSVD algorithm to solve the ill-posed inversion of magnetotelluric problems [J].China Science Paper Online, 2009, 21(2): 2284−2290.

[8] WANNAMAKER P E. Occam2DMT [EB/OL]. [2011−03−15].http://marineemlab.ucsd.edu/occam.

[9] 陈小斌, 赵国泽, 汤 吉, 詹 艳, 王继军. 大地电磁自适应正则化反演算法[J]. 地球物理学报, 2005, 48(4): 937−946.

CHEN Xiao-bin, ZHAO Guo-ze, TANG Ji, ZHAN Yan, WANG Ji-jun. Magnetotellurics adaptive regularized inversion algorithm[J]. Chinese Journal of Geophysics, 2005, 48 (4): 937−946.

[10] 童孝忠. 大地电磁测深有限单元法正演与混合遗传算法正则化反演研究[D]. 长沙: 中南大学, 2008: 70−104.

TONG Xiao-zhong. Research of forward using finite element method and regularized inversion using hybrid genetic algorithm in magnetotelluric sounding [D]. Changsha: Central South University, 2008: 70−104.

[11] 朱华平. 不适定问题的正则化理论及其应用[D]. 武汉: 武汉理工大学, 2007: 10−32.

ZHU Hua-ping. Regularization theory and its application [D].Wuhan: Wuhan University of Technology, 2007: 10−32.

[12] 吴小平, 徐果明. 大地电磁数据的 Occam 反演改进[J]. 地球物理学报, 1998, 41(4): 547−554.

WU Xiao-ping, XU Guo-ming. The Occam inversion of magnetotelluric data [J]. Chinese Journal of Geophysics, 1998,41(4): 547−554.

[13] CONSTABLE SC, PARKERRL, CONSTABLE C G. Occam’s inversion: A practical algorithm for generating smooth models from electromagnetic sounding data [J]. Geophysics, 1987, 52(3):289−300.

[14] SMITH J T, BOOKER J R. Rapid inversion of two- and three-dimensional magnetotelluric data [J]. Geophysics, 1991, 96:3905−3992.

[15] 傅淑芳, 朱仁益. 地球物理反演问题[M]. 北京: 地震出版社,1998: 1−67.

FU Shu-fang, ZHU Ren-yi. The geophysical inversion problem[M]. Beijing: Earthquake Press, 1998: 1−67.

[16] 杨文采. 地球物理反演的理论与方法[M]. 北京: 地质出版社,1996: 1−112.

YANG Wen-cai. Theory and method of geophysical inversion[M]. Beijing: Geological Publishing House, 1996: 1−112.

[17] 汤井田, 任政勇, 化希瑞. 地球物理学中的电磁场正演与反演[J]. 地球物理学进展, 2007, 22(4): 1181−1194.

TANG Jing-tian, REN Zheng-yong, HUA Xi-rui. Electromagnetic forward modeling and inversion in geophysical [J].Progress in Geophysics, 2007, 22(4): 1181−1194.

[18] 吉洪诺夫·A·N, 阿尔先宁·V·Y. 不适定问题的解法[M].王秉枕译. 北京: 地质出版社, 1979: 1−221.

TIKHONOV A N, ARSENIN V Y. Ill-posed problem solution[M]. WANG Bing-zhen, transl. Beijing: Geological Publishing House, 1979: 1−221.