改进BISQ模型地震波场数值模拟中的边界处理
2012-11-24周竹生
周竹生,王 红
(1. 中南大学 有色金属成矿预测教育部重点实验室,长沙 410083;2. 中南大学 地球科学与信息物理学院,长沙 410083)
改进BISQ模型地震波场数值模拟中的边界处理
周竹生1,2,王 红1,2
(1. 中南大学 有色金属成矿预测教育部重点实验室,长沙 410083;2. 中南大学 地球科学与信息物理学院,长沙 410083)
从改进BISQ模型双相介质所对应的一阶速度—应力运动方程出发,构建2×2N阶交错网格有限差分模拟算法,为了尽可能地减小或消除数值模拟中由人工边界引起的虚假反射,建立完全匹配层(PML)吸收边界的2×2N阶交错网格有限差分算法。详细地讨论了PML吸收边界条件的构建及其有限差分算法的实现。通过MATLAB编程进行波场模拟,将加入PML吸收边界、常规指数衰减吸收边界及未加吸收边界的3种数值模拟结果进行对比,论证PML吸收边界能十分有效地吸收边界反射。
改进BISQ模型;双相介质;有限差分;交错网格;完全匹配层(PML)
相对单相介质而言,双相介质能够更好地描述实际地层结构和性质,因此,双相介质的数值模拟更有利于实际介质中的地震波传播规律的认识和研究[1-4]。在利用计算机进行数值模拟计算过程中,由于计算区域有限,在波动方程数值模拟中常出现的问题就是来自边界的人工反射,这种反射是由缩小计算区域而引起的。避免边界反射的最简单的方法是增大计算区域,但这种方法会延迟边界反射和超出模拟的最大时间,显然增加了计算量[5]。因此,出现了其它避免边界反射的方法,例如吸收边界条件。
好的吸收边界条件不仅要吸收效果好,而且边界应能尽量贴近主要计算区域,这样可以节约计算机存储空间和计算时间。计算吸收边界的方法有很多种。最早的吸收边界条件是由Lysmer和Kuhlemeyer提出的[6],常被称为黏性边界条件,它的缺点是吸收人工反射波的效果较差。使用最为普遍的是CLAYTON和ENGQUIST[7],ENGQUIST 和 MAJDA[8]提出的二维吸收边界条件,他们用拟微分算子的工具将波动算子作分解,在人工边界上保留向外传播的部分,然后用Pade逼近,得到不同精度的边界微分方程。这种边界条件能完全吸收垂直入射时的反射波,且二阶以上的Clayton-Engquist条件能较好吸收入射角在一定范围内的反射波,但当入射角接近π/2时,吸收效果很不好。虽然旁轴近似法[9]实现起来比较简单且需要的网格数较少,能完全吸收垂直入射时的反射波,同时能较好吸收入射角在一定范围内的反射波,但它只在一定的角度和频率范围内是有效吸收的。
针对上述不足,本文作者拟采用完全匹配层(PML)吸收边界法来进行边界处理,并通过计算实例,将其与传统的指数衰减法进行对比,据此说明 PML方法的有效性。
1 数值模拟中的交错网格高阶有限差分
在改进BISQ模型的双相介质地震波场数值模拟中采用的一阶速度—应力方程[10]为

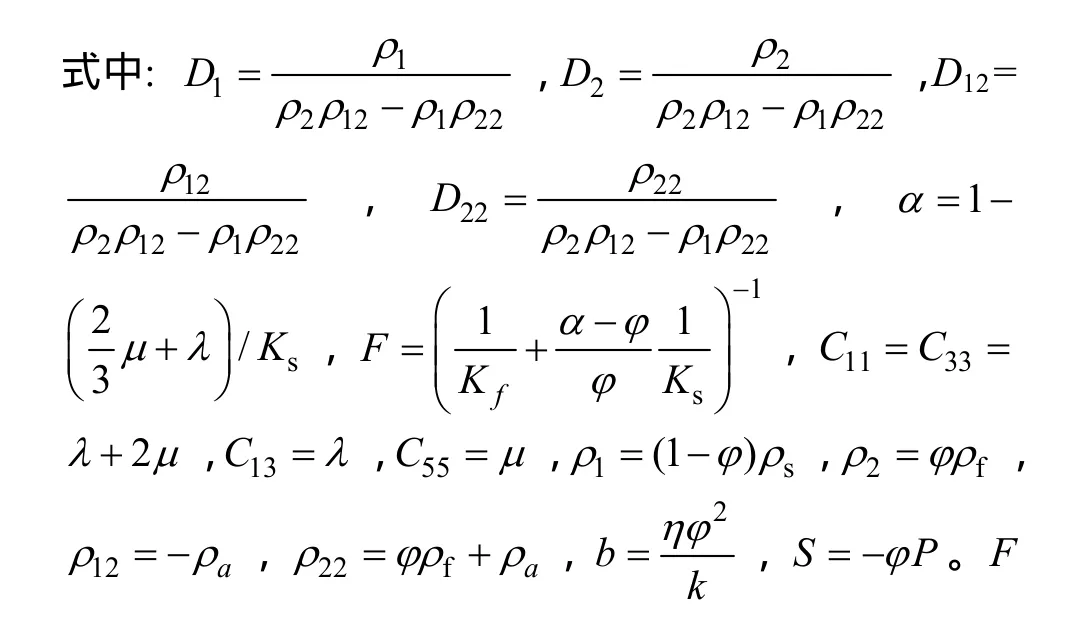
称为Biot流系数;Ks为固体体积模量;流体体积模量Kf可由流体声速来确定;α为有效应力的孔隙弹性系数;vx、vz、Vx和 Vz分别表示固体和流体的位移分量;xxσ、zzσ分别是固体x、z方向的正应力;xzσ是固体的切应力;sρ和fρ分别为固体和流体密度;φ为孔隙度;η为流体黏滞系数;aρ为固-流耦合附加密度;μ和λ为弹性常数;k为渗透率;P为流体压力。
对方程(1)进行高阶差分近似,所构建的空间 2N阶、时间2阶精度的有限差分格式如方程(2)所示,其他方程的差分格式与此类似。其中i、j、k表示x、z、t的离散序号;U、W、P、Q和S分别表示固相vx、vz、σxx、σzz和 σxz;u、w、F 和 R 分别表示流相 Vx、Vz、S 和 P。
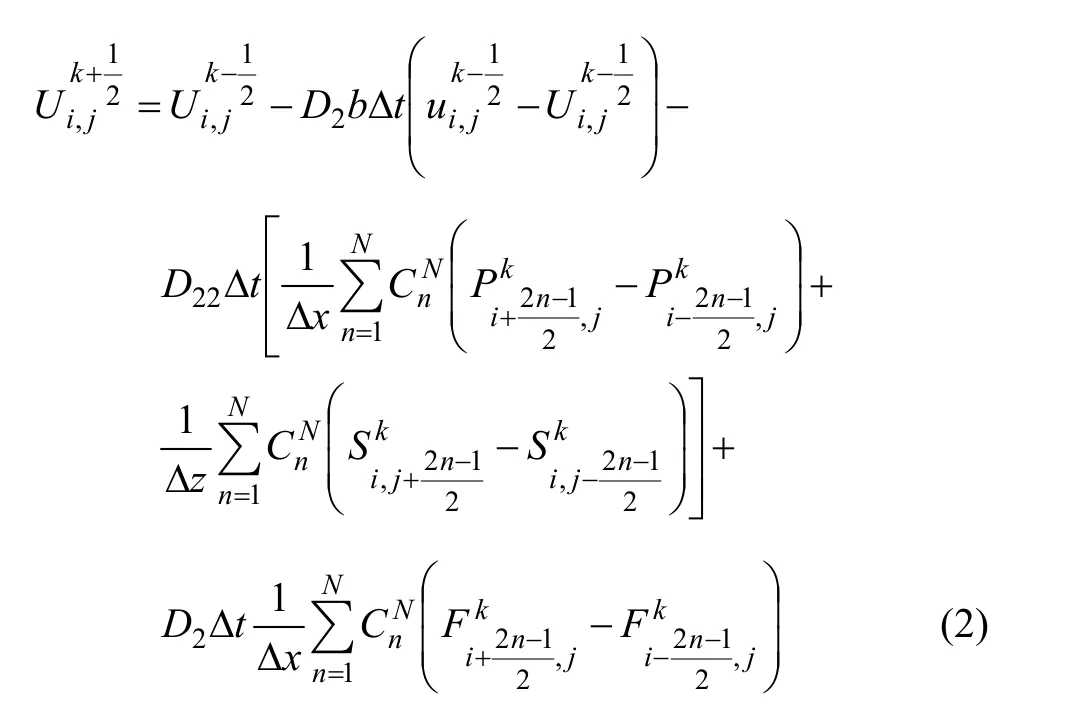
2 边界条件
2.1 指数衰减边界条件
指数衰减的原理是对网格周围的耗散采用质点的速度和应力值同乘上一个小于1的函数来衰减。例如,采用CERJAN等[11]建议的吸收边界,则吸收衰减函数定为
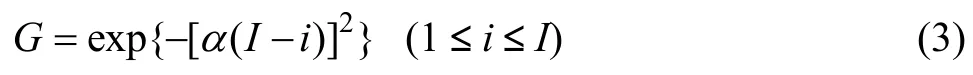
式中:I为给定的吸收边界带宽度的节点数;i为吸收边界内的节点号;α为衰减系数,其值的选定与I的大小密切相关,且对吸收效果的影响很大。这种吸收衰减方法的特点是对每个方向的反射波都采取相同的处理方式,实施方便简单,计算所占内存小。缺点是给定的吸收介质的边界要宽,不允许靠近边界的区域出现介质的不连续性,计算精度不高,吸收效果较一般。
2.2 PML边界条件
完全匹配层(PML)的概念由Berenger于1994年首先提出[12],它是目前消除边界反射的理想方法之一。最初它被运用于时域电磁场有限差分边界问题的解决中,后来人们不断将其推广到其他领域,并在声波与弹性波的地震波数值模拟中得到成功应用[13-16]。PML吸收边界条件假设存在一种各向异性有耗介质(PML层),地震波进入PML层后迅速衰减,通过适当选取参数,能够使以不同入射角进入边界层的任意频率和任意极化的地震波保持其特征阻抗和相速度均固定,从而使地震波能够完全匹配自由空间,理论上不产生任何反射[17-19]。
下面运用分裂式方法来实现完全匹配层(PML)思想,并给出相应的差分格式。
图1所示为PML吸收边界的区域划分示意图,其中,区域A1、A2、A3、A4分别为左边界、右边界、顶边界和底边界,区域 B1、B2、B3和 B4分别代表四个角区域,区域C是模拟工作的主要计算区域。
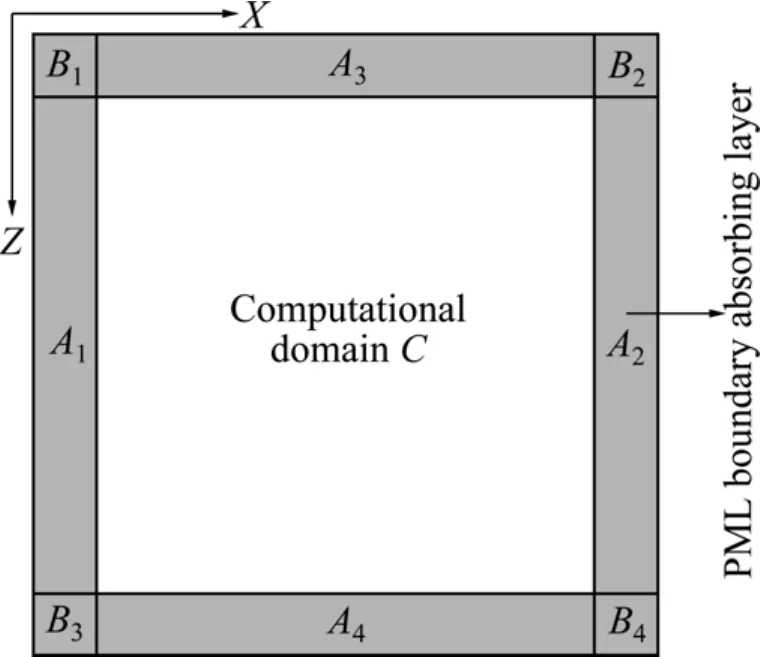
图1 PML吸收边界区域划分示意图Fig. 1 PML absorbing boundary zoning diagram
PML介质中存在8个分量,在进行边界条件处理时,需要对每个方向上的分量沿界面垂直和平行两个方向进行分裂,为了消除人工分界面上的反射,在界面的垂直方向上需引入吸收衰减系数。
在二维空间条件下,对一阶速度—应力弹性波动方程运用时域变量分裂法,对 PML介质中的每个分量进行波场变量分离,并对于每个波场变量分裂如下:

展开为

式中:上标x和z代表相应的空间导数。根据上式对方程组(3)进行分裂,得到带有衰减因子的 PML吸收边界系统方程组的差分格式如下:
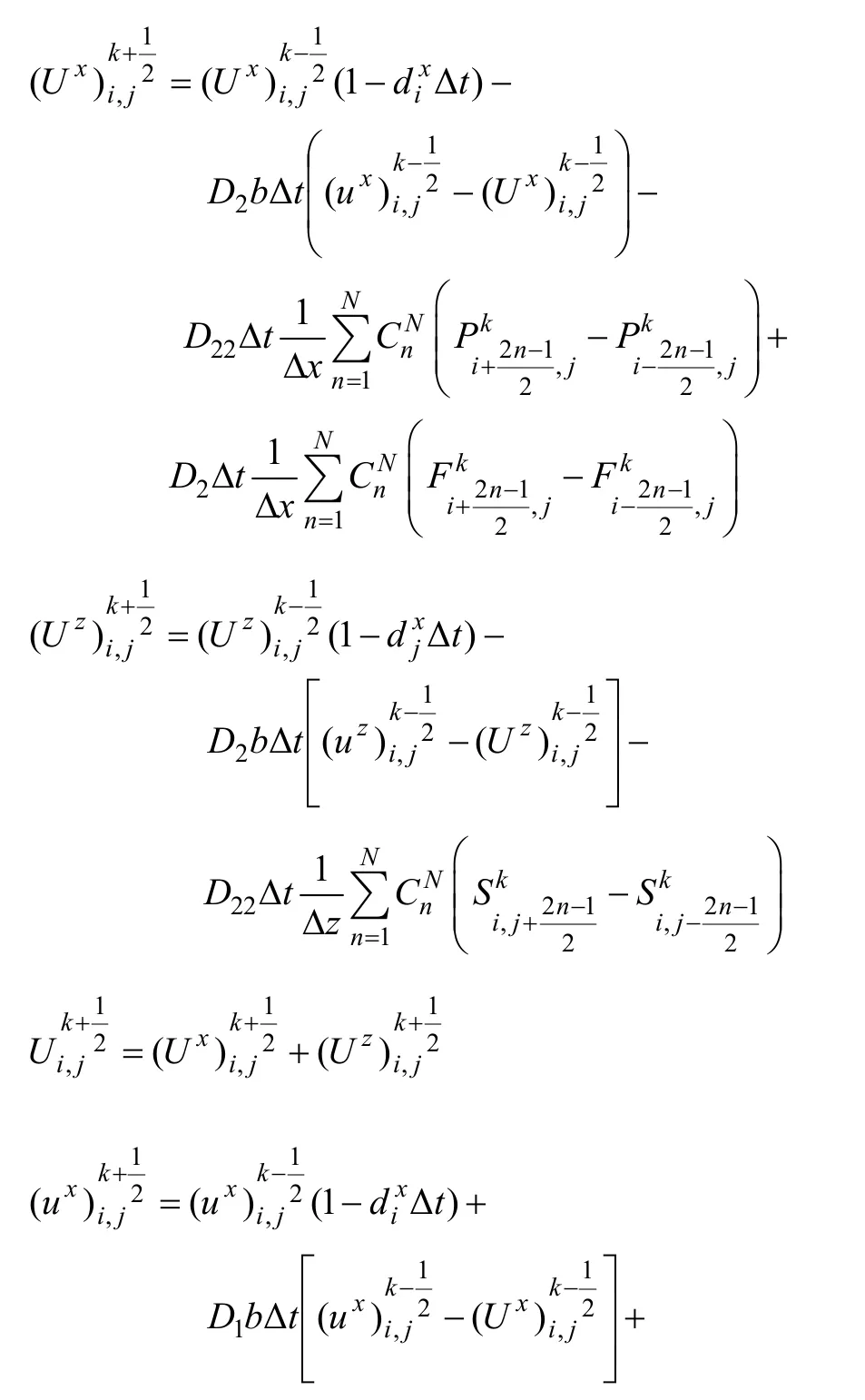
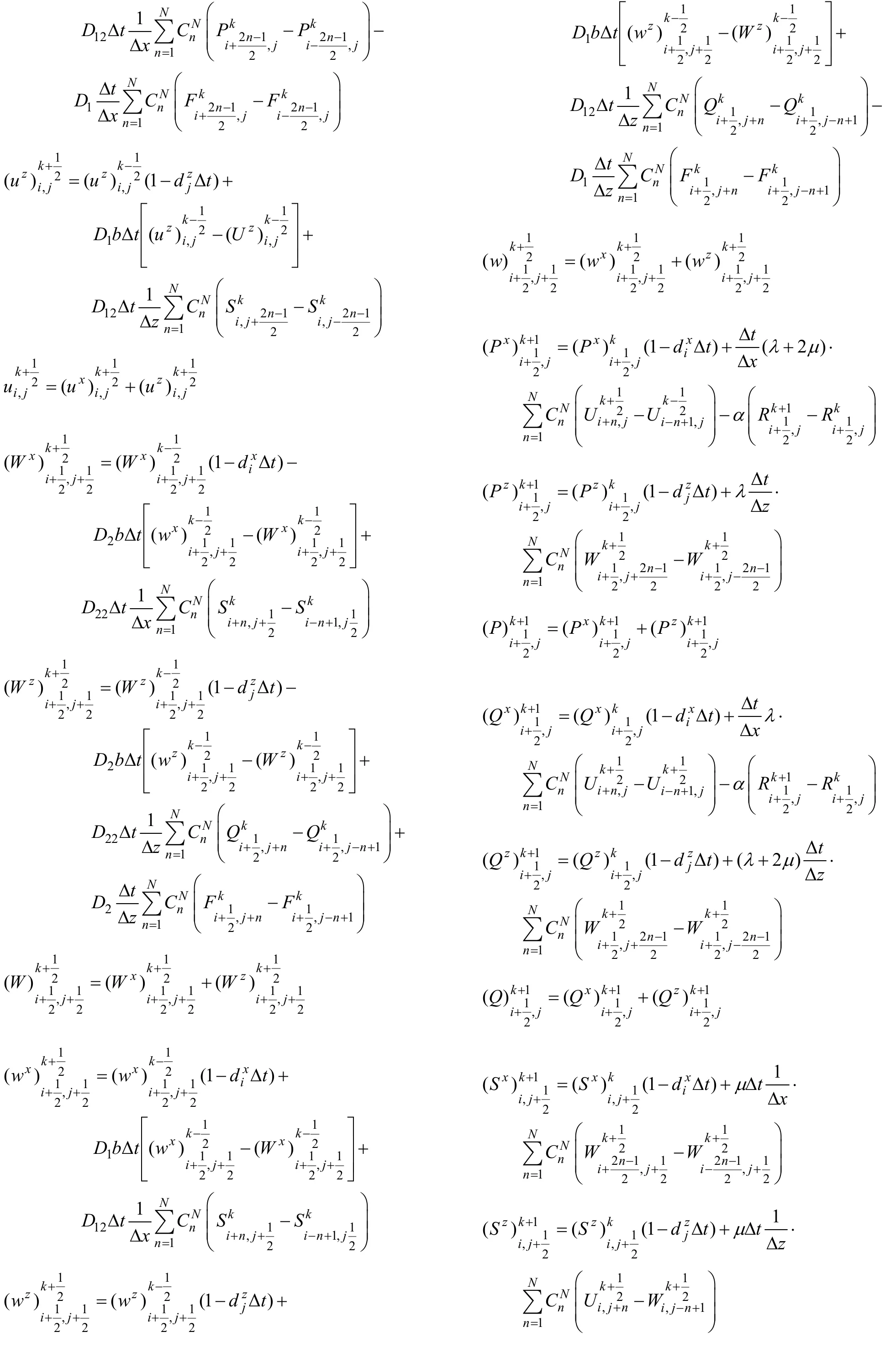
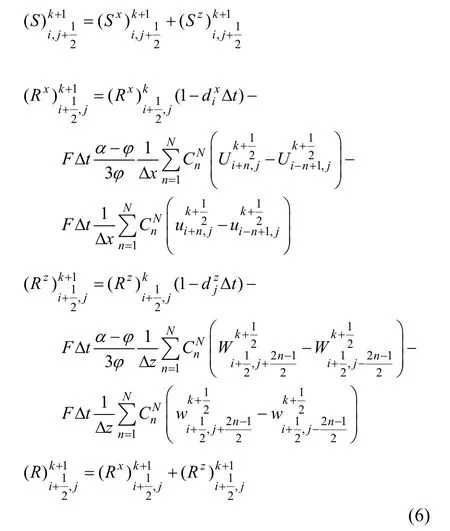
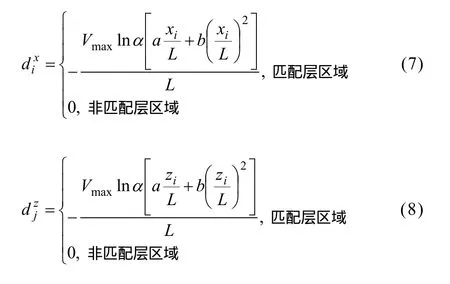
式中:Vmax代表PML介质层的速度(最大纵波速度);α= 10-6代表理论反射系数;L代表匹配层宽度;xi为匹配层区域与内部区域界面的横向距离;zi为匹配层区域与内部区域界面的纵向距离;系数a=0.25,b=0.75。
数值模拟计算时,衰减系数的取值根据其所在的区域变化而改变,在不同区域其取值不同。根据图1,在左边界A1和右边界A2区域:>0,=0;在上边界A3和下边界A4区域:=0,>0;在四个角B1、B2、B3、B4区域:>0,>0。
3 波场模拟
为检验模拟算法的正确性,本文作者建立了一个各向同性双相介质模型,模型网格点数为200×200,网格间距为5 m,时间间隔为0.1 ms,震源位于模型中心,采用主频为30 Hz的雷克子波,模型的物性参数设置如下:固体参数有拉梅系数12.72 GPa,剪切模量 6.84 GPa,固体体积模量 56.81 GPa,密度 2 738 kg/m3,耦合附加密度83 kg/m3,纵波速度3 000 m/s,横波速度2 000 m/s;流体参数有体积模量1.46 GPa,密度454 kg/m3,孔隙度0.237 8,粘滞系数1×10-6Pa·s,渗透率10 md。采用精度为O(Δt2+Δx16)的交错网格有限差分法,对固体和流体的水平分量和垂直分量分别进行计算,数值模拟的结果如图2所示。
由图2可以看出,在双相介质中存在第二类纵波,从内到外依次为慢纵波(p),横波(S)和快纵波(P),其衰减规律明显不同于第一类纵波,第一类纵波在固相和流相都引起较强的振动,第二类纵波引起较弱的固相振动,较强的流相振动,这种关系取决于双相介质的性质。其中第一类纵波的相位在固相和流相部分是相同的,第二类纵波的相位在固相和流相部分则相反。
4 边界处理效果对比
根据以上模型,对固体和流体的水平分量和垂直分量分别进行计算,并采用不同方法对人工边界进行处理,所得数值模拟结果如下(见图3~5):
图3所示为对人工边界未进行任何处理时所得到的150 ms时刻的波场快照。由图3可见,在边界处,产生了明显的边界反射波,必将严重干扰计算波场的记录特征。
图4所示为对人工边界采用了指数衰减处理时所得到的150 ms时刻的波场快照,此时,边界反射波明显减弱,有效波场得到突出,但边界反射很难吸收干净,对计算波场仍存影响。
图5所示为对人工边界采用了PML吸收边界条件处理后所得到的 150 ms时刻的波场快照。从图 5可清楚看出,加了 PML吸收边界以后,由于该边界条件很好地削弱了来自人工边界的反射,使得模拟波场的特征变得非常清晰。
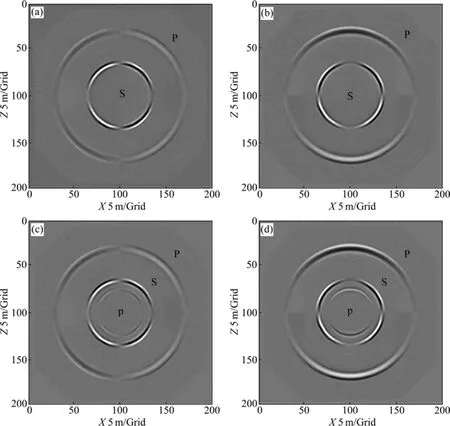
图2 100 ms时刻的波场快照(时间2阶,空间16阶)Fig. 2 Snapshots of 100 ms (two-order time and sixteen-order space): (a) Solid phase horizontal components; (b) Solid phase vertical components; (c) Flow phase horizontal components; (d) Flow phase vertical components
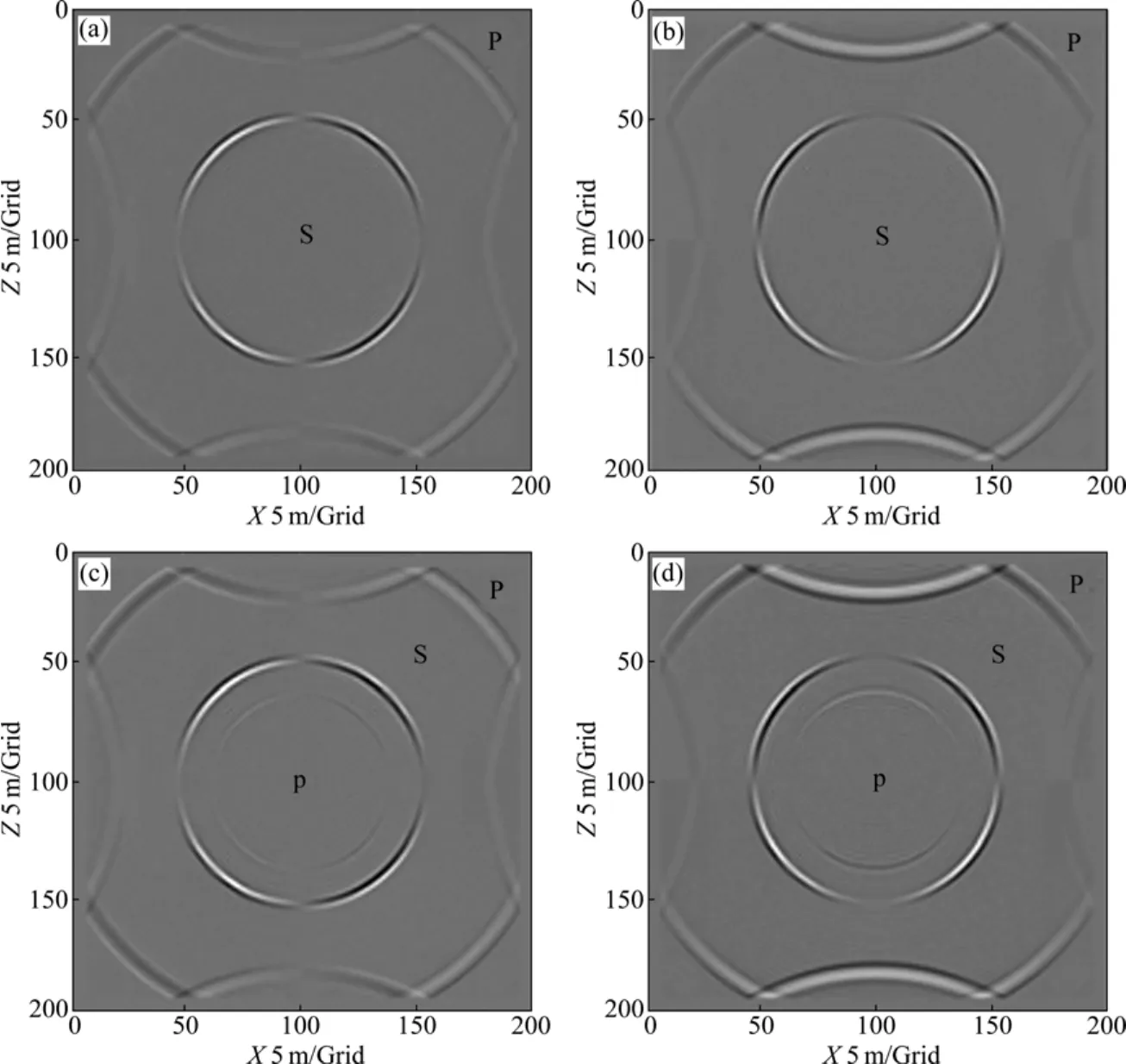
图3 未加边界条件时150 ms时刻的波场快照(时间2阶,空间16阶)Fig. 3 Snapshots of 150 ms (two-order time and sixteen-order space) with non-absorbing boundary: (a) Solid phase horizontal components; (b) Solid phase vertical components; (c) Flow phase horizontal components; (d) Flow phase vertical components
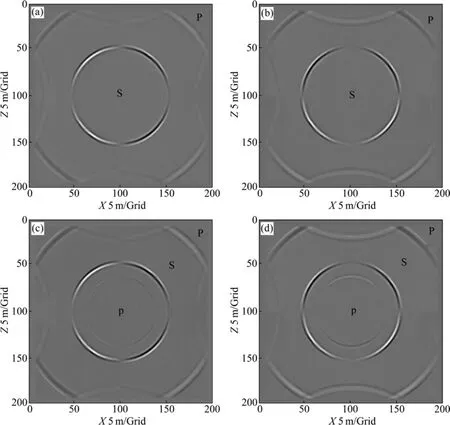
图4 加指数衰减边界时150 ms时刻的波场快照(时间2阶,空间16阶)Fig. 4 Snapshots of 150 ms (two-order time and sixteen-order space) with exponential boundary: (a) Solid phase horizontal components; (b) Solid phase vertical components; (c) Flow phase horizontal components; (d) Flow phase vertical components
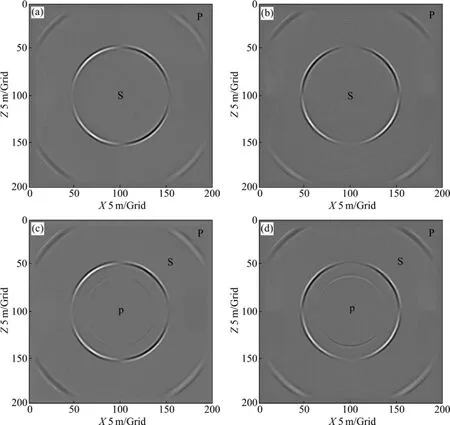
图5 加PML边界条件时150 ms时刻的波场快照Fig. 5 Snapshots of 150 ms (two-order time and sixteen-order space) with PML: (a) Solid phase horizontal components; (b) Solid phase vertical components; (c) Flow phase horizontal components; (d) Flow phase vertical components
5 结论
1) 将交错网格有限差分法运用于改进BISQ模型的双相介质,给出了其相应的一阶速度—应力波动方程在不同时间和空间精度条件下的交错网格差分算法格式,实现了双相介质的地震波场数值模拟。模拟波场符合双相介质的理论特征,表明所建立的算法格式是正确、可行的。
2) 针对波场数值模拟过程中的边界处理问题,建立了完全匹配层(PML)边界的2×2N阶交错网格高阶有限差分格式,通过与未加吸收边界及加常规指数衰减吸收边界所得到的模拟波场进行对比,说明 PML边界条件能十分有效地吸收边界反射,验证了 PML吸收边界条件的高效、优越和可行性。
REFERENCES
[1] BIOT M A. Theory of propagation of elastic waves in a fluidsaturated porous solid (Part I): Low-frequency range [J]. The Journal of the Acoustical Society of America, 1956, 28(2): 168-178.
[2] BIOT M A. Theory of propagation of elastic waves in a fluid-saturated porous solid (Part II): Higher frequency range [J].The Journal of the Acoustical Society of America, 1956, 28(2):179-191.
[3] DVORKIN J, NUR A. Dynamic poroelasticity: A unified model with the squirt and the Biot mechanisms [J]. Geophysics, 1993,58(4): 524-533.
[4] DIALLO M S, APPEL E. Acoustic wave propagation in saturated porous media: reformulation of the Biot/Squirt flow theory [J]. Journal of Applied Geophysics, 2000, 44(4):313-325.
[5] LIU Y, SEN M K. A hybrid scheme for absorbing edge reflections in numerical modeling of wave propagation [J].Geophysics, 2010, 75(2): A1-A6.
[6] DAI N, VAFIDIS A, KANASEWICH E. Composite absorbing boundaries for the numerical simulation of seismic waves [J].Bulletin of the Seismological Society of America, 1994, 84(1):185-191.
[7] CLAYTON R, ENGQUIST B. Absorbing boundary conditions for acoustic and elastic wave equations [J]. Bulletin of the Seismological Society of America, 1977, 67(6): 1529-1540.
[8] ENGQUIST B, MAJDA A. Radiation boundary conditions for acoustic and elastic wave calculations [J]. Communications on Pure and Applied Mathematics, 1979, 32(3): 313-357.
[9] 夏 凡, 董良国, 马在田. 三维弹性波数值模拟中的吸收边界条件[J]. 地球物理学报, 2004, 47(1): 132-136.XIA Fan, DONG Liang-guo, MA Zai-tian. Absorbing boundary conditions in 3D elastic-wave numerical modeling [J]. Chinese Journal of Geophysics, 2004, 47(1): 132-136.
[10] 王 俊. 基于改进 BISQ模型的双相介质波场数值模拟方法研究[D]. 山东: 中国石油大学(华东), 2009: 41-45.WANG Jun. Method study of wavefield numerical simulation in two-phase medium based on the reformulated BISQ mechanism[D]. Shandong: China University of Petroleum (East China),2009: 41-45.
[11] CERJAN C, KOSLOFF D, KOSLOFF R, RESHEF M. A nonreflecting boundary condition for discrete acoustic and elastic wave equations [J]. Geophysics, 1985, 50(4): 705-708.
[12] BERENGER J P. A perfectly matched layer for the absorption of electromagnetic waves [J]. Journal of Computational Physics,1994, 114(2): 185-200.
[13] CHEW W C, LIU Q H. Perfectly matched layers for elastodynamics: a new absorbing boundary condition [J]. Journal of Computational Acoustics, 1996, 4(4): 341-359.
[14] LIU Q H, TAO J P. The perfectly matched layer for acoustic waves in absorptive media [J]. Journal of the Acoustical Society of America, 1997, 102(4): 2072-2082.
[15] ZENG Y Q, HE J Q, LIU Q H. The application of the perfectly matched layer in numerical modeling of wave propagation in poroelastic media [J]. Geophysics, 2001, 66(4): 1258-1266.
[16] COLLINO F, TSOGKA C. Application of the perfectly matched absorbing layer model to the linear elastodynamic problem in anisotropic heterogeneous media [J]. Geophysics, 2001, 66(1):294-307.
[17] 王永刚, 邢文军, 谢万学, 朱兆林. 完全匹配层吸收边界条件的研究[J]. 中国石油大学学报: 自然科学版, 2007, 31(1):19-24.WANG Yong-gang, XING Wen-jun, XIE Wan-xue, ZHU Zhao-lin. Study of absorbing boundary condition by perfectly matched layer [J]. Journal of China University of Petroleum:Edition of Natural Science, 2007, 31(1): 19-24.
[18] 赵海波, 王秀明, 王 东, 陈 浩. 完全匹配层吸收边界在孔隙介质弹性波模拟中的应用[J]. 地球物理学报, 2007, 50(2):581-591.ZHAO Hai-bo, WANG Xiu-ming, WANG Dong, CHEN Hao.Applications of the boundary absorption using a perfectly matched layer for elastic wave simulation in poroelastic media[J].Chinese Journal of Geophysics, 2007, 50(2): 581-591.
[19] 熊章强, 张大洲, 秦 臻, 周文斌. 瑞雷波数值模拟中的边界条件处理及模拟实例分析[J]. 中南大学学报:自然科学版,2008, 39(4): 824-830.XIONG Zhang-qiang, ZHANG Da-zhou, QIN Zheng, ZHOU Wen-bin. Boundary conditions and case analysis of numerical modeling of Rayleigh wave [J]. Journal of Central South University: Science and Technology, 2008, 39(4): 824-830.
[20] 李 宁. 完美匹配层理论及其在地震波场数值模拟中的应用[D]. 哈尔滨: 中国地震局工程力学研究所, 2006: 46-49.LI Ning. The theory and the application of perfectly matched layer in the seismic wave simulation[D]. Harbin: Institute of Engineering Mechanics, China Earthquake Administration, 2006:46-49.
Boundary treatment for numerical simulation of seismic waves based on reformulated BISQ model
ZHOU Zhu-sheng1,2, WANG Hong1,2
(1. Key Laboratory of Metallogenic Prediction of Nonferrous Metals, Ministry of Education,Central South University, Changsha 410083, China;2. School of Geosciences and Info-Physics, Central South University, Changsha 410083, China)
Based on first-order velocity-stress equations of the reformulated BISQ model in double-phase media, the simulation algorithm of finite difference of 2-order time and 2N-order space staggered-grid was built. Meanwhile, in order to minimum effects caused by the artificial boundary in the numerical simulation, the construction of the perfectly matched layer (PML) absorbing boundary condition and the realization of the finite-difference algorithm were discussed in detail. The arithmetic was realized with MATLAB. Compared with the conventional decaying exponential absorbing boundary and the non-absorbing boundary, the PML boundary can more effectively attenuate reflections, which is supported by the wave field modeling.
reformulated BISQ model; double-phase medium; finite-difference method; staggered-grid; perfectly matched layer (PML)
P631.4
A
1004-0609(2012)03-0976-09
国家自然科学基金资助项目(41074085,40804027);湖南省自然基金重点资助项目(09JJ3084)
2011-12-01;
2012-01-04
周竹生,教授,博士;电话:13707316924;E-mail: 672390136@qq.com
(编辑 何学锋)
