公共渔业资源下叉河捕捞的动力学模型分析
2012-01-03顾恩国廖容云范致鉴
顾恩国,廖容云,范致鉴,梁 艳
(中南民族大学 数学与统计学学院,武汉430074)
随着社会的迅速发展和人口数量的剧增,渔业资源的持续利用问题越来越引起人们的重视.对渔业资源的过度开发和捕捞严重影响了渔业资源的再生能力和持续利用[1].因此,探索渔业资源的变化规律,为资源管理者提供决策支持具有重要的意义.近年来,博弈论模型已被大量应用于描述捕捞个体之间竞争渔业资源的经济行为[2-5].对于分叉的河流,其渔业资源不仅跟经济因素即捕捞成本和捕捞利润有关,还跟环境因素即鱼类的自然生长与补充特别是鱼类在叉河的分流情况有关.现实生活中由于捕捞者的认知水平有限,他们对渔业资源在叉河的分配比例并不完全了解,或者完全不了解,因此,已有一些学者利用随机博弈论在假设渔业资源在叉河的分配比例是随机变量的前提下,建立两个独立的捕捞个体同时在各自的分叉河道进行捕捞,之后剩下的渔业资源又汇总繁殖下一代鱼的随机动态规划模型,并用计算机仿真方法分析了信息结构对渔业资源的影响[6].本文中,我们同样考虑有叉河的渔业资源,把渔业资源储量在叉河的分配比例看成系统参数的前提下建立离散动力学模型,应用博弈论的方法得到竞争至Nash均衡时的渔业资源消耗函数,然后应用非线性动力学的分析方法研究了资源再生与资源消耗的动力学模型,找到渔业资源储量在什么条件范围(可行吸引域[7])内才能保持不枯竭.
1 模型的建立
我们假设共享公共渔业资源的2个有理性个体分别在各自的分叉河道捕捞,并把捕捞到的鱼在同一个市场以:
p=a-bH,H=h1+h2,
(1)
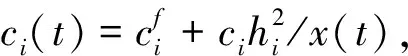
x(t+1)=x(t)(1+r-rx(t)/K).
(2)

假设渔业资源储量在叉河的分流中按比例P分配,则渔业资源在有捕捞时的演化满足:
x(t+1)=x(t)(1+r-rx(t)/K)-H(x(t))=:
F(x(t)).
(3)
这里H(x(t))是总的捕捞量,它依赖于渔业资源的储量.
假设个体1和个体2都不知道迁徙的鱼类(渔业资源)在叉河处的分配比例P的确定值,假设有Px(t)迁徙的鱼类分流到个体1所在的叉河中,那么(1-P)x(t)迁徙的鱼类分流到个体2所在的叉河中.因此,个体1和个体2的预期利润分别为:

(4)

(5)
个体1和个体2都选择自己的捕捞量,使得自身的利润最大化即maxU,要想获利润最大,需满足的条件是:
∂U1/∂h1=a-bH-bh1-2c1h1/Px=0.
(6)
∂U2/∂h2=a-bH-bh2-2c2h2/(1-P)x=0.
(7)
联立(6)和(7)式可以得到:
h1=(ab+2ac2/(1-P)x)/((2b+2c1/Px)·
(2b+2c2/(1-P)x)-b2).
(8)
h2=(ab+2ac1/Px)/((2b+2c1/Px)·
(2b+2c2/(1-P)x)-b2).
(9)
于是由(8)和(9)式可以得到捕捞总量函数为:
H(x)=h1+h2=(2ab+2ac1/Px+2ac2/
(1-P)x)/((2b+2c1)/Px)(2b+2c2/
(1-P)x)-b2).
(10)
∂H/∂x=(2ab2c1x2/P+2ab2c2x2/(1-P)+

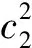
4bc2x/(1-P)+4c1c2/P(1-P))2>0.
∂2H/∂x2=(-12ab4c1x3/P-12ab4c2x3/(1-P)-

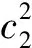

(3b2x2+4bc1x/P+4bc2x/(1-P)+4c1c2/
P(1-P))3<0.
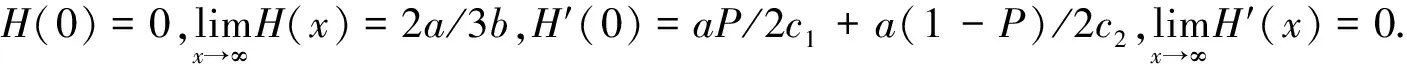
G(x)=(2ab+2ac1/Px+2ac2/(1-P)x)/
((2bx+2c1/P)(2b+2c2/(1-P)x)-b2x).
(11)
2 正平衡点的存在性
系统(3)变为:
x(t+1)=x(t)(1+r-rx(t)/K)-
(2ab+2ac1/Px+2ac2/(1-P)x)/
((2b+2c1/Px)(2b+2c2/(1-P)x)-
b2)=:F(x(t)).
(12)
系统(12)的不动点满足:
r(1-x/K)=G(x)=
(2ab+2ac1/Px+2ac2/(1-P)x)/
(x(2b+2c1/Px)(2b+2c2/(1-P)x)-b2x),
G(0)=(ac1-aPc1+aPc2)/2c1c2,

在一定的参数值下,我们可以在同一坐标系中画出G(x)和r(1-x/K)的图形,见图1.

(a) (b)

(c) (d)
由函数G(x)的性质和图1,我们可以得到下面的命题1.
命题1 设G(x)满足(11)式,则下面结论成立:
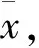


(2)如果G(0)>r,G′(0)≥-r/K那么系统(12)没有正平衡点.
(3)G(0)=r.
A .如果G′(0)<-r/K,那么系统(12)有唯一正平衡点(图1(c));
B.如果G′(0)≥-r/K,那么系统(12)没有正平衡点.
(4)假设G(0) 当不动点x*满足|F′(x*)|<1,即H′(x*)-2 aP/2c1+a(1-P)/2c2-2 aP/2c1+a(1-P)/2c2. 由于正不动点不能解析,因此我们借助于数值方法研究其稳定性和分叉性质.图2是在参数K=3,a=12,b=2,c1=1.6,c2=1.5,r∈(0.5,5),P∈(0,1)时关于自然增长率r和比例分配参数P的二维分叉图.图2中较深色和最深色区域表示参数(P,r)在该区域取值时,系统分别稳定到一周期点和二周期点.当(P,r)在白色区域取值时,系统稳定到大于20的周期轨道.此时我们认为系统稳定到准周期或混沌轨道,渔业资源出现准周期或随机波动,但不会枯竭.图3为初始渔业资源储量为x0=2.5时,得到的关于比例分配P的分叉图,其中K=3,a=12,b=2,c1=1.6,c2=1.5.当r=3(图3(a))时渔业资源稳定在一个正值(正不动点),并且最终渔业资源储量x关于分配比例P的变化为抛物线.当P=0.5时渔业资源储量处于最小值,这说明渔业资源在叉河的分配越均等,最终渔业资源储量越小,越不利于资源的保护.例如P=0.1或者P=0.9时,渔业资源储量的稳定值远远比P=0.5时大.当r=3.8(图3(b))时,渔业资源储量由稳定的二周期点(P∈(0.3,0.7))发生双向倍周期分叉,最终进入混沌状态.图4给出了渔业资源储量关于市场最高售价a的分叉图,随着a的减少,不动点经过反向倍周期分叉为混沌,其中在a=6附近出现了一个周期窗口.图5给出了渔业资源储量关于捕捞个体2的捕捞成本c2的分叉图. (a) (b) 图4 渔业资源储量x关于捕捞到的鱼在市场上的最高售价a的一维分叉图 图5 渔业资源储量x关于捕捞个体2的捕捞成本c2的一维分叉图 资源可持续利用的正平衡态的可行吸引域的形状和大小的研究对于弄清楚渔业资源的当前储量是可以维持再生能力还是最终导致该资源的枯竭起着关键作用.本节我们将利用可行吸引域的定界方法,并应用不可逆映射理论给出吸引子和吸引域的结构随参数变化所产生的全局分叉,从而揭示渔业资源储量处于什么范围才能使得资源能维持再生能力而不会枯竭,从而为资源管理决策者实施有效监控提供参考. (a)四周期吸引子及其可行吸引域 (b)混沌吸引子及其可行吸引域 在图6中,y=x与y=F(x)在第一象限的交点为正平衡点,横轴上的虚线区间表示能够再生的资源范围即可行吸引域,其边界由原点O及其一阶前像确定,横轴上的粗黑色点或者线段表示资源演化的最终正平衡态即系统吸引子.图中粗黑色线段为系统的混沌吸引子,表示渔业资源出现随机波动,我们虽然不能准确预测其最终变化,但其波动范围可由关键点和它们的像确定.横轴上的其它实线区间表示没有再生能力的也就是渔业资源最终枯竭的资源储量范围即不可行吸引域.在图6(a)的参数下,F(x)在(0,∞)内是一个单峰函数,系统有一个不稳定的正不动点x*,系统的吸引子为一个正的四周期点P1,P2,P2,P4,渔业资源出现四周期波动,其可行吸引域是由原点O及其一阶前像O-1界定的区间[O,O-1].在图6(b)的参数下,吸引子为混沌吸引子,渔业资源出现随机波动,其波动的范围仅位于区间[C1,C]内,其中C1=F(C)为C的一阶像.系统的可行吸引域是由原点O及其一阶前像O-1界定的区间[O,O-1]. 本文用博弈论的方法对有叉河捕捞的公共渔业资源建立了一维动力学模型,并运用非线性动力学方法研究了渔业资源储量在叉河处的分配比例对稳定渔业资源储量的影响,揭示了渔业资源可再生的条件和渔业资源不枯竭和储量的阈值范围. [1]Garcia M, Graiger J R. Gloom and doom? The future of a marine capture fishery[J]. Philosophical Transitions of Royal Society, 2005, B360: 21-24. [2]顾恩国,陈宝香.具有不对称对手信息的两寡头博弈公共渔业资源的动力学模型分析[J].中南民族大学学报:自然科学版,2008,27(3):96-101. [3]顾恩国,褚青涛.不同理性两个体捕捞公共渔业资源的非线性分析[J]. 中南民族大学学报:自然科学版,2009,28(2):109-115. [4]顾恩国,陈宝香.有部分个体合作的多个体博弈公共渔业资源的非线性动力学模型分析[J].中南民族大学学报:自然科学版,2008,27(1):102-107. [5] Gu Enguo. Discrete stock-effort dynamical model of a fishery on three fishing zones with a protected one [J]. International Journal of Nonlinear Sciences and Numerical Simulation, 2010, 11:137-144. [6] Mckelvey R, Golubtsov V. The effects of incomplete information in stochastic common-stock harvesting games [J]. Advances in Dynamic Games,2006, 8(5):253-292. [7] Gu Enguo. The feasible domains and their bifurcations in an extended logistic model with an external interference[J].International Journal of Bifurcation and Chaos,2007,17 (3):877-889. [8] Gordon H S. The economic theory of a common property resource: the fishery [J].Journal of Political Economy, 1954, 82:124-142.3 正平衡态的局部稳定性和分叉


4 正平衡态的全局分析

5 结语
