奇异值分解法用于MR灌注成像脑血流量估计的仿真研究

马栋敏 李 颖* 彭 川 郭延庆 郭 磊 何任杰 饶利芸5

（河北工业大学河北省电磁场与电器可靠性省部共建重点实验室，天津 300130）2（天津市第四中心医院，天津 300140）3（军械工程学院，石家庄 050003）4（University of Texas Medical School at Houston，Houston，TX77030，USA）5（The Methodist Hospital Research Institute，Houston，TX 77030，USA）

引言

MR脑灌注成像（perfusion imaging）是将组织毛细血管水平的血流灌注情况，通过磁共振成像方式显示，以评估局部的组织活力及功能（代谢能力）。它通过采用示踪剂团注技术的原始图像取得组织的信号强度-时间曲线和动脉输入函数（arterial input function，AIF），提供血液动态代谢能力信息，如脑血容量（cerebral blood volume，CBV）、脑血流量（cerebral blood flow，CBF）、平均通过时间（mean transit time，MTT）等参数［1-2］。可分析、评价组织器官的灌注状态，得到病变部位组织的微循环血流及血管变化情况等信息。

MR脑灌注成像参数的确定是一个逆问题求解的过程。Miles等提出可以用最大斜率法确定灌注参数［3］，这种方法原理最简单，但是要求示踪剂注射速率在8～10 mL/s，过高的对比剂注射速率和注射量不仅增加注射部位对比剂外渗的危险性，且要求病人有良好的心肺功能，因此这种方法在临床上并不适用。1996年，Østergaard等提出傅里叶变换和奇异值分解法都可以用来估计灌注参数［4］。研究发现傅里叶变换对噪声敏感，在信噪比低时会造成血流量的低估［5-9］，因此奇异值分解法受到人们更广泛的关注。在我国，人们对MR灌注成像的研究主要在临床应用方面，对灌注参数获取方法的研究少之又少。文中对奇异值分解法估计脑血流量进行了简单介绍，对不同阈值选择方式、信噪比、动脉输入函数的延迟和失真等因素的影响进行了仿真实验，针对奇异值分解法在动脉输入函数延迟时低估血流量的情形进行了修正，以使该方法更有效。

1 理论推导

采用示踪剂团注技术确定CBV、CBF和MTT主要基于示踪剂稀释理论。示踪剂以团注的形式从受试者静脉进入组织的过程可表示为［4］

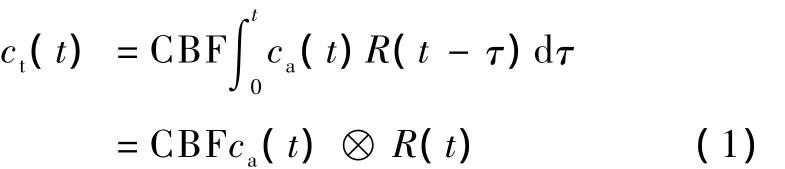
式中，⊗表示卷积运算，ct（t）表示组织示踪剂浓度，ca（t）表示动脉输入函数，R（t）表示驻留函数（residue function），即示踪剂到达组织后随着时间还留在组织内的几率，R（t=0）=1。

将式（1）离散化并写成矩阵的形式

将式（3）写为

式中，C表示最左边的矩阵，B表示最右边的矩阵，其余的用A表示。

可以从灌注所得原始图像中得到ct（t）和ca（t），为了得到 CBF，需对矩阵 A求逆，将 A进行奇异值分解，得

有

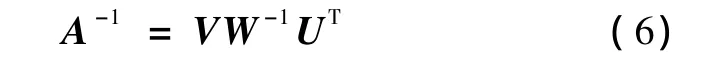
则

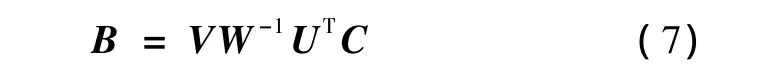
因为在灌注成像的过程中，测量噪声和生理噪声不可避免，为了降低噪声对 CBF的影响，选定阈值Psvd，将对角阵W 中小于Psvd的值给0，然后将W代入式（7）可得B。

2 仿真实验

为了验证奇异值分解法计算脑血流量的准确性，并分析其影响因素，针对不同的信噪比及动脉输入函数的延迟与失真进行了几组仿真实验。仿真试验包括以下几个方面。

2.1 模拟动脉输入函数（AIF）

所用动脉输入函数为对受试者注入标准剂量的示踪剂所能得到的经过伽马拟合的较为典型的

式中，r=3，b=5，c0=1，t0=10 s，整个曲线过程为60 s。

当脑组织发生病变时，会出现动脉输入函数的延迟或失真，这些情况都会对脑血流量的估计产生影响。在仿真实验中，通过将动脉输入函数循环平移来仿真AIF延迟；通过改变 r、b的值以改变动脉输入函数的形状来仿真AIF失真。

2.2 模拟组织示踪剂浓度-时间曲线

为了验证算法的准确性，假设已经知道驻留函数R（t），在理想的情况下，常用的驻留函数有3种描述［4］。

1）指数型（exponential）驻留函数一种函数［10］，其数学表达式为

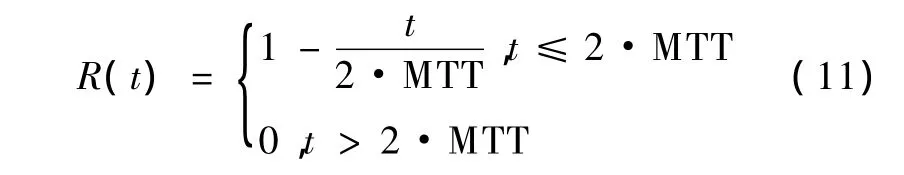
2.3 模拟信号强度-时间曲线

组织的信号强度与示踪剂浓度之间的关系为［11-12］

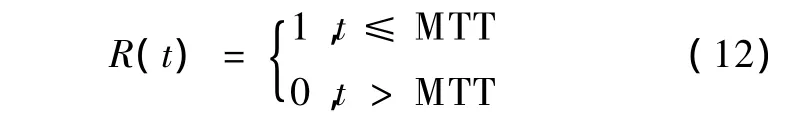
组织示踪剂浓度-时间曲线由式（1）可得，根据中心容积定理有：

3）盒型（box）驻留函数

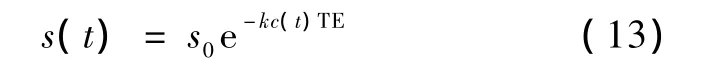
取s0=100，TE=66 ms，ct（t） 转换成st（t） 的k值是选择在 CBV=4 mL/100 mg，CBF=60 mL/100 mg/min时，信号曲线下降了原来的40％，ca（t） 转换成sa（t） 的k值是选择在 CBV=4 mL/100 mg，CBF=60 mL/100 mg/min时，信号曲线下降了原来的 60％［10］。

2.4 采用奇异值分解法作为仿真算法

考虑到生理噪声和测量噪声的影响，为了更好的模拟实际的信号强度-时间曲线，对st（t） 和sa（t）加上均值为0，标准差为σ的高斯白噪声，σ与信噪比 SNR 之间的关系［13］为

将加入噪声后的信号强度-时间曲线按式（13）变换为示踪剂浓度-时间曲线，将所得曲线采用奇异值分解法得到脑血流量估计结果。

将动脉输入函数ca（t）生成的矩阵A采用Matlab7.1中自带的奇异值分解函数进行奇异值分解得到矩阵U、V和W。奇异值分解法通过将对角阵W中小于某一阈值的奇异值置零来滤除噪声，所以阈值选择是否合适直接影响奇异值分解法对脑血流量的估计结果。

在信噪比为150和10时，对不同驻留函数不同的血流量值选择相同的阈值，在低血流量时，估计结果很好；但在高血流量时，估计结果变差。针对以上情况，提出对不同驻留函数和不同血流量值，选择不同的阈值，在高血流量时选择比低血流量时小的阈值。不同的阈值水平分别为矩阵W中最大值的15％和矩阵W中最大值的30％。

2.5 延迟效应的修正

当脑组织发生病变时，会出现动脉输入函数的延迟或失真，这些情况都会对脑血流量的估计产生影响。AIF延迟会造成高血流量的低估，所以提出对延迟效应进行修正。

修正的基本思想是：首先对示踪剂浓度-时间曲线峰值前的部分进行最小二乘拟合以得到延迟时间，然后根据此延迟时间将组织示踪剂浓度-时间曲线进行时移，最后利用时移后的曲线采用奇异值分解法得到脑血流量的估计结果。

因为噪声的影响，每次计算结果会有所不同，故在仿真实验中，每个血流量值计算200次，取均值为最终结果，且对每个血流量值200次估计结果进行了标准差的计算。标准差（sd）为

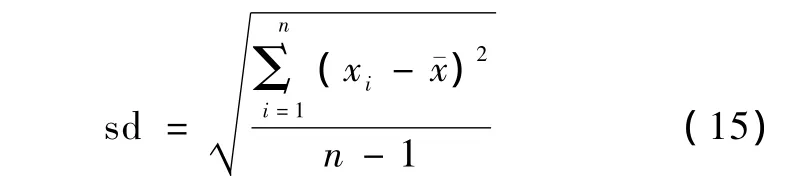
式中，xi为每次血流量估计值，¯x为均值，n为计算次数200。

3 结果

3.1 不同信噪比和阈值水平的仿真结果

图1为SNR=150，分别采用3种驻留函数，阈值分别为矩阵W中最大值的15％和30％时的结果。

由图可见，在低血流量时，阈值对脑血流量的估计结果影响不明显，估计结果很好；但在高血流量时，阈值对脑血流量的估计结果有较明显的影响，估计结果变差。这是因为在血流量值大时，其示踪剂浓度-时间曲线的峰值要大于血流量值小时的情况。显然，在不同血流量值时选择相同的阈值，会造成高血流量时有用信息的滤除或低血流量时噪声不能完全滤除。此外，由图1还可以看出，驻留函数为盒型驻留函数时，在高血流量时会有高估的情形出现。这是因为盒型驻留函数过于理想，不能很好地描述示踪剂到达组织后随着时间还留在组织内的几率。

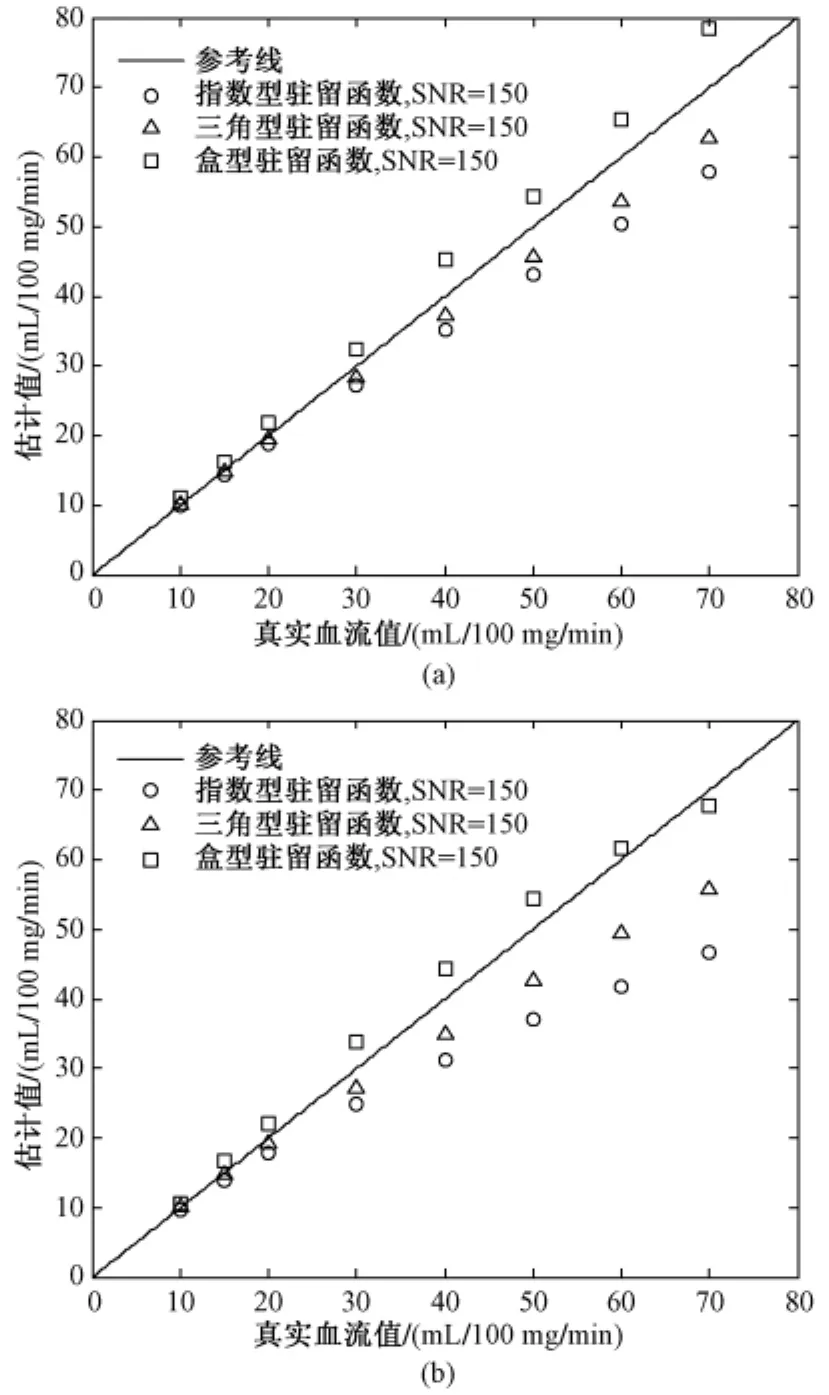
图1 SNR=150，不同阈值水平的脑血流值估计结果。（a）阈值为15％；（b）阈值为30％Fig.1 Estimated CBF values with SNR=150.（a）Psvd=15％；（b）Psvd=30％

图2为SNR=10，分别采用3种驻留函数，阈值分别为矩阵W中最大值的15％和30％时的结果。由结果可以看出，信噪比较高时，脑血流量估计较准确，且每次计算结果比较集中，此时该方法估计脑血流量结果比较稳定。当SNR较大时，阈值对脑血流量较大时的估计结果有较明显的影响；当SNR较小时，为了估计结果比较准确，需要较大的阈值来滤除噪声的影响。

3.2 不同阈值的影响

图2 SNR=10，不同阈值水平的脑血流值估计结果。（a）阈值为15％；（b）阈值为30％Fig.2 Estimated CBF values with SNR=10.（a）Psvd=15％；（b）Psvd=30％

图3和图4分别显示了SNR为150和10时，对不同驻留函数和不同血流量值，选择不同的阈值奇异值分解法对脑血流量的估计结果。对不同驻留函数不同血流量值所选阈值如表1所示。

对于图3的高信噪比情况，与图1的结果相比，可发现，在高血流量时，奇异值分解依然能够很好估计脑血流量。这说明在信噪比高时，奇异值分解法可以有效地估计脑血流量，血流量大时的标准差明显大于血流量小时。

对于图4的低信噪比情况，与图2的结果相比，可发现不管是在高血流量和低血流量时，估计结果均得到明显改善。说明信噪比小时，奇异值分解法对脑血流量的估计依然有效，但标准差随着血流量的增大而增大。

可见，无论信噪比高低，奇异值分解法都可以很好地估计脑血流量。在信噪比较高时，估计结果的标准差小于低信噪比时的标准差；信噪比相同时，低血流量时估计结果的标准差小于高血流量时的标准差。这与Østergaard L等的仿真结果相符［4］。

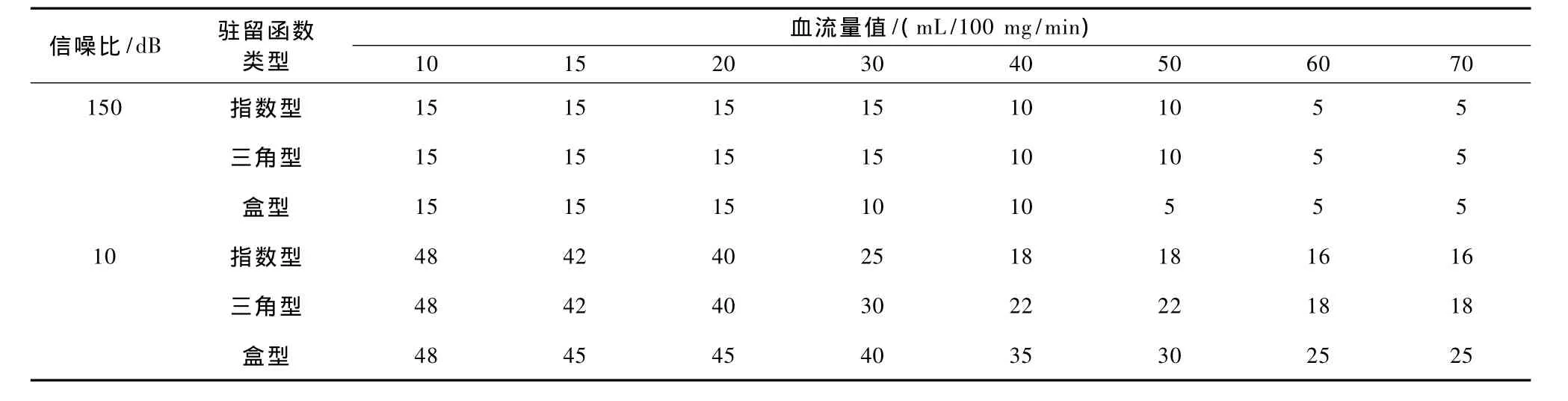
表1 对不同驻留函数不同血流量值所选阈值（％）Tab.1 The threshold for different residue function and different CBF

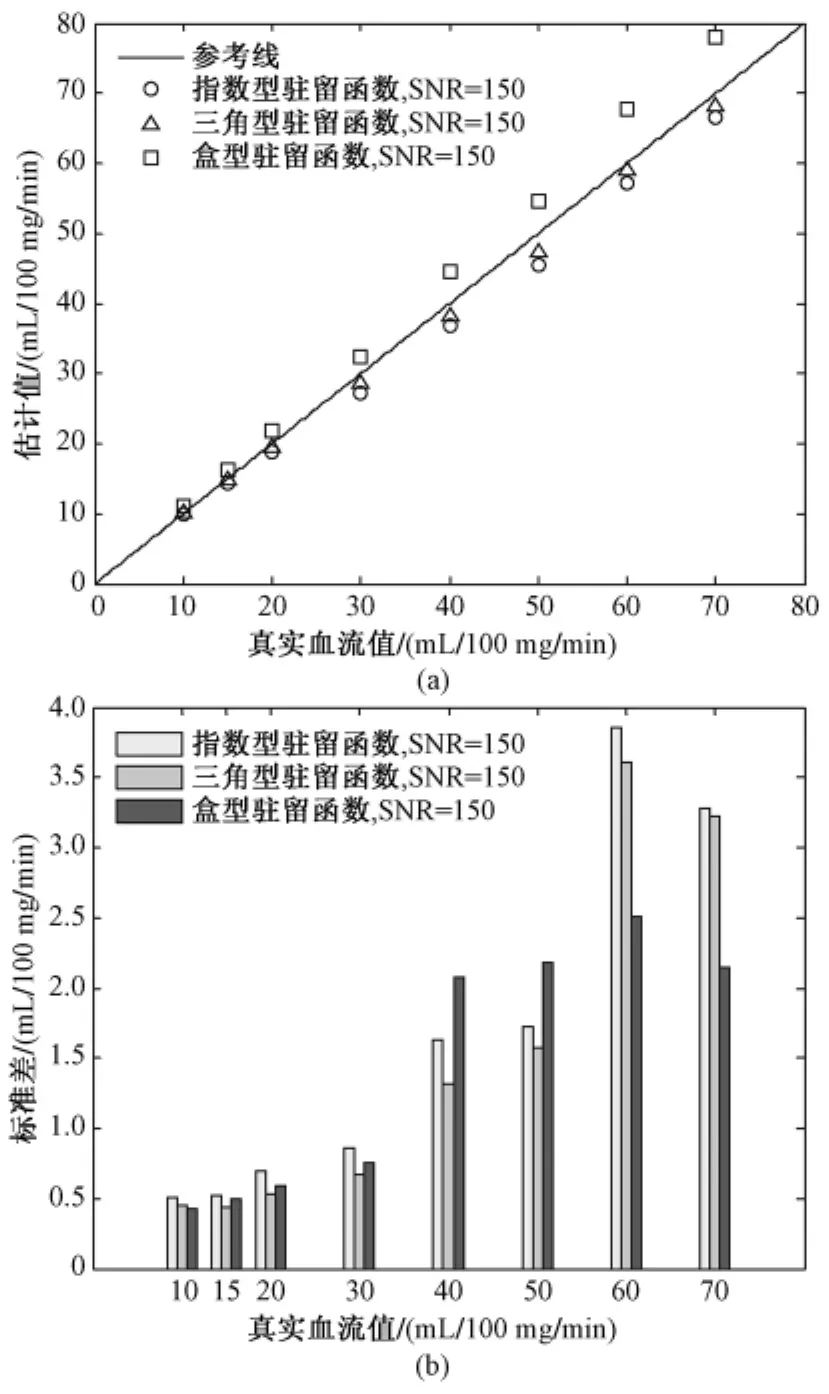
图3 SNR=150时选择不同阈值的脑血流量估计结果。（a）脑血流量估计值；（b）标准差Fig.3 Estimated CBF values with SNR=150 and differentthreshold.（a）estimated CBF values；（b）standard deviation

3.3 动脉输入函数（AIF）延迟和失真对脑血流量估计的影响

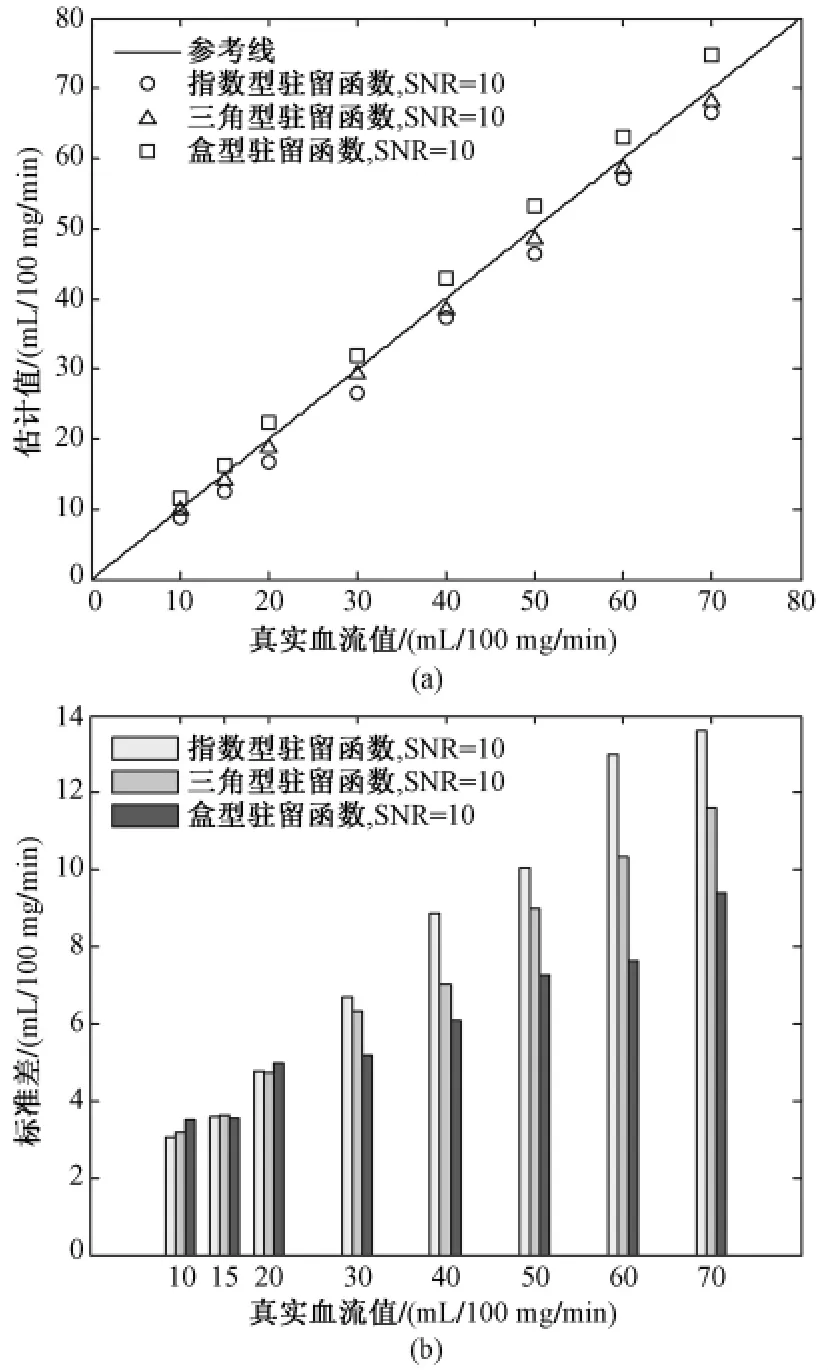
图4 SNR=10时选择不同阈值的脑血流量估计结果。（a）脑血流量估计值；（b）标准差Fig.4 Estimated CBF values with SNR=10 anddifferentthreshold.（a）estimated CBF values；（b）standard deviation

图5为AIF延迟时奇异值分解法对脑血流量的估计结果。结果显示，对于指数型和三角型驻留函数，当血流量低于30 mL/100 mg/min时，AIF延迟不会对脑血流量估计结果造成影响，当血流量高于30mL/100 mg/min时，AIF延迟会造成脑血流量的明显低估，且血流量越大，低估情形越严重；对于盒型驻留函数，低估情形不明显。这是因为盒型驻留函数过于理想，不能很好地描述示踪剂到达组织后随着时间还留在组织内的几率。

图6为AIF失真时奇异值分解法对脑血流量的估计结果。结果显示AIF失真对估计结果的影响并不明显。

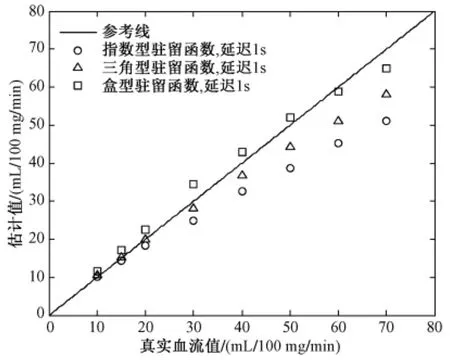
图5 AIF延迟时的估计结果Fig.5 Estimated CBF values with AIF delay

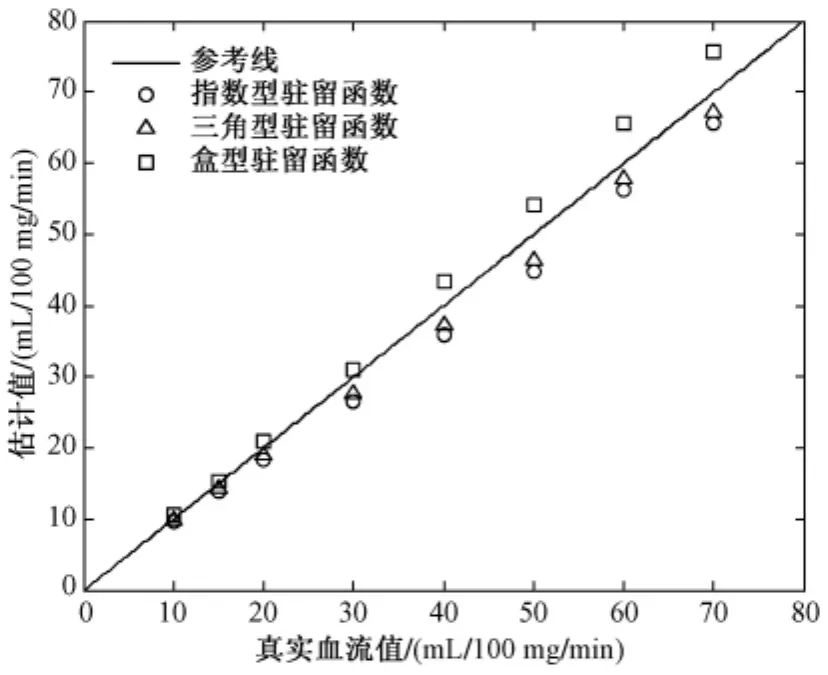
图6 AIF失真时的估计结果Fig.6 Estimated CBF values with AIF distortion

3.4 延迟效应的修正

图7为修正延迟效应前后脑血流量估计结果的比较，所用驻留函数为指数型。可以看出：延迟时间的长短对脑血流量低估程度影响不大；脑血流量越大时，低估程度越严重，当血流量为70 mL/100mg/min时，脑血流量会被低估30％左右，当血流量为40 mL/100 mg/min时，脑血流量会被低估20％左右；修正延迟效应后低估程度减小到±5％，得以改善，但是方差比修正延迟效应前明显增大，特别在延迟时间较短时。若驻留函数为三角型，修正延迟效应前后仿真实验结果与指数型驻留函数相似。

图7 修正延迟效应前后估计结果的比较。（a）CBF=70 mL/100 mg/min；（b）CBF=60 mL/100 mg/min；（c）CBF=50 mL/100 mg/min；（d）CBF=40 mL/100 mg/minFig.7 Results of simulations for comparison between delay-corrected CBF and uncorrected CBF.（a）CBF=70 mL/100 mg/min；（b）CBF=60 mL/100 mg/min；（c）CBF=50 mL/100 mg/min；（d）CBF=40 mL/100 mg/min

4 结论

本研究对奇异值分解法估计脑血流量进行了理论推导，采用了指数型、三角型和盒型三种驻留函数进行了仿真实验，分别对不同的信噪比、不同的阈值选择、动脉输入函数的延迟与失真进行了研究。

仿真实验表明，对3种不同的驻留函数，不同的血流量采用相同的阈值会造成部分血流量估计结果不准确。这是因为血流量值大时的示踪剂浓度-时间曲线的峰值较大，选择相同的阈值会造成高血流量时有用信息的滤除或低血流量时噪声不能完全滤除。对不同的血流量值采用不同的阈值可达到更好的效果。对3种驻留函数，不同的血流量采用不同的阈值，无论信噪比高低，奇异值分解法都可以有效地估计脑血流量。仿真研究表明，动脉输入函数发生失真时，该方法依然可以有效地估计脑血流量，即该方法对AIF失真不敏感。但是，该方法对动脉输入函数发生延迟比较敏感，尤其是当脑血流量较高时，该方法会造成脑血流量的低估。研究发现，低估的程度与血流量的大小有关，血流量越大低估情形越严重，而低估的程度与延迟时间的长短没有关系。经过对延迟效应影响的修正，低估情形得以明显改善，但方差有所增加，特别是在延迟时间较短时。

本研究的仿真结果表明，通过不同阈值的选择和对延迟时间的修正，奇异值分解法可对MR灌注成像脑血流量进行有效地估计，为下一步的临床数据处理打下基础，为脑部疾病的临床诊断及治疗效果的评估提供手段。

［1］Petrella JR，Provenzale JM.MR perfusion imaging of the brain：

techniques and applications ［J］.American Roentgen Ray Society，2000，175：207-219.

［2］Wong JC，Provenzale JM，Pertrella JR.Perfusion MR imaging of brain neoplasms［J］.American Roentgen Ray Society，2000，174：1147-1157

［3］俎栋林.核磁共振成像学［M］.北京：高等教育出版社，2004

［4］Østergaard L， WeisskoffRM， CheslerDA， etal.High resolution measurement of cerebral blood flow using intravascular tracer boluspassages.PartI：Mathematicalapproach and statistical analysis［J］.Magn Reson Med，1996，36（5）：715-725.

［5］Wirestam R，Andersson L，Østergaard L，et al.Assessment of regional cerebral blood flow by dynamic susceptibility contrast MRI using different deconvolution techniques［J］.Magn Reson Med，2000，43（5）：691-700.

［6］Calamante F，Gadian DG，Connelly A.Delay and dispersion effects in dynamic susceptibility contrast MRI：simulations using singular value decomposition ［J］.Magn Reson Med，2000，44（3）：466-473.

［7］Wu O，Østergaard L，Koroshetz WJ，et al.Effects of tracer arrival time on flow estimates in MR perfusion-weighted imaging［J］.Magn Reson Med，2003，50（4）：856-864.

［8］Smith MR，Lu H，Frayne R.Signal-to-noise ratio effects in quantitative cerebralperfusion using dynamic susceptibility contrast agents［J］.Magn Reson Med，2003，49（1）：122-128.

［9］Smith MR，Lu H，Trochet S，et al.Removing the effect of SVD algorithmic artifacts present in quantitative MR perfusion studies［J］.Magn Reson Med，2004，51（4）：631-634.

［10］李承锋.利用曲线拟合找到血流灌注磁振影像的血液动力参数［D］.台湾：国立阳明大学，2006.

［11］Weisskoff RM，Zuo CS，Boxerman JL，et al.Micro-scopic susceptibility variation and transverse relaxation：theory and experiment［J］.Magn Reson Med，1994，31：601-610.

［12］Fisel CR，Ackerman JL，Buxton RB，et al.MR contrast due to microscopically heterogeneous magnetic susceptibility：numerical simulations and applications to cerebral physiology ［J］.Magn Reson Med，1991，17：348-356.

［13］Unal S，Rohit S.Cerebral blood flow estimation from perfusionweighted MRI using FT-based MMSE filtering method ［J］.Magnetic Resonance Imaging，2008，26：313-322.