基于特征曲线驱动的牙齿修复体局部变形算法

闫国栋 戴 宁* 张长东 廖文和 孙玉春 王 勇 吕培军（南京航空航天大学，南京 006）

2（北京大学口腔医学院，北京 100081）

引言

随着计算机技术的发展，CAD/CAM系统开始应用到口腔修复领域［1］，取得了良好效果。目前，市场上已经推出了很多口腔CAD/CAM系统，著名的有德国Sirona公司的CEREC 3D系统、丹麦3Shape A/S公司的3SHAPE系统、德国Kavo公司的Everest系统等。在这些系统中，牙齿修复体曲面局部变形是关键技术之一，决定了修复体表面形态能否满足患者口内特定的约束条件，恢复正常的咀嚼功能。修复体CAD的局部变形应遵循以下几个基本要求：一是能够对牙尖、脊、窝等特征进行修改；二是操作灵活，且具有良好的实时性；三是修改后的修复体表面自然、光顺，避免出现皱褶或裂痕。

目前，国外商业口腔CADCAM软件中修复体曲面局部变形算法比较成熟。比如在CEREC 3D中，医生能动态编辑修复体的特征曲线，实时改变修复体牙沟区域或者边缘轮廓的形态；当变形范围较小且近似圆形时，可通过滴蜡技术，根据变形半径在局部区域产生微小的凸起或者凹下。3SHAPE系统使用的变形技术和CEREC 3D类似，也是通过特征曲线或中心控制点驱动修复体的曲面局部变形。国内关于口腔修复体数字化设计的研究起步较晚［2-4］，在修复体曲面局部变形设计方面，戴宁等提出了一种基于细分变形空间的局部变形算法。首先，构造修复体模型的细分变形空间，并将数据映射到空间中；然后，通过改变细分空间，间接改变修复体的局部形态［5］。这种算法变形不直观，而且变形范围难以确定。张翔等和李晓燕分别用B样条曲线插值修复体模型，然后通过改变B样条曲线的控制点实现局部变形。［6-7］。这种算法计算量大，难以实现实时变形。针对这一问题，本研究提出了基于特征曲线驱动的修复体曲面局部变形技术，直接在修复体曲面上选择控制点来构造特征曲线，通过编辑特征曲线来实现局部变形。实验证明，这种算法操作简便，计算效率高，可以实时进行。

1 特征曲线驱动修复体曲面局部变形

通过曲线驱动曲面变形，是由Singh等在Wires变形技术中提出的［8］。变形过程被分解为缩放、平移、旋转3个步骤，同时结合变形半径定位技术，可以实现精准的局部变形。但是，建立模型顶点和曲线映射的计算比较复杂，导致在数据较多时无法达到实时变形。在Wires变形技术的基础上，本研究优化了该算法，使之适应牙齿修复体曲面局部变形，并提出了“离散投影点算法”，可以快速地建立模型上点和曲线的映射关系。为达到更好的局部变形效果，用B样条曲线代替了Wires变形技术中使用的Bezier曲线。

1.1 曲线驱动变形原理

通过特征曲线驱动曲面局部变形，首先要在曲面上选择控制点构建特征曲线；接着是定义变形半径R，确定变形区域并建立曲线和曲面的映射关系，这一步主要是通过计算曲面顶点到曲线对应的最近点完成的。映射关系建立后，移动特征曲线的控制点修改特征曲线，即可驱动曲面顶点根据定义的密度函数F（x）移动到新的位置，从而实现曲面变形。密度函数F（x）表示变形时顶点随最近点移动的比例因子，参数x表示顶点与最近点之间的距离L和变形半径R之间的比值，定义为距离半径比，有

为保证变形边界处C1阶连续，密度函数定义为

函数如图1所示。图2表示特征曲线驱动曲面局部变形的原理：设原始曲面为S1，在上面构造特征曲线C1（见图2（a））；定义变形半径R=10并计算变形区域，pt1是S1上的一个顶点，在C1上对应的最近点为vtnear，两者距离L=6小于变形半径，则pt1在C1的变形区域内且与之对应的映射点是vtnear（见图2（b）），距离半径比是0.6；当编辑C1的控制点变形到C2，vtnear也随之移动到vt’near，驱动pt1变形到新的位置pt2。通过这种方式驱动变形区域内的所有顶点变形，从而使曲面S1变形到曲面S2（见图2（c）），具体的算法将在后面详细描述。

图1 密度函数曲线Fig.1 Density function curve

1.2 构造特征曲线

特征曲线可以有多种形式，比如Bezier曲线、均匀B样条曲线和NURBS曲线等。采用通过控制点的3次准均匀B样条曲线作为特征曲线，因为它具备良好的端点性质和局部性质，支持曲线局部编辑，便于实现修复体曲面的局部变形。生成通过控制点的3次准均匀B样条曲线，一般有两个步骤。

步骤1：先由选取的控制点求特征曲线的控制顶点［9］，有

式中，P=（p1，p2，…，pn）T为选择的控制点组成的列向量，V=（v2，v3，…，vn+1）T为待求的控制顶点列向量，M为计算矩阵（详见文献［9］）。根据准均匀B样条曲线的端点性质，有v1=p1，vn+2=pn，从而求得曲线所有的控制顶点。

步骤2：求出控制顶点后，生成B样条特征曲线，有

图2 曲线驱动变形。（a）曲面S1和特征曲线C1；（b）变形区域；（c）变形曲面S2Fig.2 The deformation illustration driven by curves.（a）surfaceS1and feature lineC1；（b）deformed region；（c）deformed surfaceS2

式中，u∈［0，1］，mi为每段B样条曲线对应的矩阵，vi为式（3）中求得的控制顶点。如果对特征曲线不满意，可通过重新拾取、添加、删除控制点的方式，重新构造特征曲线。在后续“离散投影点算法”中，使用的是特征曲线上的离散点，因此要将特征曲线均匀离散化；为提高算法精度，特征曲线离散化的采样密度一般小于0.005。

1.3 建立曲线-曲面映射关系

通过曲线驱动曲面局部变形的关键是建立两者之间的映射关系，可归纳为如下形式［10］，即

G：R3→U→R3

变形过程G由参数映射U和变形操作D两部分组成。将模型顶点pt先映射到变形空间U，完成变形后再映射回三维空间得到新的顶点pt’。也就是说，建立曲线和曲面映射，实质是建立模型顶点和曲线的映射。将上述映射关系具体化，可写为

1.3.1 生成投影曲线

因为牙齿修复体表面形态比较复杂，拾取的控制点构建的特征曲线和修复体表面并不完全贴合，会出现“穿越”或“漂浮”的现象（见图3）。如果直接建立特征曲线和模型顶点的映射，会导致变形区域不均匀，影响变形效果。因此，在建立映射之前，将特征曲线投影到修复体曲面上，生成和修复体曲面完全贴合的投影曲线（见图4）。为提高计算速度，使用基于KD树的光线追踪技术，将特征曲线上采样得到的离散点沿该点的法矢方向投影到修复体曲面上，得到投影节点，把这些节点按顺序连接起来就是投影曲线。在实际操作中，不需要将其显示出来。

图3 漂浮和穿越现象Fig.3 Floating and passing phenomenon

图4 投影曲线Fig.4 Projective lines

1.3.2 建立映射关系

建立曲线和曲面顶点的映射，常用的方法是最近投影点法［11］，即求顶点pt到特征曲线C（u）的最短距离Dis，有

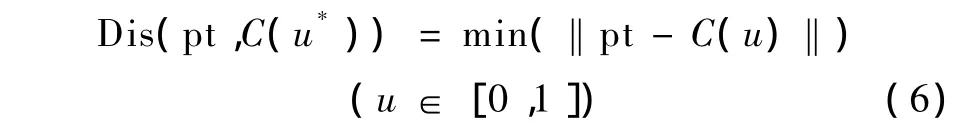
式中，u*为pt在曲线上对应的最近点参数。

如果这个问题转化为多项式根的问题进行求解，计算效率很低，数据量较大时无法在工程上达到实时应用。为突破计算瓶颈，提出“离散投影点算法”，先定义变形半径R，然后构造投影节点的KD树结构，通过KD树查找和模型顶点距离最近的投影节点，计算两者之间的距离L。若L≤R，那么模型顶点就是变形点，这样修复体模型被分成两部分，即

因为投影节点和特征曲线的离散点是一一对应的，在建立投影节点和模型顶点映射关系的同时，也建立了特征曲线离散点和模型顶点的映射关系。如果特征曲线离散点的密度足够大，则与最近投影点算法相比，“离散投影点算法”的精度损失很小，显著提高了计算效率。

1.4 局部变形

建立映射关系之后，移动控制点编辑修改特征曲线，会使特征曲线上的采样离散点发生变化，从而驱动修复体曲面局部变形。为便于表述，定义变形之前的特征曲线为Cold，记录下它的均匀离散点组Cold（vt）；定义移动控制点后新生成的特征曲线为Cnew，同时记录下它的均匀离散点组Cnew（vt）。在控制点移动后，特征曲线的均匀离散点移动向量为

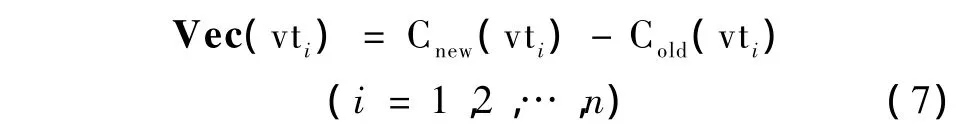
变形后新的顶点坐标为

式中，ptik是曲线离散点vti对应的变形顶点，F（x）是密度函数，xik是ptik对应的距离半径比。

2 结果与分析

开发实现平台：Windows XP系统，Visual C++.net，Hoops图形显示包。先通过前牙牙尖的局部变形说明文算法的应用及变形结果，然后在邻牙约束条件下对前牙的侧面干涉区域进行变形设计，实验结果如图5和图6所示。

2.1 前牙牙尖局部变形设计结果及分析

图5显示了前牙牙尖的局部变形设计实例。图5（a）为前牙修复体和构造的特征曲线；图5（b）、5（c）分别抬高特征曲线左边和右边的两个控制点，改变特征曲线驱动牙尖部位发生变形；图5（d）是在中间部位增加两个控制点；图5（e）将中间3个控制点向下平移，降低牙模曲面的中间区域；图5（f）在图5（e）的基础上，将中间3个控制点上移，抬高牙模曲面的中间区域。从图5中的实验结果可以看出，应用本文提出的算法，只需在牙模曲面上拾取控制点，就可以方便快捷地在修复体模型上构造特征曲线，并能在特征曲线上根据需要添加或删除控制点；通过移动特征曲线的控制点，即可驱动修复体曲面局部变形，而且修改后的曲面光顺自然，符合变形设计的要求。

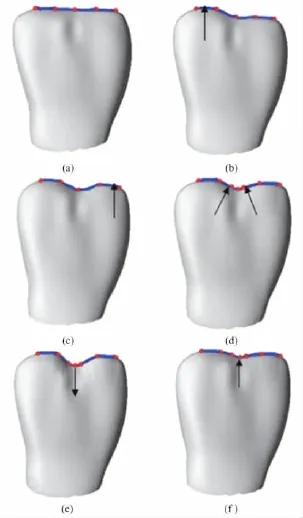
图5 前牙牙尖变形设计结果。（a）初始牙模；（b）抬高左牙尖；（c）抬高右牙尖；（d）增加控制点；（e）降低中间部位；（f）抬高中间部位Fig.5 The cusp designed result of anterior tooth.（a）initial tooth model；（b）raise left cusp；（c）raise right cusp；（d）add control points；（e）descend middle region；（f）raise middle region

2.2 前牙干涉区域变形设计结果及分析

图6是前牙修复体和邻牙发生碰撞干涉时修复体曲面在邻牙约束下变形的实例。图6（a）中箭头所指部位即是前牙修复体和邻牙的碰撞干涉区域，需要对此区域进行变形才能得到正确的修复体形态，所以要在干涉区域构造特征曲线，如图6（b）所示；为突出变形效果，将视图调整到正方向（见图6（c）），并将干涉部位局部放大，得到图6（d）的结果。图6（d）和图6（e）显示了移动特征曲线的中间控制点驱动修复体曲面变形的过程，图6（f）是最后的变形结果。从变形结果可以看出，修复体曲面在曲线驱动下形状发生改变，图6（d）中标注的干涉区域已经消失，修复体和邻牙之间的接触符合约束要求。在修复体形态设计过程中，当修复体和邻牙或对颌牙出现干涉时，都可以通过这种方法驱动修复体曲面局部变形，从而消除干涉部位。

图6 前牙干涉区域变形设计结果。（a）邻牙干涉区域；（b）构造特征曲线；（c）正面视图；（d）干涉区域局部放大；（e）移动中间控制点；（f）变形结果Fig.6 The deformation result of anterior tooth under the constraint.（a）the collision between the tooth；（b）construct the feature line；（c）front view；（d）local magnified image；（e）translate middle control point；（f）the deformed result

3 讨论和结论

在牙齿缺损或缺失之后，牙齿表面形态特征也会不可避免地丢失。现在，利用口腔CAD/CAM软件进行缺损牙齿修复，一般是从标准牙冠数据库中调用匹配的标准牙冠作为修复体。标准牙冠是统计模型数据，在各个患者的牙齿形态特征之间存在差异。要恢复患者牙齿的表面形态特征，需要用到局部变形技术。提出基于特征曲线驱动的局部变形技术，可以让用户通过计算机辅助设计，简便高效地对修复体曲面进行设计。

1）达到了牙齿修复体曲面局部变形所要遵循的基本要求，设计方法简便灵活，变形曲面光顺自然，不会出现褶皱或裂痕。

2）与文献［6-7］中曲线驱动的局部变形算法相比，不需要用B样条曲线插值拟合整个修复体曲面，只需在干涉区域构造特征曲线，避免了大量冗余计算，而且通过“离散投影点算法”快速建立特征曲线和修复体曲面的映射关系，显著提高了计算效率。

3）与商用口腔CAD/CAM软件CEREC 3D和3SHAPE相比，用户直接在修复体上选择控制点生成特征曲线的方式，以及控制点可随意增加、删除、清空的功能，提高了操作的交互性。这种方式的不利因素在于增加了用户的操作，不如CEREC 3D和3SHAPE中特征曲线内置的方式简便直接。

牙齿修复体表面形态设计是口腔CAD/CAM修复工艺中的关键环节之一，直接决定了牙齿修复的质量。只有具备强大的变形设计功能，才能设计出满足患者需求的牙齿，达到实用、高效、美观的目的。为此，提出基于特征曲线驱动的修复体局部变形方法，通过编辑特征曲线，即可实现修复体曲面的局部变形，而且变形曲面光顺自然，符合变形设计要求，这为国产口腔CAD/CAM软件核心技术的研发打下了坚实的基础。但是，还有一些问题需要解决，比如在用户自定义特征曲线的基础上，像CEREC 3D和3SHAPE一样也提供特征曲线内置的方式，这将是下一步研究的目标。

［1］Christensen GJ.Computerized restorative dentistry：state of the art［J］.Journal of the American Dental Association，2001，132（9）：1301-1303.

［2］吕培军，李彦生，王勇，等.国产口腔修复CAD-CAM系统的研究与开发［J］.中华口腔医学杂志，2002，37（5）：367-370.

［3］金树人，姚月玲，高勃，等.应用快速成型法制作磨牙树脂全冠［J］.第四军医大大学学报，2003，24（8）：700-702.

［4］韩景芸，费仁元，李彦生，等.基于逆向工程技术的后牙嵌体的数字化个性设计［J］.机械科学与技术，2005，24（3）：315-318.

［5］戴宁，周永耀，廖文和，等.口腔修复体模型曲面局部变形设计研究与实现［J］.中国生物医学工程学报，2008，27（3）：379-388.

［6］张翔，廖文和，俞青，等.口腔修复体咬合面虚拟调整［J］.中国机械工程，2006，17（20）：2130-2135.

［7］李晓燕.B样条曲线在口腔修复体局部修改中的应用［J］.上海理工大学学报，2005，27（4）：357-362.

［8］Singh K，Fiume E.Wires：A geometric deformation technique［C］.Cunningham S，Brans ford W，Cohen MF，eds SIGGRAPH’98 Proceedings of the 25th Annual Conference on Computer Graphics and Interactive Techniques.New York：ACM，1998：405-414.

［9］朱心雄.自由曲线曲面造型技术［M］.北京：科学出版社，2003.

［10］James G，Dominique B.A survey of spatial deformation from a user-centered perspective［J］.ACM Transactions on Graphics，2008，27（4）：1-21.

［11］Zhou Jinfang，Sherbrooke EC，Patrikalakis N.Computation of stationary points of distance functions［J］.Engineering with Computers，1993，9（4）：231-246.