平均血糖波动幅度计算机辅助计算算法及实现

简 峻 沈 洁 彭达明 陈 志 余学飞*（南方医科大学生物医学工程学院，广州 5055）

2（南方医科大学南方医院，广州 510515）

引言

糖尿病患者由于受到胰岛素抵抗和胰岛B细胞功能缺陷等因素的影响，致使其机体对血糖的调节能力下降，且部分糖尿病患者还存在饮食控制不佳、用药不合理及治疗的依从性较差等情况，从而使血糖总体水平偏高及血糖的波动性增大。血糖异常波动所引起的生物效应对糖尿病慢性并发症危险性的作用，远远超过血糖绝对水平的直接作用，因此对于血糖波动的监测与控制十分重要［1］。

近年来，动态血糖监测技术得到了不断的完善，已逐渐应用于临床科研和糖尿病的防治工作中。与传统的血糖监测方法相比，动态血糖监测（continuous glucose monitoring，CGM）可以提供连续、可靠的全天血糖信息，其监测结果能够更全面、准确地反映血糖波动的特征。因此，在临床研究中，以动态血糖监测数据为基础提出了多种血糖波动指标，其中最具代表性的是平均血糖波动幅度（mean amplitude of glycemic excursions，MAGE），目前被公认为是反映血糖波动的“金标准”［2］。

在实际临床应用中，平均血糖波动幅度（MAGE）值并不能直接从动态血糖监测系统（continuous glucose monitoring system，CGMS）的分析软件中得到，而是需要通过人工比较的方式筛选数据进行计算。由于动态血糖监测所得的数据量较大，当患者数据增加时，参数计算的工作量将大大的增加，这使得计算需要消耗大量的时间，从而降低了临床科研的效率。此外，为确保数据筛选的准确性，对参数进行计算分析的临床研究人员必须经过相关的专业培训，若研究人员经验不足，将导致参数的计算结果与真实值之间存在一定的误差。因此，数据的筛选受到研究人员经验的影响，使得利用人工筛选数据的准确性也相对较低。针对人工计算MAGE参数所存在的问题，笔者提出一种利用计算机自动筛选有效数据并辅助计算MAGE值的算法，从而缩短该参数计算的时间，提高参数计算的准确度和重复性，使其能够更快捷、更准确地获得动态血糖监测的MAGE参数值，提高临床科研工作的效率。

1 MAGE计算机辅助计算算法

1.1 MAGE的人工计算

平均血糖波动幅度（MAGE）参数最早由Service等在20世纪70年代提出［3］，目的是为了能够准确地反映糖尿病患者日内血糖的波动变化，但受到当时动态血糖监测技术的限制，直到近年来这一参数才逐渐得到认可。传统的人工计算MAGE有以下步骤。

步骤1：对受监测的糖尿病患者24h内的所有血糖监测数据进行统计学处理，得到血糖标准差（standard deviation of blood glucose，SDBG）。其计算公式为

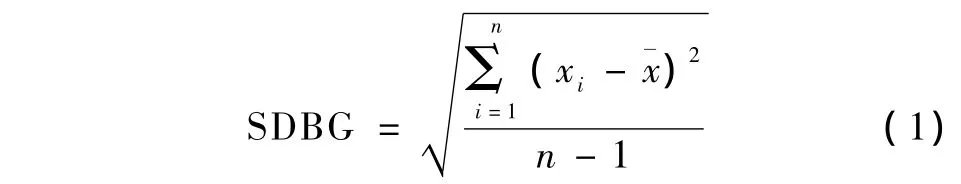
式中，n为血糖数据的个数，xi（i=1，2，…，n）为每个血糖监测数据，为所有血糖数据的平均值。

步骤2：去除所有幅度未超过一定阈值（一般为1 SDBG）的血糖波动后，根据第一个有效波动的方向（从波谷到波峰或从波峰到波谷）计算血糖波动幅度。

步骤3：统计有效血糖波动的个数（the number of effective glycemic excursions，NGE）及平均血糖波动幅度（MAGE）［4］，计算方法为

式中，AGEi（i=1…n）表示有效血糖波动幅度（amplitude of glycemic excursions，AGE），n表示有效血糖波动个数［5-7］。

MAGE最初设计的思路是采用“滤波”的方法，去除所有幅度未超过一定阈值的细小波动，从而真正反映出血糖的波动程度而不是离散特征。但由于传统人工计算存在工作量大、计算准确性受经验影响等缺点，因此在人工计算方法的基础上，提出了利用计算机自动筛选数据辅助计算MAGE算法。

1.2 MAGE计算机辅助计算算法

利用计算机辅助计算MAGE参数的关键，是让计算机正确筛选出可用于计算的数据点，即正确识别有效血糖波动。由传统人工计算MAGE方法可知，判断有效血糖波动的标准是血糖波动幅度值大于1个SDBG，这也是传统方法中唯一的判断标准，因此辅助计算算法也以此作为筛选数据的阈值，算法流程如图1所示。

图1 MAGE计算机辅助计算算法流程Fig.1 The flow chart of MAGE computer-aided calculation algorithm

为更清楚地介绍算法的实现，下面以1例从临床获得的正常孕妇24h的CGM数据（n=288）为例，说明算法的具体步骤。CGM数据如图2所示，实心圆点为进行一次24h动态血糖监测所获取到的数据点，共288个。由图2可知，临床中实际获得的动态血糖监测数据均为离散数据，且从以虚折线方式连接数据点获得的血糖数据曲线上看，动态血糖数据具有波动频率高、波动情况复杂等特点，因此导致利用传统人工方式计算MAGE参数较为复杂、工作量较大。该数据借助美国美敦力公司（Medtronic，Inc.）生产的动态血糖监测系统（CGMS Gold）获得，而系统由葡萄糖感应器、线缆、血糖记录器、信息提取器和分析软件5部分组成。在进行动态监测时，被植入脐周皮下的葡萄糖传感器与皮下组织间液中的葡萄糖发生化学反应、产生电信号，该信号通过线缆每10s被记录器记录1次，每5min系统自动将记录的电信号平均值转换成血糖值，每24h可获得288个血糖值数据。监测所得的数据以CGMS软件本身定义的数据格式存储，亦可对数据进行格式转换，使其适用于Excel等常用数据处理软件。

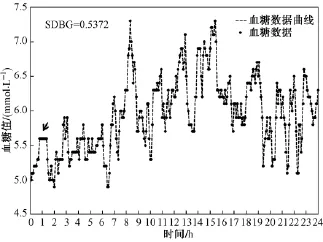
图2 CGM数据及“平台”数据Fig.2 The CGM data and the“platform”data

结合上述数据，说明算法的以下步骤。

步骤1：计算CGM数据的标准差，即SDBG，该组数据SDBG为0.537 2。

步骤2：找出CGM数据中所有的极大值数据点和极小值数据点，并记录下来。

分析CGM数据可知，在计算血糖波动幅度时，并不需要使用所有的监测数据，构成血糖波动的数据点均落在血糖波动的波峰和波谷，即曲线的极大值点和极小值点。因此，为了初步排除计算过程中不需要使用的数据点，需寻找曲线的极值点。

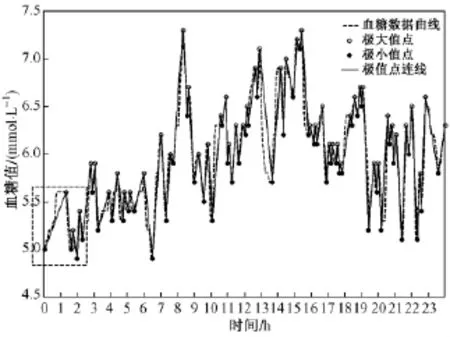
图3 CGM数据的极值点Fig.3 The extreme value points of CGM data

就连续的曲线而言，求曲线的极值点可通过求导的方式得到，但由于监测数据为离散序列，且存在连续几个数据值相等的“平台”数据（如图2中箭头所指），因此极值点不能通过求导的方式得到。算法中寻找极值点数据的过程：以微分法为基础，结合对血糖数据变化趋势的判断，找出数据的极值点位置，并对“平台”数据进行处理。以图2中的CGM数据为例，得到数据极值点的结果如图3所示。其中，空心圆点为数据的极大值点，实心圆点为数据的极小值点，虚线为以折线方式连接血糖数据点而获得的血糖数据曲线，实线为以折线方式连接所有获得的极值点数据而得到的极值点连接曲线。由图3可知，数据经过步骤2的处理，已能消除“平台”数据带来的干扰，正确地标识出所有极值点的位置，在保留极值点数据并排除非极值点数据后，即可对数据进行初步的筛选。

对于不同的受监测者，由于其自身血糖调节能力的不同，使得临床上获得的CGM数据之间存在较大的差异；此外，排除由于生理因素产生的血糖波动外，CGM数据在采集过程中还会受到多种非生理因素（如环境等）的影响，从而使数据中存在许多幅度较小的波动。综合上述原因，最终导致CGM数据波动的情况较为复杂，大大增加了利用计算机识别有效血糖波动的难度。因此，算法后续步骤的目标，是正确筛选出构成有效血糖波动的极值点数据。

步骤3：分别计算每个极大值点与其两侧极小值点的幅度差D1、D2，其中D1表示当前极大值点与其相邻左侧极小值点的幅度差，D2表示当前极大值点与其相邻右侧极小值点的幅度差。比较D1与D2绝对值的大小：如果D1绝对值大于D2绝对值，则比较D2绝对值与SDBG的大小；如果D2绝对值小于SDBG，则记录当前极大值点相邻右侧的极小值点。如果D1绝对值小于D2绝对值，则比较D1绝对值与SDBG的大小；如果D1绝对值小于SDBG，则记录当前极大值点相邻左侧的极小值点。如果D1绝对值等于D2绝对值，则比较D2绝对值与SDBG的大小；如果D2绝对值小于SDBG，则记录当前极大值点相邻右侧的极小值点。

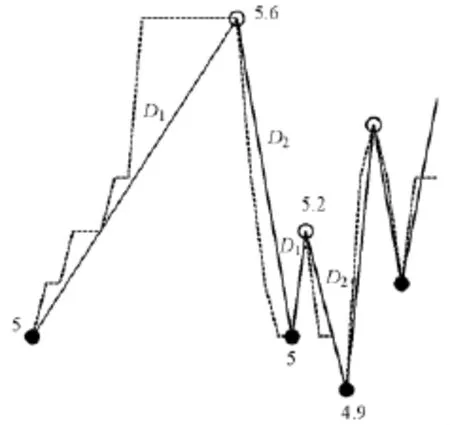
图4 数据局部放大Fig.4 The partial enlarge diagram of data

局部放大图3中的虚线框选择部分，得到部分极大值点与其相邻两侧极小值点数据，如图4所示。由图4可知，第一个极大值点为5.6，与其相邻的极小值分别为左侧5和右侧5，计算得D1=0.6，D2=0.6。此时，|D1|=|D2|，又|D2|＞SDBG，即0.6＞0.537 2，因此没有极值点被记录，继续对下一个极大值点进行操作。第二个极大值点为5.2，相邻的极小值分别为左侧5和右侧4.9，计算得D1=0.2，D2=0.3。此时，|D1|＜|D2|，又|D1|＜SDBG，即0.2＜0.537 2，因此将极大值点左侧的极小值点记录下来。剩余的极大值点依此类推。

步骤4：遍历所有极大值，把所有记录下来的数据点从极值点数据中删除，得到经过筛选后的极值点数据。

步骤5：保留相邻极小值之间最大的极大值，删除其余极大值。

步骤6：利用步骤3对筛选后的极值点数据进行处理，若依然存在需要删除标识的数据点，则转到步骤4，否则将利用步骤7计算MAGE。

由于CGM数据本身的特点，在利用②对数据进行处理后，会得到许多由小波动引入的极值点。虽然这些极值点中的一部分最后并不构成真正的有效血糖波动，但是在筛选数据的过程中不能简单地将其舍弃，因为引入这些极值点的小波动在趋势上构成了较大的波动。因此，在识别有效血糖波动时，应该将幅度值小于1 SDBG的小波动进行合并，然后重新筛选极值点数据。算法的步骤3～步骤6就是利用迭代的思想，不断将幅度较小的波动合并成大的波动，从而正确筛选出构成有效血糖波动的极值点数据。

步骤7：根据第一个有效波动的方向，计算MAGE。

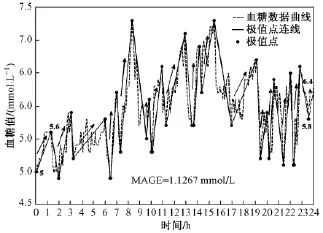
图5 筛选后获得的极值点数据及有效血糖波动计算方向Fig.5 The screened extreme value points of data andcalculation direction of effective glucose fluctuation

经过筛选，最后得到用于计算MAGE的极值点数据，如图5所示。由图5可知，实线箭头为有效血糖波动的计算方向，虚线箭头为未能构成完整血糖波动的上升沿。第一个满足波动幅度大于SDBG的波动计算方向为5-5.6=-0.6，其绝对值大于0.537 2，即计算方向为从波谷到波峰，因此在这个方向计算AGE，最后得到该CGM数据的MAGE值为1.126 7mmol·L-1。需要注意的是，虽然最后一个从波谷到波峰方向的幅度值为5.8-6.4=-0.6，其绝对值也大于0.537 2，但是最后一个上升沿后面不存在一个幅度大于SDBG的下降沿，与其构成一个完整的血糖波动，因此不是一个AGE，不能用于计算MAGE［8-11］。

2 MAGE计算机辅助计算算法软件设计

根据MAGE计算机辅助计算算法，利用Visual C#2008开发出相应的辅助计算软件。C#语言可用于创建需要运行在.NET CLR（Common Language Runtime）上的应用程序，是微软公司专门为使用.NET平台而创建的。软件主要包括以下功能模块：读入CGM数据；图形显示动态血糖监测值曲线；分析血糖数据，并显示所有波动幅度大于1SDBG的有效血糖波动；显示参数的计算结果。各功能模块及软件界面如图6（a）所示。

在读入CGM数据功能中，读入分析软件的数据存储格式以Excel软件的数据存储格式为主。因此，在利用该软件进行参数计算前，首先需利用CGMS软件将监测所得的血糖数据进行存储格式的转换，然后再将其读入分析软件中进行参数的分析。如图6（b）所示，图形显示动态血糖监测值曲线的功能采用Visual C#2008提供的MSChart控件来实现。为了能够更直观地反映出软件分析所得的有效血糖波动情况，在显示动态血糖监测值曲线的同时，还加入了将组成有效血糖波动的数据点以折线连接并以阴影填充的方式显示的功能，使得软件的使用者能够对有效血糖波动的分析结果有更具体的认识。显示参数计算结果的功能模块参考了临床科研人员的需求设计，将临床研究中需要获得的相关参数计算结果以表格形式显示，方便使用者对结果进行存储和整理，如图6（c）所示。

此外，由于对糖尿病患者进行一次动态血糖监测可获得多天的血糖监测数据，因此为了增加分析软件在使用时的灵活性、丰富分析软件能实现的功能，软件在算法的基础上，还加入了可根据实际需要对不同监测时间数据进行分析以及显示有效血糖波动起始时间与结束时间等实用的功能，如图7所示。

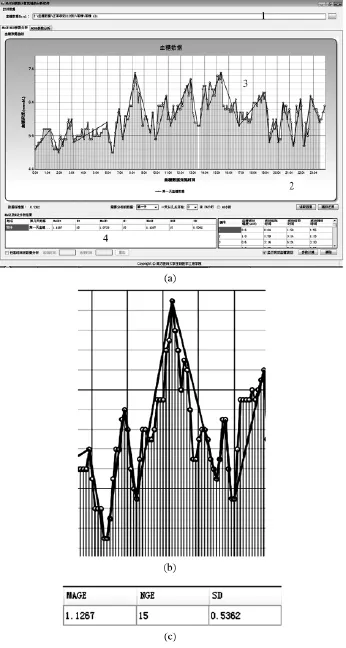
图6 MAGE参数计算机辅助分析软件。（a）软件界面及各功能模块；（b）血糖数据曲线及有效血糖波动显示方式；（c）参数计算结果显示Fig.6 The computer-aided analysis software of MAGE.（a）interface of software and the function module；（b）the view of CGM data and AGE；（c）the view of result

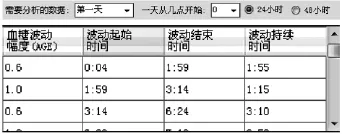
图7 分析时间选择及有效血糖波动起止时间显示功能Fig.7 The function of selecting analysistime and displaying starting and finishing time of AGE

在Pentium Dual-Core E5300 2.6 GHz、RAM 2.0GB的微机上运行MAGE辅助计算软件，利用从CGMS上导出的血糖数据进行MAGE参数的计算，计算一例数据的MAGE参数仅需花费不到1s，因此很好地解决了传统人工计算工作量大、时间花费多的缺点，大大提高了临床科研的效率。

3 实验方法及结果

为了评估MAGE计算机的辅助计算算法（MAGEc），将其计算结果与传统人工计算方法（MAGEo）的结果进行比较，比较结果以mean±SD方式表示。在采用传统人工计算方法计算MAGE参数时，参数计算结果的准确性会受到分析人员经验的影响，因此人工计算部分是由医院目前正在从事相关研究工作的研究人员来完成的，这保证了计算结果具有较高的准确性。分别利用两种方法对76例临床动态血糖监测数据进行分析计算，根据临床诊断结果，将其76例临床数据分为3组：正常成人27例（SDBG为0.895±0.345），Ⅱ型糖尿病成人患者25例（SDBG为2.108±0.695），正常孕妇24例（SDBG为0.799±0.369）。利用SPSS软件对两种不同方法的计算结果进行相关分析，并利用Bland-Altman图评估两种方法的一致性［12］，具体计算结果如表1所示。

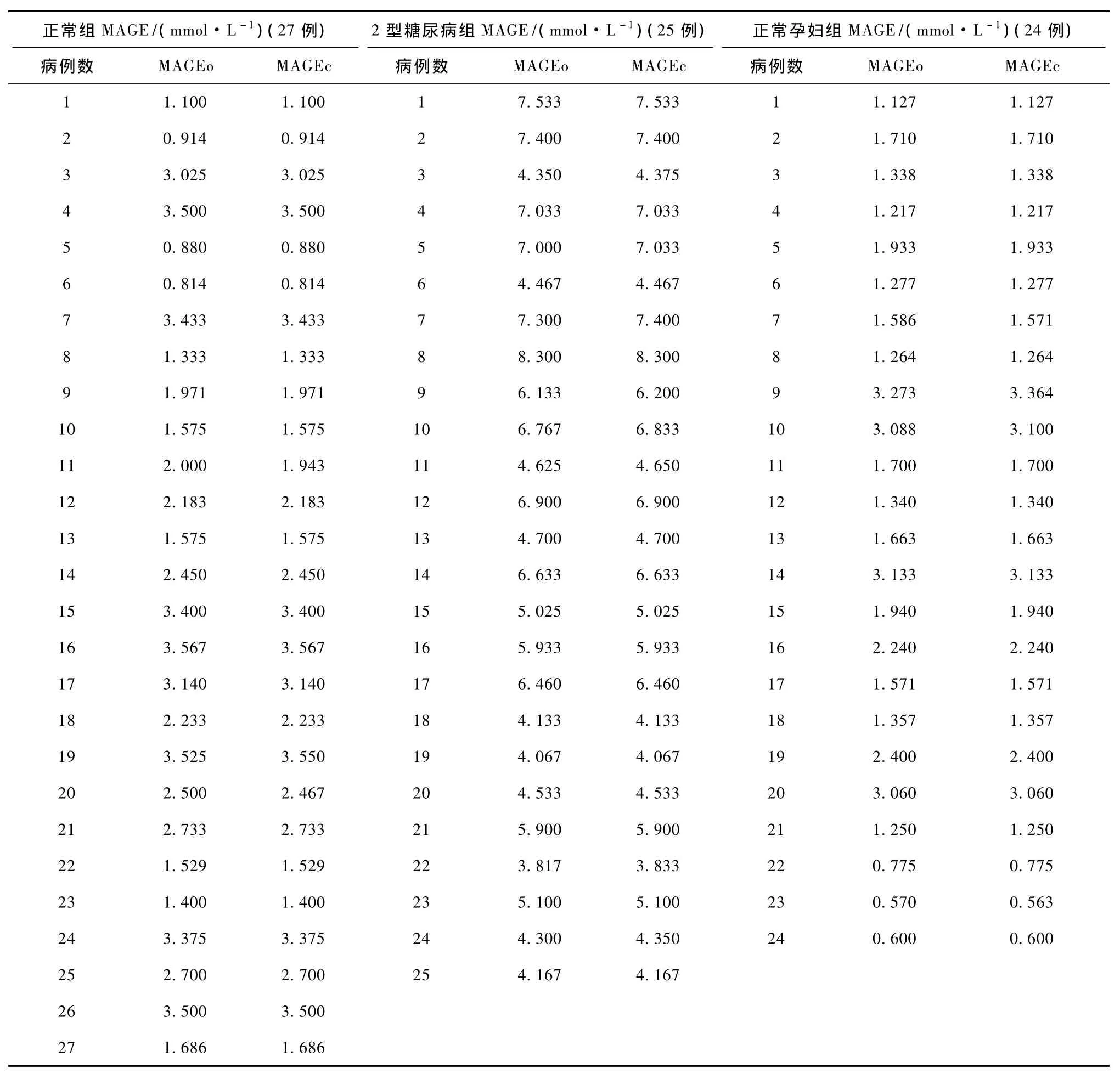
表1 MAGEo与MAGEc计算结果Tab.1 The result of MAGEo and MAGEc

3.1 相关分析

通过MAGE计算机辅助计算算法对3组数据进行计算，得到正常成人组的MAGE水平为（2.298±0.937）mmol·L-1，Ⅱ型糖尿病成人患者组的MAGE水平为（5.703±1.354）mmol·L-1，正常孕妇组的MAGE水平为（1.725±0.782）mmol·L-1。将计算结果与传统人工计算方法（MAGEo）结果进行相关分析，如图8所示。分析结果显示，MAGEc方法与MAGEo方法对于不同受监测者分组均显著相关（正常成人组r=0.994，P＜0.01；Ⅱ型糖尿病成人患者组r=0.997，P＜0.01；正常孕妇组r=0.998，P＜0.01；所有受监测者r=0.997，P＜0.01）。

图8 MAGEo方法与MAGEc方法对于不同数据分组计算结果的相关分析结果。（a）27例正常成人组；（b）25例Ⅱ型糖尿病成人患者组；（c）24例正常孕妇组；（d）76例受监测者Fig.8 The result of relevant analysis of MAGEo and MAGEc，respectively，in different groups calculating results.（a）27 normal；（b）25 with type 2 diabetes；（c）24 normal pregnant women；（d）all 76 subjects

3.2 Bland-Altman一致性分析

利用Bland-Altman图来评估两种方法的一致性，Bland-Altman图利用图形方式反映一致性界限。其中，横坐标表示用两种方法对一例数据计算结果的平均值，纵坐标表示两种方法计算结果的差值［13］，得到的Bland-Altman图如图9所示，实线表示两种方法计算结果差值的平均值，虚线表示95％一致性的上下界限。MAGEc方法和MAGEo方法对不同数据分组计算结果的差值分别为：正常成人组（-0.002 42±0.013 6）mmol·L-1，Ⅱ型糖尿病成人患者组（0.0153 3±0.027 5）mmol·L-1，正常孕妇组（0.003 4±0.019 1）mmol·L-1，所有受监测者（0.005 26±0.021 8）mmol·L-1。95％一致性界限利用mean±1.96SD公式求得，分别为正常成人组（0.024 3，-0.029 2），Ⅱ型糖尿病成人患者组（0.069 2，-0.038 6）；正常孕妇组（0.040 9，-0.034 1），所有受监测者（0.048 0，-0.037 4）。分析图8中不同的Bland-Altman图可知，落在一致性界限外的点分别为正常成人组3个，占11.1％（3/27）；Ⅱ型糖尿病成人患者组1个，占4％（1/25）；正常孕妇组1个，占4.2％（1/24）；所有受监测者6个，占7.9％（6/76）。分析结果显示，MAGE计算机辅助计算算法（MAGEc）与传统人工计算方法（MAGEo）具有较好的一致性。

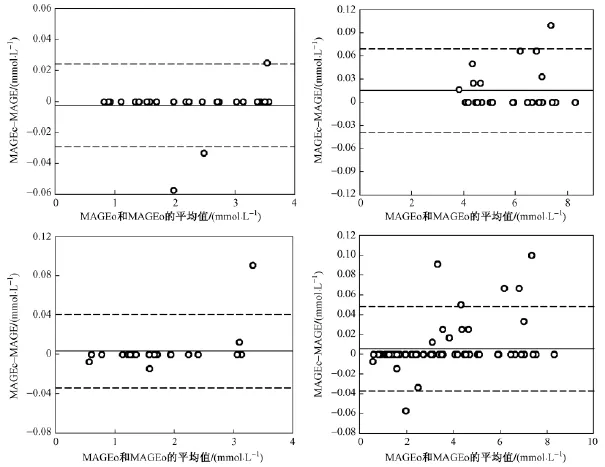
图9 MAGEo方法与MAGEc方法对于不同数据分组计算结果一致性评价Bland-Altman图。（a）27例正常成人数据；（b）25例2型糖尿病成人患者数据；（c）24例正常孕妇数据；（d）以上76例临床数据Fig.9 The Bland-Altman plot of MAGEo and MAGEc，respectively，in different groups calculating results.（a）27 normal；（b）25 with type 2 diabetes；（c）24 normal pregnant women；（d）all 76 subjects

4 讨论与结论

近年来发展的动态血糖监测作为对传统血糖监测方法的有效补充，逐渐在临床上得到推广和应用。但在临床实际应用中，作为反映血糖波动“金标准”的平均血糖波动幅度（MAGE）值并不能直接从动态血糖监测系统的分析软件中得到，而是需要通过人工方式筛选数据进行计算，这使得该参数在临床实际应用中受到了一定的限制。本研究提出MAGE计算机辅助计算算法及其软件的实现，可对大量的动态血糖监测数据进行自动筛选，并找出有效的血糖值数据，从而辅助计算出MAGE值，大大缩短了参数的计算时间，是对CGMS自带分析系统的一个有效补充。从对3个不同临床分组的动态血糖监测数据计算结果分析可知，该算法可用于计算临床中正常成人、Ⅱ型糖尿病患者以及正常孕妇动态血糖数据的MAGE值，计算所得参数结果均落在相关文献报道的范围内；而对于临床中存在的其他糖尿病患者，如儿童糖尿病患者、Ⅰ型糖尿病患者及妊娠糖尿病患者等，该算法的适用性还需结合临床实践进一步研究。在利用辅助计算软件对临床数据进行分析的过程中，除监测数据本身存在缺失会导致分析软件出错外，软件整体运行状态良好、鲁棒性较高，对于数据缺失所引起的问题可在后续的研究中有针对性地加以改进。

此外，该算法的提出对MAGE参数相关的研究具有重要的意义。在目前临床普遍采用的人工计算方法中，对于有效血糖波动的定义过于简单，其判断条件本身就存在一定的歧义，并没有对数据中出现的不同情况加以辨析说明，因此进行计算分析的研究人员必须经过相关专业的培训。若研究人员经验不足，将导致参数的计算结果与真实值之间存在一定的误差。本研究提出的算法对判断有效血糖波动的条件进行了改进和补充，解决了传统人工方法在判断有效血糖波动时存在歧义的问题，提出了一种适用于计算机自动判断有效血糖波动并自动计算MAGE参数的辅助计算算法。该算法的软件实现还简化了MAGE参数的分析过程，使得没有经过相关专业培训的人亦可以通过软件，简单而准确地计算出参数值，从而使一般糖尿病患者对自身血糖波动情况进行自我监控成为可能。而且由于软件对参数的计算速度较快，使得分析动态血糖监测者的血糖波动情况无需再待至72h（在临床中进行一次动态血糖监测，受监测者需佩戴动态血糖测量仪72h或以上）甚至更长时间后才能进行，大大提高了参数的时效性。

通过将MAGE计算机辅助计算算法所计算的结果与传统手工方法计算所得的结果进行比较分析，可知两者之间显著相关，说明两种方法之间具有较好的一致性，因此MAGE计算机辅助计算算法与传统手工方法在临床科研实践中具有较好的可替代性。利用MAGE计算机辅助计算算法，能够更快捷、更准确地获得动态血糖监测的MAGE参数值，大大提高了临床科研工作的效率。该算法及其软件的实现，已应用于对孕妇血糖波动情况进行监控，以尽早诊断妊娠糖尿病以及对Ⅱ型糖尿病患者血糖波动情况分析的相关研究中，具有广泛的临床应用前景。

［1］周健，贾伟平.血糖稳定性的意义及临床评估［J］.中华医学杂志，2006，86（30）：2154-2157.

［2］周健，贾伟平，喻明，等.动态血糖参数正常参考值的建立及临床应用［J］.中华内科杂志，2007，46（3）：189-192.

［3］Service FJ，Molnar GD，Rosevear JW，et al.Mean amplitude of glycemic excursions，a measure of diabetic instability［J］.Diabetes，1970，19（9）：644-655.

［4］中华医学会糖尿病学分会.中国动态血糖监测临床应用指南（2009年版）［J］.中华医学杂志，2009，89（48）：3388-3392.

［5］Fritzsche G，Kohnert KD，Heinke P，et al.The use of a computer program to calculate the mean amplitude of glycemic excursions［J］.Diabetes Technology＆ Therapeutics，2011，13（3）：319-325.

［6］McDonnell CM，Donath SM，Vidmar SI，et al.A novel approach to continuous glucose analysis utilizing glycemic variation［J］.Diabetes Technology ＆ Therapeutics，2005，7（2）：253-263.

［7］Monnier L，Colette C，Boegner C，et al.Continuous glucose monitoring in patients with type 2 diabetes［J］.Diabetes ＆Metabolism，2007，33：247-252.

［8］周健，喻明，贾伟平，等.应用动态血糖监测系统评估2型糖尿病患者日内及日间血糖波动幅度［J］.中华内分泌代谢杂志，2006，22（3）：286-288.

［9］Kessler L，Passemard R，Oberholzer J，et al.Reduction of blood glucose variability in type 1 diabetic patients treated by pancreatic islet transplantation［J］.Diabetes Care，2002，25（12）：2256-2262.

［10］Monnier L，Mas E，Ginet C，et al.Activation of oxidative stress by acute glucose fluctuations compared with sustained chronic hyperglycemia in patients with type 2 diabetes［J］.Journal of the American Medical Association，2006，295（14）：1681-1687.

［11］Ogata H，Tokuyama K，Nagasaka S，et al.Long-range negative correlation of glucose dynamics in humans and its breakdown in diabetes mellitus［J］.The American Journal of Physiology-Regulatory，Integrative and Comparative Physiology，2006，291（6）：1638-1643.

［12］陈卉.Bland-Altman分析在临床测量方法一致性评价中的应用［J］.中国卫生统计，2007，24（3）：308-309.

［13］张雅楠，齐玉梅，孙学丽，等.Bland-Altman法比较2型糖尿病患者能量消耗实测值与预测值［J］.实用医学杂志，2010，26（23）：4333-4335.