一种近海底质类型图生成的非参数方法

刘付程，彭俊，张瑞，董春来，张存勇

（1. 淮海工学院 测绘工程学院，江苏 连云港 222005；2. 华东师范大学 河口海岸学国家重点实验室，上海 200062）

一种近海底质类型图生成的非参数方法

刘付程1，彭俊2，张瑞1，董春来1，张存勇1

（1. 淮海工学院 测绘工程学院，江苏 连云港 222005；2. 华东师范大学 河口海岸学国家重点实验室，上海 200062）

近海底质类型图在近海工程和经济活动中有着广泛的应用价值。针对传统制图方法中存在的问题，提出了一种基于非参数指示Kriging的底质类型图生成方法。该方法能够有效地规避制图过程中的主观性，且对取样数据的平稳性和统计分布没有特殊要求，并能对制图结果的不确定性进行定量评价。该方法在连云港南部海域的应用实践表明，在相同的条件下，该方法可获得比传统方法更为精确地的制图结果，具有一定的实用价值。

沉积物类型；指示Kriging；制图

1 引 言

海洋底质类型是指依据沉积物不同粒级组分的组成情况来对沉积物进行的一种类型划分[1]。海洋底质类型图是海洋沉积调查的重要成果图件之一，它在现代海洋沉积环境分析、海洋工程建设以及浮标抛设与船舶锚泊地的选择等方面都有着广泛的实用价值[2,3]。

传统的底质类型图生成方法是根据取样点的沉积物分类结果，结合水下地形信息和专家知识而绘制的。该方法很好地利用了已知信息和专家知识，但绘制过程中主观性强，且工作效率低[2,4]。近些年来，随着计算机技术和空间分析理论的发展，基于数据驱动的底质类型图生成方法也得到了快速发展。张立华等[3]讨论了运用 Voronoi图生成技术来绘制底质类型图的方法，杨康等[4]运用距离倒数权重（IDW）和克里格（Kriging）插值方法绘制沉积物不同粒级组分的空间分布图，然后再采用栅格叠合技术制作底质类型图。尽管这些方法在很大程度上规避了制图过程的主观性，但在实际应用过程中仍然还存在不同程度的局限性，如Voronoi图法和 IDW 法对沉积物粒度空间分布的自相关性没有给予足够的重视，而 Kriging法则要求空间现象具备二阶平稳或服从某种统计分布假设，这些都对制图结果的可信度和方法的适用范围产生不利影响。此外，目前大多数成图方法都未能给出制图结果不确定性的定量评价信息，这也在一定程度上制约了成果图的有效应用。本文以连云港南部海域为例，尝试运用非参数地质统计学中的指示克立格（Indicator Kriging）方法来对近海沉积物类型进行制图，并对方法的适用性和制图结果精确性作出评价。

2 非参数法制图的基本原理

2.1 基本思想

对于研究海域的M个表层沉积物样本，可依据一定的沉积物分类和命名方法（如Shepard分类法)将其划分为N种类型。若这N种沉积物在该海域的某一个非取样点处发生或出现的概率分别为P1、P2、…、PN，则存在如下的一个合理推断：当P取最大值时，它所对应的沉积物类型即为该非取样点处的沉积物类型。基于这一推断，制图的关键就转变为如何估计不同类型沉积物在所有非取样点处发生的概率，然后再通过比较概率值的大小来确定非取样点处的沉积物类型，从而实现制图。

若将沉积物取样看成是对指定类型沉积物空间分布概率的一次实现，则相对于指定类型的沉积物而言，所有采样点的概率值要么是 1（即该采样点为指定类型沉积物），要么是0（即该采样点为其它类型沉积物），据此可以采用非参数地质统计学中的指示 Kriging方法来估计指定类型沉积物在所有非取样点处出现的概率。

2.2 指示克立格（Indicator Kriging）

指示克立格是条件普通Kriging的非参数形式，最早由Journel提出[5]。该方法可对非取样点处的条件概率分布函数（Conditional Cumulative Distribu--tion Function, CCDF）进行估计，且该方法不依赖空间现象的平稳性，也不要求区域化变量服从某种分布假设，因此该方法在很多领域得到了广泛地应用[6,7]。限于篇幅，本文只结合不同类型沉积物空间分布概率的估算来对其原理作一简要的介绍，更详细的内容，读者可以参考文献[5,8]。

假设在某海域进行沉积物取样，经实验室分析后获得各样品不同粒级组分的质量分数。若Z为基于指定分类方法（如Shepard分类法）的某一类型沉积物不同粒级组分的组合条件(即砂、粉砂和粘土的质量分数)，则在位置x处可定义如下的阶梯函数(即指示函数)：

式中z(x)为位置x处的沉积物粒度组成情况。z(x)∈Z表示位置x处的粒度组成符合指定类型沉积物的粒度组成要求。在给定的Z条件下，z(x)∈Z时(即I(x,z)=1)的概率为

则指示函数I(x，Z)的期望值为

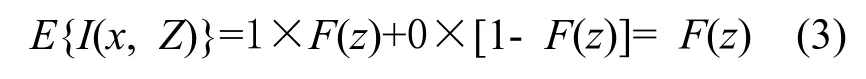
上式表明，位置x处的沉积物为指定类型沉积物的概率等于指示变量的平均值。当I(x+h, Z)和I(x, Z)为被矢量h（又称步长）分割的两个位置x+h和x处的指示函数值时，则指示变异函数γI(h, Z)可定义为

根据(4)式可求得指示变异函数相对于步长h的散点图，该散点图可用球状、指数、高斯等理论模型来拟合，从而可以求得指示变异函数的拟合理论模型。据此可进一步采用普通Kriging方法来估计未知点 x处的 I(x,Z)值，也即指定类型沉积物在点 x处出现的概率，即

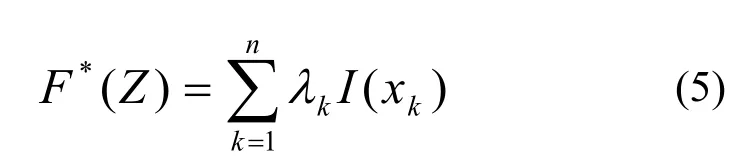
式中F*(Z)为满足粒度组成条件Z的指定类型沉积物，在待估点x处的概率F的Kriging估计；n是待估点x邻域中的样点数；xk是邻域中的第k个样点的位置；λk是第k个样点的权系数，它是在满足最优无偏估计条件下，由指示变异函数来确定[5,8]。

3 试验与分析

3.1 试验数据

试验区域为连云港港口以南、灌河口以北、低潮线和大约-12 m等深线之间的海域。2005年9月在该海域采集了106个表层沉积物样品，样点位置以GPS定位，采用垂直岸线的非网格化样点布设方式，样点分布见图 1。沉积物样品经实验室分析获得相应的粒度组成数据，再依据Shepard分类法对其进行类型划分和命名[1]。为便于对制图结果进行评价，所有样本数据被随机地分成2组，一组为插值数据集，用于制图过程，共有 96个样本数据；另一组为验证数据集，用于检验制图结果准确性，共有10个数据，其空间分布见图1。

图 1 采样点分布图及沉积物分类结果Fig. 1 Sampling sites and their sediment types based on Shepard textural classification system

3.2 结果与分析

3.2.1 不同类型沉积物指示变异函数的计算根据Shepard分类法，研究海域所有样本数据可划分为砂、粉砂质砂、砂-粉砂-粘土、粉砂、砂质粉砂和粘土质粉砂等6种类型沉积物（图1）。据此可分别按照6种类型沉积物的粒度组成要求，对所有样本进行指示变换，得到相应的指示变量值1和0，在此基础上运用地统计学软件 GS+7.0分别计算 6种类型沉积物的指示变异函数值，再经理论模型拟合后得到相应的理论模型模型参数（图2）。

图 2 不同类型沉积物的指示变异函数及其拟合模型和参数Fig. 2 Semi-variance of different types of sediment and their fitted models and parameters

从图2可以看出，6种类型沉积物的指示变异函数均可以用球状模型进行拟合，表明其空间变异均存在明显的结构性特征。因此可以进一步利用Kriging方法对6种类型沉积物的指使变量（即出现概率）进行空间估计。

3.2.2 不同类型沉积物空间分布的条件概率估计图3是基于图2给出的不同类型沉积物指示变异函数的拟合理论模型，经GS+7.0中的Krigng插值方法得到的不同类型沉积物空间分布的条件概率图。从图3可以看出，不同类型沉积物空间分布的条件概率存在明显的空间互补性，也即它们条件概率高值的分布在空间上是相互错位的，这表明不同类型沉积物分别占住了研究海域的不同空间位置，这显然对制图是十分有利的。

图3 不同类型沉积物空间分布的条件概率分布图Fig. 3 Conditional probability distribution map of different types of sediments

3.2.3 底质类型图的生成及其不确定性评价依据不同类型沉积物空间分布的条件概率图，可采用硬化的方法获得研究海域的底质类型图。硬化是指将每一位置最大概率值所代表的沉积物类型作为该位置的沉积物类型。该过程可通过地理信息系统软件ArcGIS9.2中的地图代数运算功能来实现。图4即硬化后的研究海域底质类型图，该图清楚地给出了研究海域不同类型沉积物的空间分布情况。

图 4 连云港南部海域底质类型图Fig. 4 Map for sediment types in Lianyungang southern sea area

由于硬化过程在接受一种类型沉积物的同时，也忽略了其它沉积物在该点发生的可能性，因此硬化过程产生一种忽略不确定性。忽略不确定性是与该位置沉积物类型的过渡性相关，当不同类型的沉积物在某点出现的概率越接近时，其忽略不确定性也就越大，制图结果的可靠性也就越低，因此计算每点的忽略不确定性可生成相应的不确定性图，该图可以用于评价制图结果的可靠性。忽略不确定性可以通过熵来表征[9]，熵表达了沉积物出现概率集中趋向某一特定类型沉积物的程度。熵的计算公式如下：

式中，Pikj是第k种沉积物在栅格单元(i, j)处出现的概率；l是研究海域已知的沉积物类型，本文中 l为6，Hij是点(i, j)处的熵，其取值范围从0到1。当Hij为0时，表示点(i, j)处的沉积物完全属于某个类型，在硬化过程中不会产生对其它类型的忽略。当Hij为1时，表示不同类型沉积物在该点处出现的概率相同，即没有一种类型沉积物可以较好地代表该点的沉积物，因此该点划分为任何一种类型的沉积物都会产生最大的忽略不确定性。根据式(6)，运用ArcGIS9.2的栅格运算功能可获得研究海域的熵分布图（图5），也即忽略不确定性大小分布图。

图 5 底质类型图的忽略不确定性Fig. 5 Ignored uncertainty of the sediment type map

从图5可以看出，研究海域忽略不确定性在研究区的东南部和西北部相对较小，表明该海域制图结果的可靠性高；而忽略不确定性在中部呈现斑块状高值分布，说明该斑块区制图结果的可靠性相对较低。结合图1可以发现，忽略不确定性的高值分布区主要分布在具有多种类型沉积物的交界区，而低值区则主要分布在同一种类型沉积物的集中连片分布区域。这现象符合一般的推理结论，表明不确定性图可以用于评价底质类型图的可靠性。

3.2.4 制图结果的精确性评价 为比较和评价制图结果的精确性，表1给出了验证数据集中所有样点处沉积物类型的实测结果和制图结果，表1同时还给出了按照文献[3]和[4]中方法的制图结果。

从表1可以看出，本文所提出的非参数方法只有5号样点与实测结果不一致，其它9个样点的制图结果都与实测结果相同；而IDW和Kriging方法的制图结果均有4个样点（2、3、4、5号样点）与实测结果不一致，表明非参数方法在制图结果的精确性方面要好于IDW和Kriging方法。尽管Voronoi图法的制图结果也只有1号样点与实测结果不一致（表1），但该方法对样点的位置分布十分敏感，任何一个样点位置的微小偏移都会造成制图结果的显著变化，因此该方法的稳健性不够好；相反，非参数方法是基于指示变量空间变异的结构性特征来进行空间估计，它对位置敏感性相对较低，因此其适用性要较Voronoi图法更为宽泛。

表 1 沉积物类型的制图结果与真实结果的比较Tab. 1 Comparison between the mapping types and actual types of sediment

4 结 语

基于指示 Kriging的近海底质类型图生成的非参数方法，能够有效地规避制图过程中的主观性，且对沉积物取样数据的平稳性和统计分布没有特殊要求，并能对制图结果的不确定性进行定量评价。该方法在连云港南部海域底质类型制图的应用实践表明，在相同的条件下，它可获得比传统方法更为精确地制图结果，具有较强的适用性和应用价值。

需要指出的是，沉积物类型的空间分布受水下地形地貌的影响显著，在本文的非参数成图方法体系中，地形地貌因素未被考虑，因此该方法在水下地形变化较为复杂海域的应用效果还需要进一步检验。如何将沉积物类型的空间分布与水下地形地貌及水动力环境变化之间的关系纳入到非参数成图方法体系中，是值得进一步探讨的问题。

[1] 国家海洋局908专项办公室编. 海洋底质调查技术规范 [M]. 北京: 海洋出版社, 2006: 33.

[2] 刘锡清. 最新中国近海陆架底质类型图 [J]. 海洋地质与第四纪地质. 1992, 12(4): 11-20.

[3] 张立华, 崔高嵩, 张建军, 等. 一种海底底质与地形的信息叠置可视化方法及应用 [J]. 测绘科学, 2007, 32(4):111-112, 115.

[4] 杨康, 张永战. 基于栅格叠合的沉积物底质图生成方法 [J]. 第四纪研究, 2007, 27(5): 889-895.

[5] Journel A G. Non-parametric estimation of spatial distribution [J].Mathematical Geology, 1983, 15(3): 445-468.

[6] 刘瑞民, 王学军, 张巍. 天津表土 PAHs区域环境风险评价研究[J]. 环境科学, 2008, 29(6): 1719-1723.

[7] 徐英, 陈亚新, 王俊生, 等. 农田土壤水分和盐分空间分布的指示克立格分析评价 [J]. 水科学进展, 2006, 17(4): 477-482.

[8] 侯景儒. 指示克立格法的理论及方法 [J]. 地质与勘探, 1990, 26(3): 28-38.

[9] Zhu A X. Measuring uncertainty in class assignment for natural resource maps under a similarity model [J]. Photogrammetric Engineering & Remote Sensing, 1997,63:1195-1202.

A non-parametric method to generate type and distribution of coastal surface sediment map based on indicator kriging

LIU Fu-cheng1, PENG Jun2, ZHANG Rui1, DONG Chun-lai1, ZHANG Cun-yong1

(1. School of Geodesy and Geomatics Engineering, Huaihai Institute of Technology, Lianyungang 222005, China;
2. State Key Lab of Estuarine and Coastal Research, East China Normal University, Shanghai 200062, China)

Coastal surface sediment type map has been widely used in marine economic and engineering activities, but the traditional mapping methods had some shortcomings due to their intrinsic assumption. In this paper, a non-parametric method of indicator kriging has been proposed for generating types and distribution of coastal surface sediment. The method can effectively avoid mapping subjectivity, and has no special requirements for the sample data to meet second-order stationary or normal distribution, and can also provide useful information on the quantitative evaluation of mapping uncertainty. The application of the method in the southern sea area of Lianyungang showed that much more mapping precision could be obtained compared with the traditional methods such as IDW, kriging and Voronoi under the same condition, so the method had some promotion and practical values.

type of sediment; indicator kriging; mapping

P736.21

A

1001-6932(2011)05-0551-06

2010-12-03；

2011-04-26

江苏省高校自然科学基金项目（07KJD170012）；江苏省测绘科研项目(JSCHKY201005)；淮海工学院自然科学基金项目(Z2008009)。

刘付程（1971—），男，安徽安庆人，副教授，博士，主要从事海岸带环境演变和GIS应用研究。电子邮箱：iliufucheng@126.com。