一个改进的二阶Boussinesq方程模型在线性波浪反射问题中的适用性研究

蒲高军，刘忠波，康海贵

（1. 大连理工大学，辽宁 大连 116024；2. 大连海事大学， 辽宁 大连 116024）3. 胜利油田胜利勘察设计研究院有限公司，山东 东营 257026）

一个改进的二阶Boussinesq方程模型在线性波浪反射问题中的适用性研究

蒲高军1,3，刘忠波1,2，康海贵1

（1. 大连理工大学，辽宁 大连 116024；2. 大连海事大学， 辽宁 大连 116024）3. 胜利油田胜利勘察设计研究院有限公司，山东 东营 257026）

基于改进型的二阶Boussinesq方程，在交错网络下建立数值模型。利用模型模拟波浪在常水深情况下的传播，波浪反射系数均低于2%。利用该模型模拟波浪在平斜坡前的反射，并将数值结果与解析解进行对比。结果表明，对于相对水深较大情况，坡度较陡时模拟结果明显偏大；对于相对水深较小情况，坡度超过1∶ 1时，数值结果仍与解析解有较好的吻合。最后将模型分别应用到有限个连续沙坝上Bragg反射问题和弧型地形上的波浪反射问题中，并将数值结果与相应的实验结果进行了比较。前者对比表明，整体数值结果与实验结果吻合较好，但在双沙坝问题上共振点处反射系数明显偏大；后者对比表明，当弧型地形切角角度小于 40°，数值结果与解析解吻合较好。

Boussinesq方程；波浪；反射

1 引 言

改进型的二阶Boussinesq水波方程是能综合考虑波浪折射、绕射、浅水等综合性能，被广泛的用来求解各类波浪问题：如潜堤上或沙坝上的波浪传播变形以及三维复杂地形上的波浪折射绕射等问题[1-3]，因此它是一种高效的时域计算数学模型。但是二阶Boussinesq水波方程在线性波浪反射问题上的适用性如何，目前相关的研究不多。同时在解决这个问题前，须考虑到所建立的Boussinesq数值波浪水槽在平底情况下边界条件的反射程度，只有建立的模型在平底条件下的反射系数小，才能利用它们求解其他线性波浪反射问题。因此本文将选择笔者给出的改进型 Boussinesq水波方程作为研究对象[4]，先建立低反射性能的波浪水槽，进而利用该模型模拟在平斜坡、沙坝地形以及弧型地形上的波浪传播变形，通过二点法求出在这些复杂地形上的线性波浪反射系数，并将这些系数与相关解析解、实验结果进行了比较，综合考察了该方程在线性波浪反射问题上的适用性。

2 改进型Boussinesq方程及模型

2.1 基本方程

刘忠波等推导了改进型的 Boussinesq水波方程[4]，其表达形式为：

2.2 数值模型

在方程(1)和(2)的基础上，笔者分别基于交错网格和非交错网格体系下，建立了不同的有限差分数值计算模型，在交错网格下采用Crank-Nicolson格式进行求解方程，在非交错网格下采用混合四阶Adams-Bashforth-Moulton格式进行求解方程。综合考虑到交错网格下数值计算更稳定的特点以及四阶Adams-Bashforth-Moulton格式的高精度特点，建立了数值模型。模型中的变量的一阶导数采用4阶精度，二阶导数采用2阶精度，需要注意的是由于交错网格的存在，当连续方程和动量方程出现同样项时采用的格式是不一样的。在一维模型中引入内部造波源项（单点源项），并且在两边界 2倍波长范围内设置海绵边界层进行消波处理。

3 数值模型的应用

3.1 常水深情况下的数值水槽反射

将数值模型应用到平斜坡等地形上波浪反射情况计算前，先进行了常水深情况下波浪水槽的反射系数情况对比（计算结果见图1）。图1中给出了不同无因次水深下的波浪反射系数，其中反射系数值均低于2%，且h/L处于区间[0.1，0.38]时，系数值低于0.5%，这说明该模型可用于求解其他情况的波浪反射问题。

图 1 常水深情况下的波浪反射系数Fig. 1 Numerical wave reflection coefficient in a constant wave flume

3.2 平斜坡上的波浪反射

这里考虑的地形是两个平水深0.6 m和0.2 m，两个不同水深间是一个平斜坡，坡度变化有 4∶1到1∶25。Suh等[5]给出了有限元模型的线性数值结果作为考察本文模型在这一问题适用性的比较对象。图2－图6给出了波浪周期为1.0～5.0 s的数值波浪反射系数，图中b代表斜坡的水平长度。当波浪周期不同时，反射系数与b之间存在明显的周期变化特点，这种周期的震荡幅值随着坡度的减缓而变小；在给定的坡度变化范围内，周期越大，反射系数的周期变化个数越少，反之越多。由图2和图3可知，对于相对水深较大的小周期波浪，当坡度较陡时，该方程模拟结果明显偏大，与有限元解吻合程度差，该方程只适用于坡度较小的情况，图 2给出最大适应坡度约为1∶2.5，而图3给出的坡度是1∶1。对于相对水深较小的长周期波浪（见图4－图6），当波浪周期等于2 s时，且坡度等于4∶3时，数值结果仍与有限元数值解有较好的吻合；而当波浪等于5 s时，数值解在坡度4∶1的情况下，与有限元数值解的吻合也很好，这说明本文方程更适合于长波问题的求解。此外，图4也给出了利用邹志利[6]模型计算的结果，二者在色散性和变浅作用是一致的，它们存在的差异主要源自于邹的方程中含有(hx)2项和不同的hxx项，而在这一地形上的hxx=0。因此这是(hx)2项的引入导致利用该模型计算的结果比有限元数值解更偏大的主要原因。结合图2－图6，我们也可得到下面结论：当给定坡度时，随着周期的变化，反射系数也存在周期性的震荡。

图 2 平斜坡上的波浪反射系数（1.0 s）Fig. 2 Wave reflection coefficient of a plane slope （1.0 s）

图 3 平斜坡上的波浪反射系数（1.33s）Fig. 3 Wave reflection coefficient of a plane slope （1.33s）

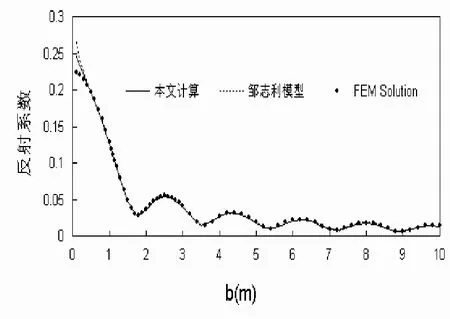
图 4 平斜坡上的波浪反射系数（2.0s）Fig. 4 Wave reflection coefficient of a plane slope （2.0s）

图 5 平斜坡上的波浪反射系数（2.86s）Fig. 5 Wave reflection coefficient of a plane slope （2.86s）

图 6 平斜坡上的波浪反射系数（5s）Fig. 6 Wave reflection coefficient of a plane slope （5.0s）

3.3 有限沙坝上的波浪反射

Davies和 Heathershaw[7]和 Guazzeli等[8]分别进行了沙坝上Bragg反射的实验。前者实验中分别采用了2个、4个和10个沙坝，每个沙坝长为1 m，沙坝波幅为5 cm；2个沙坝和4个沙坝存在时的平底水深为0.156 m，10个沙坝存在时的平底水深为0.313 m；后者采用的沙坝为双正弦型。

为了简便起见，给出了两组数值计算结果，见图7和图8。 图7也给出了利用邹志利模型的数值计算结果，由图7可以看出，尽管缺少（hx）2项，本文数值结果与实验吻合程度很好，同时与邹[6]的模型计算相比，二者计算结果相差不大，仅当波长等于沙坝长度时，二者存在一定的差异，且邹的模型计算结果偏大，该差异源自后者模型中含有（hx）2项和不同的hxx项。由图8可以看出，虽然共振的位置时模拟的与实验结果一致，但计算值比实验值偏大。

图 7 数值计算结果与Davies和Heathershaw[7]实验结果的比较Fig. 7 Comparisons of the simulated results with experimental results for sine topography

图 8 双正弦地形上计算结果与Guazzeli等[8]实验结果的比较Fig. 8 Comparisons of the simulated results with experimental results for two-sine topography

3.4 弧型地形上的波浪反射

Lee等[9]给出了弧型地形上的数值解结果，本文利用该数值结果检验了本文方程的适用性，对比结果见图 9。由图可见当弧型地形切角角度超过40°，数值结果与边界元数值解存在明显 的差别，而实际中海岸沙坝的迎浪面能维持住的相对稳定坡度一般低于该值，这说明就线性波浪反射问题，该方程仍然是可用的。

图 9 弧型地形上的波浪反射系数Fig. 9 Wave reflection coefficient of an arc-shape topography

4 结 论

本文建立了一改进型Boussinesq水波方程的数值模型，通过数值计算波浪在不同地形的传播变形，利用两点法分解出波浪的反射系数，考察了该方程在计算波浪反射问题的适用性，得出以下主要结论：

（1）本文建立的波浪水槽是低反射的，平地常水深情况下，无因次水深在 0.05～0.5之间，最大反射系数不超过 2%；无因次水深在区间[0.1，0.38]，反射系数值低于0. 5%。

（2）在模拟平斜坡上的波浪反射特性准确度较高，无因次水深小于0.05时，最大适用坡度为4∶1；无因次水深小于0.14时，最大适用坡度为4∶3；无因次水深小于0.39时，最大的适用坡度约为1∶2.5。

（3）在模拟双沙坝地形时，共振点的数值计算结果偏大。

（4）在模拟弧型地形上的波浪反射问题时，可达到的最大角度为40°。

此外本文的研究仅限于线性波浪的反射问题，有关非线性波浪反射的问题，将另行研究给出。

[1] 邹志利. 水波理论及其应用 [M]. 北京: 科技出版社, 2005.

[2] 王本龙. 基于高阶Boussinesq方程的海岸破波带数学模型研 [D].上海: 上海交通大学, 2005.

[3] Hong G W. High order models of nonlinear and dispersive wave in water of varying depth with arbitrary slopping bottom [J]. China Ocean Engineering, 1997, 11(3): 243-260.

[4] 刘忠波, 张日向, 姜萌. 简便推导改进 Boussinesq方程的一种方法 [J]. 大连理工大学学报, 2005, 45(1): 118-120.

[5] Suh K D, Lee C, Park W S. Time-dependent equations for wave propagation on rapidly varying topography [J]. Coastal Engineering,1997, 32: 91-117.

[6] 刘忠波, 邹志利, 孙昭晨. 适用于沙坝上 Bragg反射的二阶Boussinesq方程数学模型及其数值验证 [J]. 海洋通报, 2009,28(1): 75-80.

[7] Davies A G, Heathershershaw A D. Surface-wave propagation over sinusoidally varying topography [J]. Journal of Fluid Mechanics,1984, 144: 419-443.

[8] Guazzelli E, Rey V, Belzons M. Higher-order Bragg reflection of gravity surface waves by periodic beds [J]. Jounal of Fluid Mechanics, 1992, 245:301-317.

[9] Lee C, Park W S, Cho Y S, et al. Hyperbolic mild-slope equations extended to account for rapidly varying topography [J]. Coastal Engineering, 1998, 34: 243-257.

Applicability of one second-order Boussinesq model in the linear wave reflection problem

PU Gao-jun1,3, LIU Zhong-bo1,2, KANG Hai-gui1

(1. Dalian University of Technology, Dalian 116024, China; 2. Dalian Maritime University, Dalian 116024, China 3. Shengli Engineering & Consulting Co Ltd, Dongying 257026, China)

A numerical model in staggered grids was established based on the second order Boussinesq equations.Numerical simulations were carried out in a constant water depth in a flume, and the simulated wave reflection values were lower than 2%. The model was applied to calculate wave reflection from a plane slope, and the calculated reflection values were compared with analytical solution. Numerical results were larger than analytical solution only for steep cases in relative water depth, and numerical results agreed well with the analytical solution even for steep slope more than 1:1 in relative shallow water depth. Finally, the models were applied to Bragg reflection from a finite number of consecutive sills and wave reflection for wave propagating over arc-shape topography, and the numerical results were compared with the corresponding experimental results. The former comparison showed that the overall numerical results were in good agreement with the experimental results, but the reflection coefficients were clearly too large around the peak reflection for dual-resonance sills cases. And the latter comparison showed that when the arc terrain angle was over 40 degrees, the numerical results agreed well with the analytical results.

Boussinesq equations; wave; reflection

TV139.26

A

1001-6932(2011)06-0688-04

2010-09-05；

2011-06-13

蒲高军( 1964－ )，男，在读博士生, 高工，主要从事海洋工程研究。电子邮箱：liujinkun.slyt@sinopec.com。

康海贵，教授。电子邮箱：hgkang@dlut.edu.cn。