基于标准差准则的海底三维地形模型构建

韩富江，潘胜玲，王德刚，来向华

（1.国家海洋局第二海洋研究所，浙江 杭州 310012；2.南京大学 网络信息中心，江苏 南京 210093）

基于标准差准则的海底三维地形模型构建

韩富江1，潘胜玲2，王德刚1，来向华1

（1.国家海洋局第二海洋研究所，浙江 杭州 310012；2.南京大学 网络信息中心，江苏 南京 210093）

针对现有三角剖分需要投影到平面，局部优化时属性丢失的问题，本文采用一种顾及水深属性的三角剖分准则——标准差准则进行三角剖分，并且讨论了标准差的含义、标准差的计算以及标准差准则的描述。根据标准差准则，实现了一种基于标准差准则的海底三维地形模型构建方法。实验结果表明该方法提高了三角剖分的合理性，模型重建的细节与精确程度更高，在处理特殊地形上优于基于空外接圆准则的TIN模型构建方法。

标准差准则；海底三维地形模型；不规则三角网；特殊地形

虚拟海洋环境仿真是数字海洋建设的重要组成部分，它以数字的方式，逼真地模拟再现海洋环境，使人们可以探索有关海洋的自然和人文信息，并与之互动。而海底三维地形模型的构建是虚拟海洋环境仿真的关键技术，对虚拟海洋环境仿真的效果有着重要影响。

海底三维地形模型的构建通常采用数字地面模型（Digital Terrain Model，DTM）。目前，数字地面模型包括3种基本数据结构：等高线结构（Contour）、规则格网结构（Grid）以及不规则三角网结构（Triangulated Irregular Network，TIN）。基于等高线的DTM是由一系列等高线集合和其对应的高程值组成，等高线按有序的坐标点存储，可认为是带有高程属性的简单多边形或多边形弧段[1]。通过等高线和流线（等高线的法线方向）可把地形表面划分成不规则的多边形，有利于简化水文模型的分析计算[2]，因而等高线结构DTM在水文模型等地学分析领域应用较多。规则格网结构DTM计算处理简单，但不能准确表示地形的结构和细节，在地形平坦的地方，存在大量的数据冗余；在不改变格网大小的情况下，难以表达复杂地形的突变现象[3]。而不规则三角网结构TIN模型由于顶点分布的任意性，能够较好地反映地形表面特征及变化。TIN模型在表现地形表面起伏特征上具有规则格网无可比拟的优势。同时，由于TIN模型结构紧凑，在相同表现效果的前提下，TIN模型所需的顶点数目要少于规则格网模型，从而TIN模型的数据量往往要比规则格网模型的数据量要小得多[4]。因此，基于海量数据的海底三维地形模型构建通常采用TIN模型。

TIN模型构建的核心技术就是散点的三角剖分，三角剖分过程也就是TIN的构建过程。而三角剖分准则决定着三角形的几何形状和生成TIN模型的质量[5]，影响着模型所表达地形的逼真度和精度。目前常用的三角剖分准则有：最短距离和准则、对角线准则；Lee、Lawson提出的空外接圆准则、最大最小角准则、张角最大准则[6,7]；徐利治提出的面积比准则[8]等。理论上空外接圆准则、最大最小角准则、张角最大准则是等价的，可以保持三角网的唯一性，其余的则不然。对角线准则含有主观因素，现今已使用不多[5]。这些成果为TIN模型的构建研究提供了重要的借鉴和技术参考。然而这些传统的准则在进行散点集的三角剖分时，首先依据散点的平面分布确定一个三角网，然后将第三维数据如水深附加于平面三角网上，从而形成了包含连续的三角形面元的地形模型，因此它是一种面向曲面（三角形面元）的地形模型构建技术。面向曲面的模型构建方法，仅考虑了曲面元素的平面几何形状，而没有考虑其在空间的分布情况，当空间三角形与平面的夹角超过一定角度时，往往平面上形状较好的三角形在空间上其形状并不一定好，平面上形状不好的三角形在空间上其形状并不一定不好；另外一个问题是二维平面上的三角剖分忽略了点的属性值，导致局部优化过程（Local Optimization Procedure，LOP）中数据点的属性丢失，造成在特殊地形如陡崖、虎口等处构建的TIN模型与实际地表不相符。

为了解决上述问题，本文采用标准差准则[9]，将散点三维数据（x,y,h）计算得到的标准差，作为判断三角形形状在空间上好坏的依据，该准则将水深值引入三角剖分过程，提高了剖分的合理性。同时，在分析总结现有TIN剖分准则和算法的基础上，实现了一种基于标准差准则的海底三维地形模型构建方法，并实验证明该方法构建的海底三维地形模型更能反映海底的真实地表。

1 标准差准则

1.1 标准差的含义

标准差是一种量度数据分散程度的标准，用于衡量一组数据对算术平均值的离散程度。标准差较大，表示大部分数据与算术平均值之间的差异较大；标准差较小，表示这些数据较接近算术平均值。在TIN模型的构建过程中，标准差则是衡量一个三角形接近正三角形程度的标准。对于一个三角形而言，三角形的三个顶角角度作为样本数据，其算术平均值为60°，计算出的标准差越小表示三角形的三个顶角越接近60°，也意味着该三角形越接近正三角形，符合了TIN模型中三角形的几何形状尽量接近正三角形的剖分原则。

1.2 标准差的计算

在概率论与数理统计中，离散型随机变量的标准差计算公式[10]为：

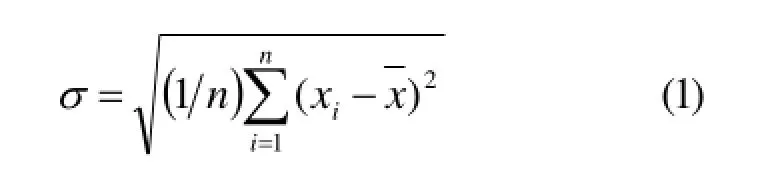
其中n表示随机变量的个数；为n个随机变量的算术平均值。对于TIN模型中的一个三角形ABC而言（图1），假设三个顶点坐标为A（x1，y1，h1），B（x2，y2，h2），C（x3，y3，h3）,三个顶角为A、B、C，其算术平均值为60°,则标准差的计算公式（1）可以改写为：

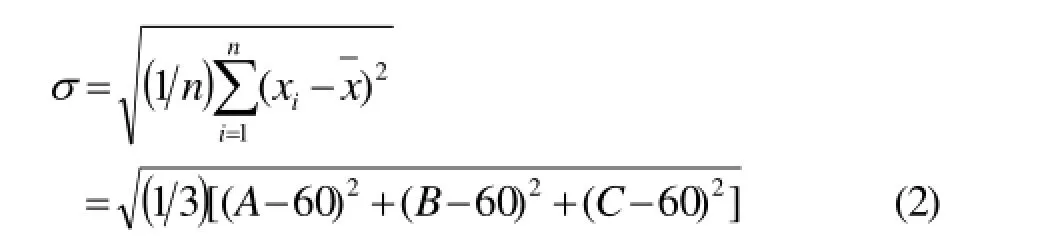
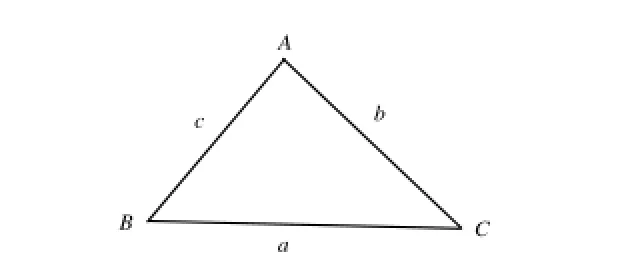
图 1 三角形示意图Fig.1 Triangle sketch

式(2)中的A、B、C表示三角形的三个顶角，可由三角形的余弦定理求得：

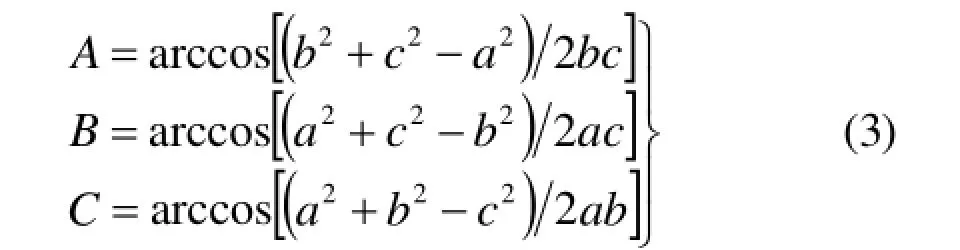
式(3)中的a、b、c表示三角形的三条边长，可由空间两点的距离公式求得：

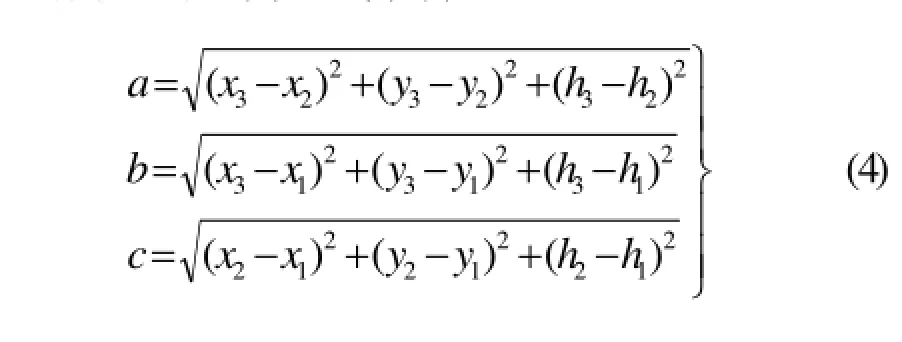
1.3 标准差准则描述

标准差准则就是TIN模型构建中一种三角形的剖分法则，指在两相邻三角形形成的凸四边形中，这两三角形的标准差之和一定小于交换凸四边形对角线后所形成的两三角形的标准差之和。利用标准差准则进行三角形剖分时，原始空间数据的三维坐标（x,y,h）参与三角形形状好坏的判断，不需要投影到平面上，直接从空间上进行三角剖分，剖分结果更符合空间实际的地形表面。

标准差准则的基本思想是将空间4点组成的四边形进行三角剖分划分为了两种情形a和b（图2），分别计算两种情形下的三角形标准差之和，如果情形a的三角形标准差之和小于情形b的两个三角形标准差之和，根据TIN模型中三角形的几何形状尽量接近正三角形的原则，选择情形a作为构建TIN的三角形，否则，选择情形b。

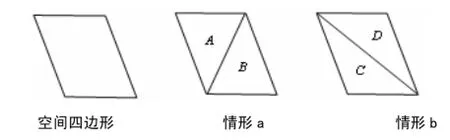
图 2 标准差准则Fig.2 Standard deviation criterion

对情形a和情形b中的三角形A、B、C、D以其内角的角度作为样本数据，根据公式(2)分别计算其标准差，用σA、σB、σC、σD表示。则情形a中A、B两个三角形的标准差之和为σA+σB；情形b中C、D两个三角形的标准差之和为σC+σD。根据标准差准则，可以通过判断σA+σB与σC+σD的大小，选择情形a还是情形b作为构建TIN模型的优化三角形。如果（σA+σB）－（σC+σD）小于零，则情形a好；（σA+σB）－（σC+σD）大于零，则情形b好；（σA+σB）－（σC+σD）等于零，则两种情形一样好，选择情形a或是情形b都可以。

2 基于标准差准则的海底三维地形模型构建

一个良好的数据结构和三角形剖分准则，必须有高效的算法和程序实现。目前离散型数据集的TIN模型构建使用最为广泛的是Delaunay直接三角剖分算法，包括分割合并算法、三角网增长算法和逐点插入算法[5]。由于分割合并算法是递归执行，内存开销较大；三角网增长算法最大的问题是计算的时间复杂性，数据点越多问题越突出[11]；而逐点插入算法在很大程度上克服了上述问题，并且概念简单，容易实现，还能够进行约束三角剖分，所以本文构建海底三维地形模型的方法沿用了逐点插入法的基本思想，只是把LOP时采用的空外接圆准则替换为标准差准则，在空间上直接对散点进行剖分，提高模型重建的细节与精确度。

算法的基本思想是：先在包含所有数据点的多边形中建立初始三角网，然后在已存在的三角网中插入数据点，找到包含该数据点的三角形，连接该点与其所在三角形的三个顶点形成新的三个三角形，用标准差准则优化新形成的三角形，直至所有数据点都插入到三角网中。具体的算法步骤如下：

步骤1 建立包含所有数据点的初始包容盒，该包容盒可以为凸壳、矩形包容盒或超级三角形，并对该包容盒进行初始三角剖分。本文选用的包容盒为超级三角形，超级三角形的三个顶点坐标可以通过以下方法得到。假设离散数据集中含有n个离散点，坐标为（xi，yi，hi），i=1,2,…,n。对离散点的坐标进行比较得到最大值xmax，ymax，最小值xmin，ymin，hi为水深值。通过以下公式计算得到坐标范围dx，dy，坐标范围最大值dmax以及坐标中间值xmid，ymid。

步骤2 往初始三角网中插入数据点，设当前处理数据点为P，首先找出包含点P的三角形T，设T的三顶点为V1、V2、V3，然后P与T三顶点相连，形成三个新的三角形T1、T2、T3，如图3所示。

步骤3 对所有新形成的三角形，利用标准差准则进行优化处理。为了对所形成的新三角形进行优化，需要将包含当前点的三角形的相邻三角形放入一个堆栈中。然后从堆栈中每次弹出一个三角形，与包含插入点的三角形进行LOP优化，如果进行了对角线交换，相邻三角形也要放入堆栈，这是一个循环过程，直到堆栈为空，方可进行下一点的处理。具体优化过程如下：

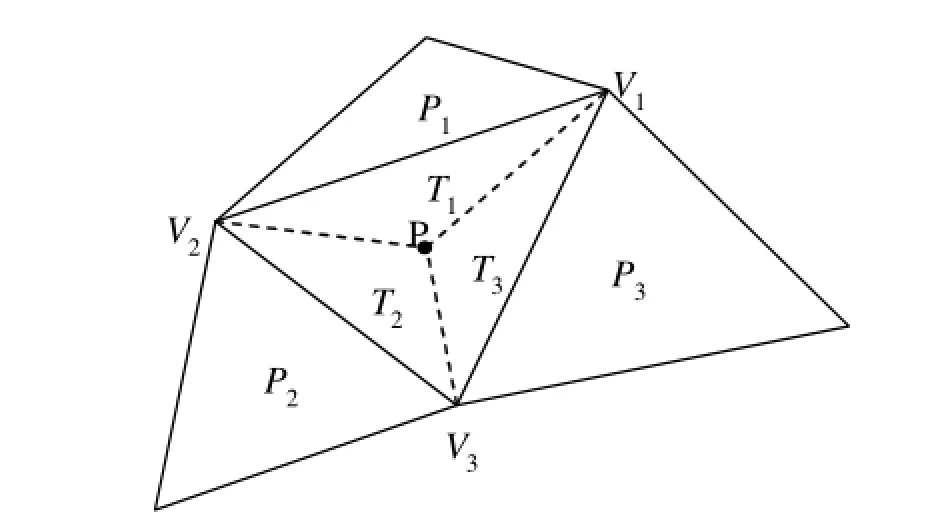
图 3 包含点P的三角形及初始三角剖分Fig.3 Triangle including point P and initial triangulation

（1）把包含P的三角形的三个邻接三角形P1、P2、P3放入堆栈中；

（2）从堆栈中弹出三角形P3；

（3）计算三角形P3与邻接三角形T3的标准差之和σ1，以及交换对角线之后两个三角形的标准差之和σ2。如果σ1大于σ2，则需要交换对角线，否则，弹出下一个三角形；

（4）如果交换对角线，原来与P3相邻的两个三角形也要压入堆栈；

（5）重复（2）－（4），直到堆栈为空，则P点的插入过程结束。

步骤4 重复步骤（2）－（3），直至所有数据点都被插入到TIN模型中。

步骤5 处理外围三角形，完成海底三维地形模型的构建。由于超级三角形的顶点并不是水深离散点集中的点，所以要将包含超级三角形顶点的三角形和超级三角形的三个顶点移除，得到最终的海底三维地形TIN模型。

基于标准差准则的海底三维地形模型构建方法较好地解决了LOP时水深属性丢失的问题，同时，对数据点的三角剖分直接在空间进行，提高了海底地形TIN模型的细节性和准确性。

3 实验与分析

为了验证基于标准差准则海底三维地形模型构建方法的优越性，本文在C#.NET开发环境中编程实现了该方法，构建了海底三维地形TIN模型，并且与利用空外接圆准则构建的海底三维地形模型进行了对比分析。实验选取的数据为由SeaBeam 2112多波束测深系统测得的水深数据，共有5 844个数据点，数据分布比较均匀，数据点的三维显示如图4所示。由图4可以看出本文所选实验区的海底地形起伏变化较大，并且还有一个特殊地形陡崖。

图4 水深数据点的三维显示Fig.4 Three-dimensional display of bathymetric data points

基于标准差准则算法构建的海底三维地形TIN模型如图5（a）所示；空外接圆准则算法构建的海底三维地形TIN模型如图5（b）所示。

由图5（a）可以看出，基于标准差准则算法构建的海底三维地形TIN模型有效地避免了狭长三角形的出现，保证了三角形形状在空间上的良好性，解决了水深属性丢失的问题，使得在特殊地形陡崖处构建的TIN更接近海底的真实地表。而空外接圆准则算法构建的海底三维地形模型，由于其三角剖分过程是在投影平面上进行，造成陡崖处的TIN很凌乱，狭长三角形较多，不符合三角剖分的原则，也不能反映特殊地形的真实表面，结果如图5（b）所示。两种方法构建的海底三维地形模型不一致的主要原因是在利用空外接圆准则对TIN模型进行优化的过程中，只用到了数据点的（x,y）坐标，没有顾及水深属性，并且需要投影到平面xoy上进行，这样就造成在空间上形状较好的三角形，投影到平面上反而变成了狭长三角形；空间上狭长的三角形，投影到平面上反而接近正三角形。特别是在陡崖等特殊地形，上部的数据点投影到平面上还有可能与下部数据点重合或相邻较近，在三角剖分过程中，容易引起狭长三角形的形成。基于标准差准则的算法则直接在空间对水深数据点进行三角剖分，利用数据点三维坐标（x,y,h）计算得到的标准差作为判断三角形形状好坏的依据，剖分准则顾及了海底地形的属性水深值，提高了海底地形三维TIN模型的细节性和准确性。

图5 两种剖分准则构建的海底三维地形模型透视图对比Fig.5 Contrast of three-dimensional seabed terrain model constructed by different algorithms

4 结 语

本文在分析现有三角剖分准则的基础上，采用一种顾及水深属性的三角剖分准则—标准差准则进行三角剖分，该准则克服了原有剖分准则需要投影到平面上进行三角剖分的不足，解决了LOP时属性丢失的问题。根据标准差准则，实现了一种基于标准差准则的海底三维地形模型构建方法。实验结果表明该方法提高了三角剖分的合理性，模型重建的细节与精确程度更高，在处理特殊地形上优于基于空外接圆准则的TIN模型构建方法。由于水深测量数据的海量性，基于标准差准则的海底三维地形模型的构建效率以及模型的纹理映射处理都需要进一步的深入研究。

[1]Moore I D, Grayson R B.Terrain-based Catchment Partitioning and Runoff Prediction Using Vector Elevation Data [J].Water Resources Research.1991b, 27(6):1177-1191.

[2]Wilson J P, Gallant J C.Terrain Analysis: Principles and Applications [M].New York: John Wiley and Sons, 2000.

[3]邬伦, 刘瑜, 张晶, 等.地理信息系统-原理、方法和应用 [M].北京: 科学出版社, 2001.

[4]石松.虚拟地理环境中地形建模及其空间分析研究 [D].福州:福州大学, 2005.

[5]汤国安, 刘学军, 闾国年.数字高程模型及地学分析的原理与方法 [M].北京: 科学出版社, 2005.

[6]Lee D T, Schachter B J.Two Algorithms for Constructing a Delaunay Triangulation [J].Int.Journal of Computer and Information science.1980, 9(3): 219-242.

[7]Lawson C L.Software for c' Surface Interpolation [C]//Mathematical Software III, New York: Academic Press, 1977: 161-194.

[8]徐利治.逼近论 [M].北京: 国防工业版社, 1985.

[9]潘胜玲, 刘学军.基于标准差的地形三维表面模型建立方法 [J].计算机应用研究, 2007, 24(11): 295-297.

[10]余锦华, 石北源, 杨维权.概率论与数理统计[M].广州: 中山大学出版社, 2000.

[11]李志林, 朱庆.数字高程模型 [M].武汉: 武汉大学出版社, 2003.

Construction of 3D Seabed Terrain Model based on the Standard Deviation Criterion

HAN Fu-jiang1, PAN Sheng-ling2, WANG De-gang1, LAI Xiang-hua1

(1.Second Institute of Oceanography, SOA, Hangzhou 310012, China; 2.Network Information Center, Nanjing University, Nanjing 210093, China)

At present, existing triangulation must be done in the projection plane, so it causes the loss of attribution information in LOP (Local Optimization Procedure).In this paper, a new triangulation criterion based on standard deviation is used.The definition of standard deviation, calculation of standard deviation, and description of standard deviation criterion is investigated.Then the construction algorithm of 3D seabed terrain model based on standard deviation is presented according to the standard deviation criterion.The result of experiment shows that this method improves the rationality of triangulation, the details and precision of seabed terrain model are better than others, and it is better in dealing with special terrain than the algorithm based on empty circum-circle criterion.

standard deviation criterion; three-dimensional seabed terrain model; Triangulated Irregular Network; special terrain

TP311

A

1001-6932(2011)06-0674-05

2011-01-05；

2011-05-23

国家海洋局第二海洋研究所基本科研业务费专项资金资助项目（JG0913, JT0803, JG0911）。

韩富江（1977－），男，硕士，工程师，主要从事三维建模及可视化、海洋测绘、DEM及地形分析方面的研究。电子邮箱: hfj111@126.com。