潜堤上破碎波浪传播变形的数值模型及其验证

刘忠波，于德海，孙昭晨

（1.大连海事大学 交通运输装备与海洋工程学院, 辽宁 大连116026; 2.大连理工大学 海岸和近海工程国家重点实验室, 辽宁 大连116024）

潜堤上破碎波浪传播变形的数值模型及其验证

刘忠波1,2，于德海1，孙昭晨2

（1.大连海事大学 交通运输装备与海洋工程学院, 辽宁 大连116026; 2.大连理工大学 海岸和近海工程国家重点实验室, 辽宁 大连116024）

为模拟潜堤上破碎波浪传播时产生能量的耗散这一特性，在改进的具有四阶色散的Boussinesq水波方程中引入二阶紊动粘性项，建立了考虑波浪破碎的水波数学模型。在非交错网格下建立了有限差分数值模型，并利用三阶Adams-Bashforth格式预报、四阶Adams-Mouton格式校正对数值模型进行求解。通过数值试验，模拟了不同坡度的潜堤上破碎波浪传播变形，并将数值计算波面时间历程与实验结果进行了比较，二者基本吻合，这说明在四阶Boussinesq水波模型中引入二阶粘性项来考虑波浪破碎引起能量耗散的做法是有效的。

Boussinesq方程；破碎波；紊动粘性

波浪向近岸传播中，波浪经历浅水、折射、绕射、反射等复杂的现象，当波高与水深达到一定比例时，波浪产生破碎。为模拟这一复杂的破碎现象，近年来许多学者对此进行了研究，这些研究中常用到的模型有Navier-Stokes方程数值模型、引入考虑能量耗散的Boussinesq方程数值模型和缓坡方程数值模型等[1-5]。尽管Navier-Stokes方程在解释波浪破碎这一过程中非常精确，但因其求解速度慢，很难应用到实际工程中去，而Boussinesq方程、缓坡方程由于计算速度较快，在实际工程中得到了广泛的应用。波浪在通过人工潜堤顶部时，由于水深变小，波高增大，波浪可能会产生破碎，破碎后波高会有所减少，因此通常利用潜堤上波浪破碎这一消浪特性从而达到诸如保护海岸、保证港口船舶泊稳条件等目的。缓坡方程能给出较为准确的统计性均方波高、增水减水等，潜堤上的波浪往往带有较强的非线性，对于某一具体位置点，此类方程很难给出精确的波浪时间历程。Boussinesq方程，尤其是含高阶非线性和高精度色散性的Boussinesq方程，能很好的模拟波浪破碎前的强非线性这一现象，而引入破碎项后的Boussinesq方程，对模拟波浪破碎后在潜堤后的空间点的时间历程又将如何，这是一个需要考虑的问题。为更好地模拟更大适用水深下波浪传播变形问题，刘忠波等拓展了适合复杂地形的Boussinesq水波方程[6]，并通过潜堤上波浪不破碎的实验验证了其数值模型。由于缺少破碎项，该方程数值模型不能用于模拟波浪破碎现象。当引入能考虑波浪破碎引起的能量耗散项时，这一模型模拟的效果如何，是本文研究的重点。

1 考虑波浪破碎的Boussinesq数值模型

刘忠波等推导了加强的适合复杂地形的Boussinesq方程[6]，当引入考虑波浪破碎的紊动粘性项后，方程的一维数学模型可写为：

其中f(x,t)、fsponge分别为内部造波源项和边界消波项，本文直接引用文献[6]的结果。fbreak，fbottom分别为紊动粘性项和底摩擦项。本文则采用Kennedy等的研究成果[3]，该紊动粘性项的表达式如下：

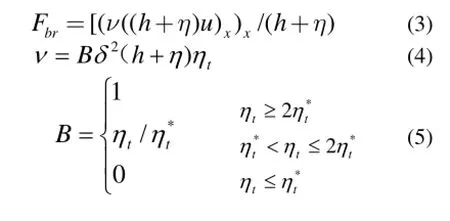
在本文的数值算例针对潜堤上波浪破碎进行的，所给的参数将不同于Kennedy等给出的系数，这些系数将在数值研究中给出。针对(1)和(2)中导数差分格式及求解过程同文献[6]。

2 算 例

2.1 实验介绍

文献[7]中的物理模型实验在大连理工大学海岸和近海工程国家重点实验室的波浪水槽中进行。水槽长23 m、宽0.8 m、高0.8 m，水槽中设置一个梯形潜堤，实验中地形布置的情况见图1。最大水深为0.4 m（最小水深为0.1 m），波浪要素见表1，按1:25比例换算，相当于实际水深10 m，波高为1 m，波浪周期为8 s, 9 s和10.1 s。

表 1 实验波浪要素Tab.1 Wave parameters in experiment

2.2 数值结果对比与分析

在计算中本文数值研究的对象是潜堤上波浪的破碎和传播，波浪破碎仅局限于潜堤顶部局部区域，这与海岸斜坡上波浪连续破碎不同。当采用较大的启动系数时，在x=9.5 m处（含该点）后的波浪模拟效果相对较大，波浪破碎少，与实验结果吻合较差，由于篇幅限制，本文就不对此问题进行过多阐述；同时，尽管波浪在x=8.5 m处发现浪花，但微碎后的波高幅度并不减少，在模拟中采用此点以前不启动波浪破碎。最终对破碎项中出现的系数取为：中的系数取0.25~0.35，其中模拟周期为1.6 s的波况时，采用0.35，而模拟周期为1.8 s和 2.02 s时，采用0.25，中的系数为0.15，破碎系数δ为1.6，针对以上实验进行了数值计算，数值结果和实验结果的对比见图2－图7。

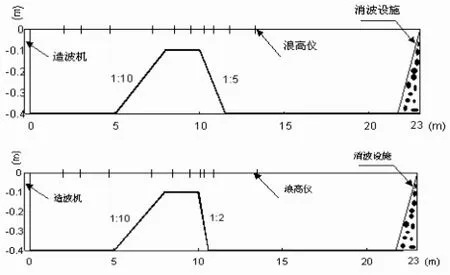
图 1 实验布置图Fig.1 Experimental set-up

由图2－图7综合来看，数值模拟结果与实验结果基本吻合。下面就这些图中数值结果与实验结果对比情况做一下具体分析。在x=2.0 m、3.0 m、4.7 m和7.25 m处，波浪不破碎，数值结果与实验结果相位吻合较好，但幅值略存在一些差异。前者说明本文采用的Boussinesq方程在这些情况下适用，后者存在差别的主要原因是数值模拟中采用了内部造波法，而实验是采用了边界造波。波浪在爬到潜堤顶上后，在实验中x=8.5 m观察到在潜堤前部开始出现水花现象，但是即便在此点以前不考虑波浪时模拟的结果与实验结果在幅值上存在差异，这可能是由于波浪破碎时产生的水花对浪高仪记录的数据产生影响造成的。在x=9.5 m处以后，无论是从幅值还是从相位上来看，数值模拟结果和实验结果存在差异，不仅幅值存在差异，相位也存在差异，其在周期为2.02 s的两组计算中尤为明显，详细可见图4和图7中在x=13.5 m处的对比情况上。幅值上的差异主要反映出本文所采用的模型本身引入紊动粘性来考虑波浪破碎这一本质特性的限制，而波浪存在的相位差异变化可能是：除了模型破碎这一特性限制引起的，由于破碎时波浪非线性强，潜堤顶部的波高较大，这引起Boussinesq方程的色散关系发生频散现象，而且当波浪穿过潜堤由浅水到深水传播时，各次谐波又以自由波传播，因此波形上出现了以上的差异。

图 2 数值与实验的波面时间历程图对比（右坡坡度1:2，周期1.6s）Fig.2 Comparisons of computed surface elevation and experimental data

图 3 数值与实验的波面时间历程图对比（右坡坡度1:2，周期1.8s） Fig.3 Comparisons of computed surface elevation and experimental data

图 4 数值与实验的波面时间历程图对比（右坡坡度1:2，周期2.02sFig.4 Comparisons of computed surface elevation and experimental data

图 5 数值与实验的波面时间历程图对比（右坡坡度1：5，周期1.6s） Fig.5 Comparisons of computed surface elevation and experimental data

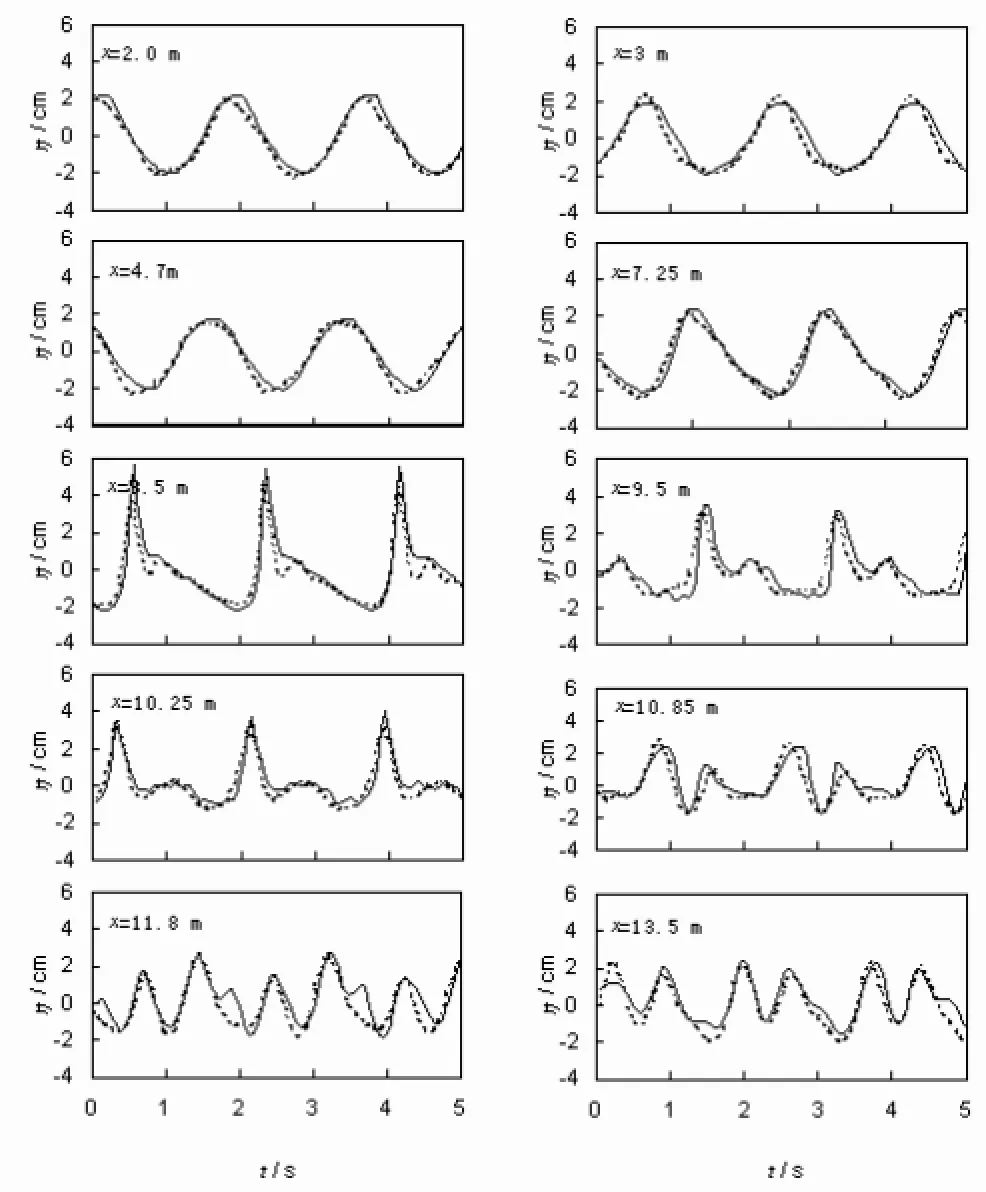
图 6 数值与实验的波面时间历程图对比（右坡坡度1:5，周期1.8sFig.6 Comparisons of computed surface elevation and experimental data

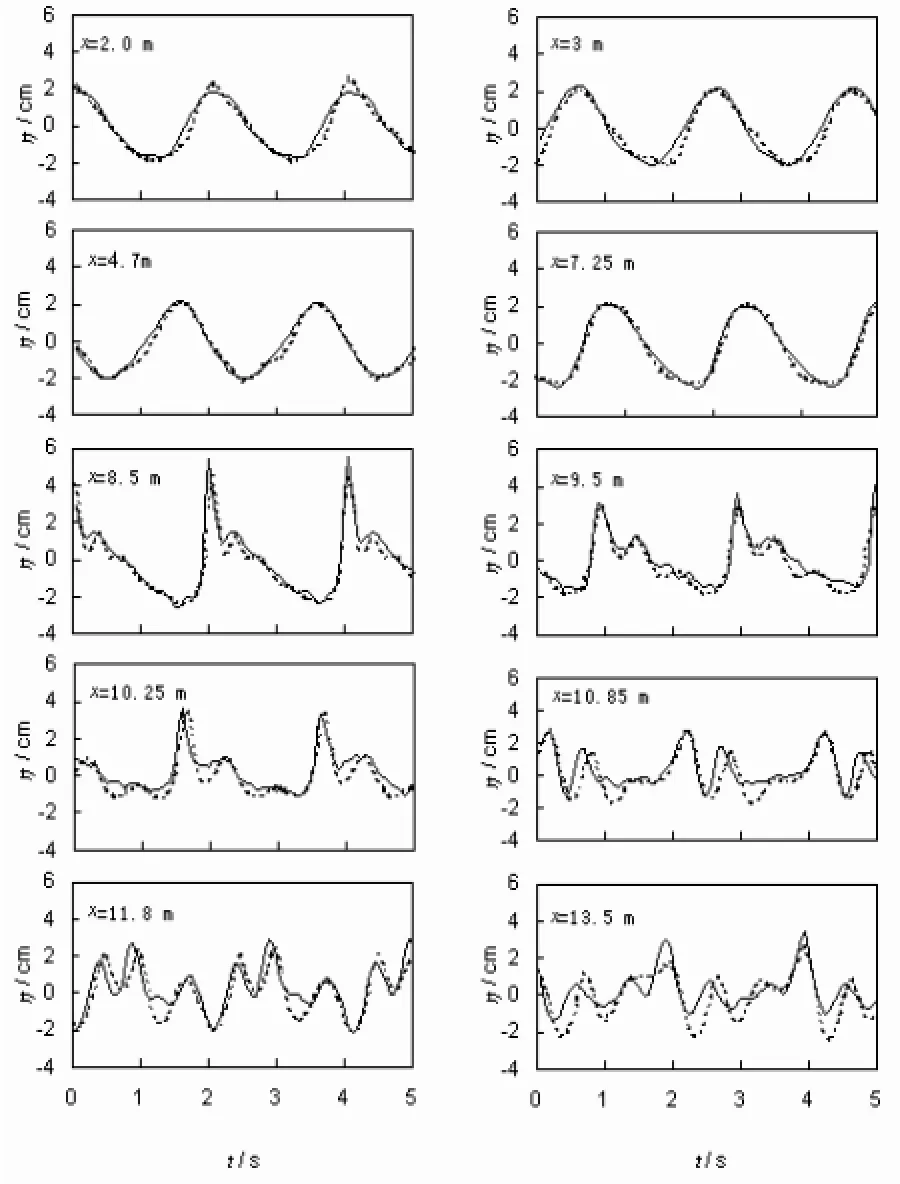
图 7 数值与实验的波面时间历程图对比（右坡坡度1:5，周期2.02s）Fig.7 Comparisons of computed surface elevation and experimental data

3 结 论

本文基于加强的适合复杂地形方程，引入了紊动粘性项来考虑波浪破碎，建立了一维波浪破碎数值模型，研究了破碎波浪在潜堤上传播变形这一过程。通过本文研究得出如下结论：

（1）数值结果与实验结果基本吻合，这说明引入了紊动粘性项来考虑波浪破碎的方法不仅在二阶Boussinesq方程数值模型中适用，在本文所采用的四阶色散Boussinesq模型中同样也适用。

（2）利用本文模型模拟潜堤上波浪破碎时，所采用紊动粘性项中的启动系数比Kennedy等在计算平缓斜坡时采用的系数要小，本文模型在计算潜堤上破碎波时采用的前系数为0.25～0.35，破碎系数为1.6。

（3）实验中波浪水槽长23 m，边界反射波和造波板的二次反射效应对采集的实验数据会产生一定的影响，为进一步给出定量的对比与分析，在更长的水槽中进行有关波浪破碎的实验仍待进一步深入研究。

[1]Lin P, Liu P L F.A numerical study of breaking waves in the surf zone [J].J Fluid Mech, 1998, 359: 239-264.

[2]Schaffer H A, Madsen P A, Deiggard R A.A Boussinesq model for waves breaking in shallow water [J].Coastal Eng, 1993, 20: 185-202.

[3]Kennedy A B, Qin C, Kirby J T, et al.Boussinesq Modeling of Wave Transformation, Breaking, and Runup.I:1D [J].J Wtrw Port Costal and Oc Eng, 2000, 126(1): 39-47.

[4]李绍武, 李春颖, 谷汉斌, 等.一种改进的近岸波浪破碎数值模型 [J].水科学进展, 2005,16(1): 36-41.

[5]Svendsen I A, Yu K, Veeramony J.A Boussinesq breaking wave model with vorticity.Proceedings of the 25th International Conference on Coastal Engineering [C].New York: ASCE, 1996: 1192-1204.

[6]刘忠波, 邹志利, 孙昭晨.加强的适合复杂地形的水波方程及其一维数值模型验证 [J].海洋学报, 2008, 30(3): 117-125.

[7]张晓莉.应用高阶Boussinesq方程模拟复杂地形上波浪传播与变形 [D].大连: 大连理工大学, 2001.

Numerical model of breaking waves propagating over a submerged breakwater and its laboratory validation

LIU Zhong-bo1,2, YU De-hai1, SUN Zhao-chen2

(1.Transportation Equipment and Ocean Engineering College, Dalian Maritime University, Liaoning 116026, China; 2.State Key Laboratory of Coastal and Offshore Engineering, Dalian University of Technology, Liaoning 116024, China)

To model the breaking waves propagating over a submerged breakwater and consider the energy dissipation by breaking property, the mathematical model for breaking waves was given by adding the second order eddy viscosity terms to the fourth order dispersive Boussinesq equations.Numerical model was established with finite differential method in non-staggered grid, and the model was solved with the third-order Adams-Bashforth predictor and the fourth-order Adams-Moulton Corrector in time marching.Numerical simulations were carried upon breaking wave evolution over a submerged breakwater with different back slopes.The computed surface elevations varying with time history in different locations were compared to experimental data, and the agreement was reasonably satisfactory, and this demonstrated that the present method to consider energy dissipation in Boussinesq wave model was effective.

Boussinesq eqautions; breaking waves; eddy viscosity

P731.22

A

1001-6932(2011)06-0633-04

2010-08-09；

2011-03-22

中国自然科学基金 (40902075)。

刘忠波 ( 1976－ )，男，博士，主要从事水波理论及数值模拟研究。电子邮箱：zhongbo_liu1976@163.com。