碳钢轴类零件激光熔覆弯曲的定量实验研究

郑 晖，韩志仁，陈 江，王国栋

(1.东北大学 轧制技术及连轧自动化国家重点实验室，沈阳 110004;2.沈阳航空航天大学 航宇学院，沈阳 110136;3.沈阳大陆科技园，沈阳 110136)

碳钢轴类零件激光熔覆弯曲的定量实验研究

郑 晖1，2，韩志仁2，陈 江3，王国栋1

(1.东北大学 轧制技术及连轧自动化国家重点实验室，沈阳 110004;2.沈阳航空航天大学 航宇学院，沈阳 110136;3.沈阳大陆科技园，沈阳 110136)

为了得到不同激光熔覆面积下轴弯曲量的变化情况，得到轴类零件激光熔覆弯曲过程的数学模型，得出熔覆面积与轴弯曲程度之间的经验公式，设计了激光熔覆校轴实验.实验在相同熔覆长度和深度下，改变熔覆中心角，即熔覆面积，进行激光熔覆.实验结果表明，在激光熔覆校轴中，轴发生了朝向激光束的弯曲;熔覆层所对中心角小于90(°)时，轴弯曲量与熔覆面积成正比关系，使轴弯曲量达到最大的熔覆层所对中心角为90(°);同时得到了激光熔覆校轴的数学模型和衡量轴弯曲量的参数，得出轴弯曲量与熔覆面积的经验公式，得出不同位置处轴跳动值的经验公式.通过经验公式计算得出的轴跳动值与实测的轴跳动值拟合良好，最大的误差为0.032 mm，总平均误差为0.001 mm，由此说明抽象出的弯曲数学模型正确，经验公式精度较高.

激光技术;校轴;激光熔覆;数学模型;经验公式

所谓“再制造”是指把达到使用寿命的产品通过修复使其达到甚至超过原产品性能的加工过程.国外再制造工程从诞生至今虽仅有50多年的历史，但其发展迅速，现已作为一独具特色的新兴产业成为制造业的重要组成部分.我国再制造产业处于起步阶段，与发达国家有很大差距.上世纪90年代后期，开始受到企业界的认同与支持［1］.

轴是机械装置的一种重要零件，支撑着其他转动件并传递扭矩.轴的制造精度直接影响到机械运行的平稳性［2］.在运行中，由于各部件的温差而产生热应力，过大的热应力会使轴发生永久弯曲［2～3］;另外，对机械的使用不当，如紧急停车可能使轴发生永久弯曲.如果加工一根新轴，不仅成本高，而且工期长，会造成企业较大经济损失.转而考虑再制造技术对弯曲轴进行校直，可以节约成本，缩短生产周期，使轴重新达到使用标准，也为加工新轴争取到宝贵的时间.

考虑采用激光熔覆的方法进行校轴，是因为激光熔覆技术校轴加工速度快，热影响区小，后续加工量小并且极易与数控系统配合实现自动化［4～5］.实际生产中激光熔覆校轴技术的应用，往往仅依靠工人经验，采取逐步增加熔覆区域的方法，边熔覆边检测，这样不仅浪费工时，而且增加成本.为了解决这个问题，需要得出熔覆参数对轴弯曲程度的影响的经验公式，以使熔覆之前就能较准确地设定各种参数，减少后续的工作.

1 实验

1.1 实验目的

为了掌握激光熔覆校轴的规律性，得到工艺参数与轴弯曲量的关系，需要设计实验进行研究，因为很难将几根实验轴弯曲相同程度用于比较研究，所以换一角度考虑问题，由于激光熔覆后直轴会发生不同程度的弯曲，弯曲量常采用轴的径向圆跳动值(轴在某一固定参考点绕基准轴线旋转一周时，百分表的最大变动量)来衡量，简称为轴跳动值.根据轴跳动值的变化规律，得到轴类零件激光熔覆后弯曲的参考数据，对此数据进行分析比较也可以得到激光熔覆校轴的规律性.因此设计了如下实验:

(1)确定激光熔覆时使轴弯曲量达到最大的熔覆层所对应的中心角α，以下简称中心角.

(2)得到轴类零件激光熔覆弯曲的数学模型，确定衡量弯曲程度的指标，从而得到弯曲程度与熔覆面积之间定量关系的经验公式.

1.2 实验材料及设备

本实验选用直轴，如图1所示，材料为45﹟钢，该轴的原始轴跳动值各处均在0.01 mm.实验设备为沈阳大陆集团的DL－HJ－T5000激光器，DL－LPM－Ⅲ激光数控加工机;检测轴跳动值在M1350Φ500 mm×3000 mm的外圆磨床上进行，检测设备为百分表.

1.3 实验方案确定

熔覆深度取为2 mm，熔覆层中心角α取6个.通过分析可知，熔覆区域大，零件弯曲程度也大.而轴类零件是轴对称零件，熔覆区域过大，会使弯曲存在左右抵消现象，反而会减小弯曲量.同时借鉴火焰校直的实践，校直时的加热区域一般不会超过120(°)(轴圆周方向的三分之一)，所以选择了6个中心角度，分别为30(°)，45(°)，60(°)，75(°)，90(°)和 120(°)，如图 1 所示.考虑加工方便以及实验数据可比性，在轴的0(°)相位前后α/2范围内加工深度均匀且为2 mm的熔覆槽，槽的长度统一取为230 mm，一边留出10 mm用作测量.检测工艺轴的轴跳动值和弯曲后高点相位.

图1 实验轴示意图Fig.1 Schematic diagram of the shaft specimen

1.4 实验过程

(1)吊装轴放在DL－LPM－Ⅲ激光数控加工机两顶尖之间，用四爪卡盘夹紧.轴用一顶尖加两滚轮拖住的形式，考虑轴变形不受限制.

(2)调设备DL－HJ－T5000的功率P、激光扫描速度v、焦距、光斑大小和熔覆层数n.基本实验参数为P=4 kW，v=7 mm/s，焦距为180 mm，光斑Ф5 mm，熔覆层数n=4，搭接2 mm;

(3)清洁槽表面，水平仪找水平，预置粉均匀，厚约2 mm.

(4)激光熔覆.

(5)等轴彻底冷却，再吊装轴到外圆磨床M1350Φ500 mm×3000 mm上，检测淬火处的硬度值.用百分表测量轴跳动值及高点相位.

(6)根据不同的α角，重复进行上面的步骤共6次.

2 熔覆层对应的中心角α对轴跳动值的影响

从图2可知，最大轴跳动值位于熔覆区域右侧，随着熔覆中心角α的增大，最大轴跳动值增大.且当α小于90(°)时，最大轴跳动值增大的幅度近似为一固定值;当α大于90(°)时，最大轴跳动值仍有增加但增大效果不明显.由此可以判断，能使弯曲量达到最大的熔覆中心角度α为90(°)，即90(°)为最优激光熔覆中心角.

通过测量，得出轴跳动值高点均出现在180(°)相位处，说明轴在激光熔覆后发生了朝向激光束的弯曲变形.

图2 熔覆中心角度α不同时的轴跳动值Fig.2 Eccentricity along the axial length at the different laser cladding center angle

3 经验公式的确定

要想得出经验公式来，首先需要找到一个可以表示轴弯曲程度的量，这个量与轴的长度无关.同时建立轴弯曲的几何模型，见图3.从图3可以看出熔覆后的轴在熔覆区是弯曲的，在熔覆区外基本是直线，即假定轴只在熔覆区产生了弯曲，其他地方有跳动值的改变是由于弯曲部分的带弯，因此可用弯曲部分弧线所对中心角的一半β来表示轴弯曲的程度.通过几何关系计算得出不同熔覆中心角的情况下的β值以及tan β值.

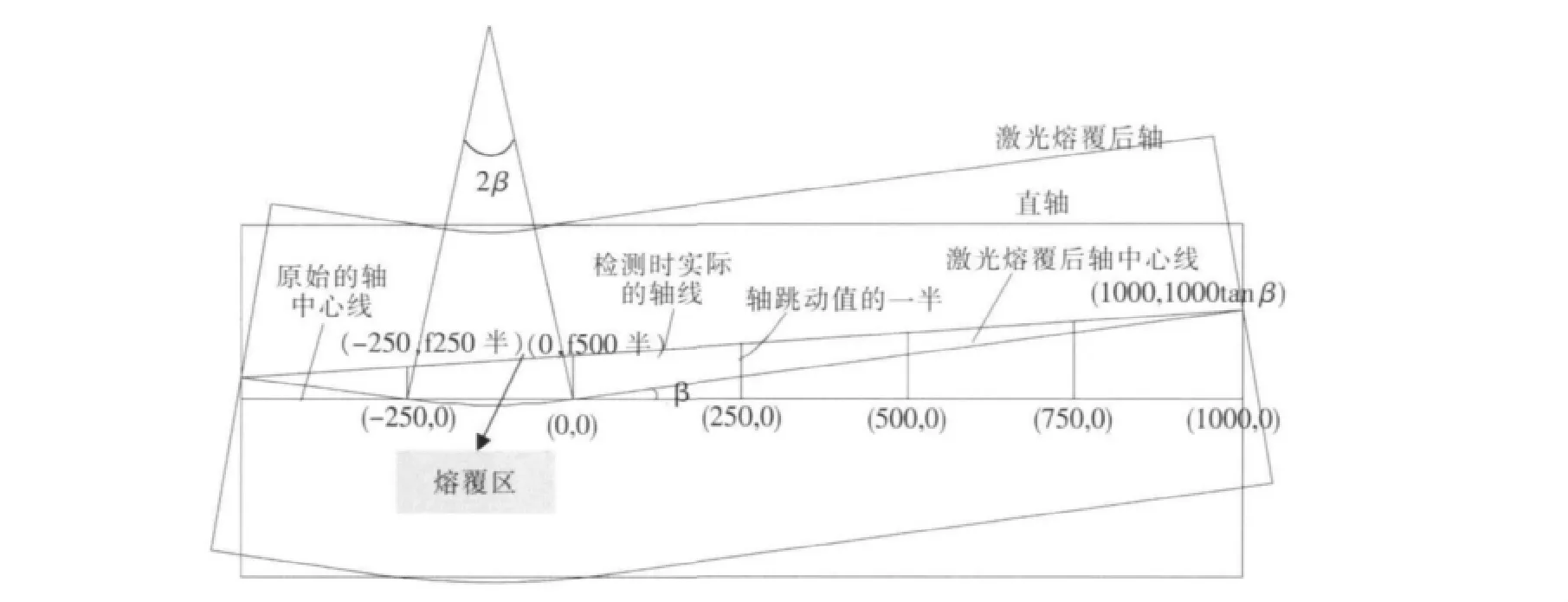
图3 轴激光熔覆后弯曲的数学描述Fig.3 Mthematical model of laser cladding bending of the shaft

表1 各次实验的工艺参数和对应的弯曲程度Table 1 Processing parameter for the test and the corresponding bending degree

由表1可以得出熔覆面积与轴弯曲量之间的曲线如图4所示:

从图4中也能看出，熔覆中心角α增大到90°后，弯曲量不再增大，而且熔覆中心角在90°内对弯曲程度的影响近似线性关系，反映在熔覆面积上如图5所示:

图5中所示熔覆深度为2 mm，熔覆面积不同(熔覆中心角不同)对轴弯曲量的影响.拟合的方程为

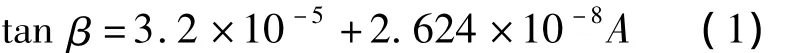
确定出衡量轴弯曲量的tan β后，可以着手根据tan β求出各位置预计熔覆后的轴跳动值.若设轴长为L，在距轴一端长为h的地方进行熔覆，熔覆槽的长度为l，求距离轴端x处的轴跳动值f，推导得出

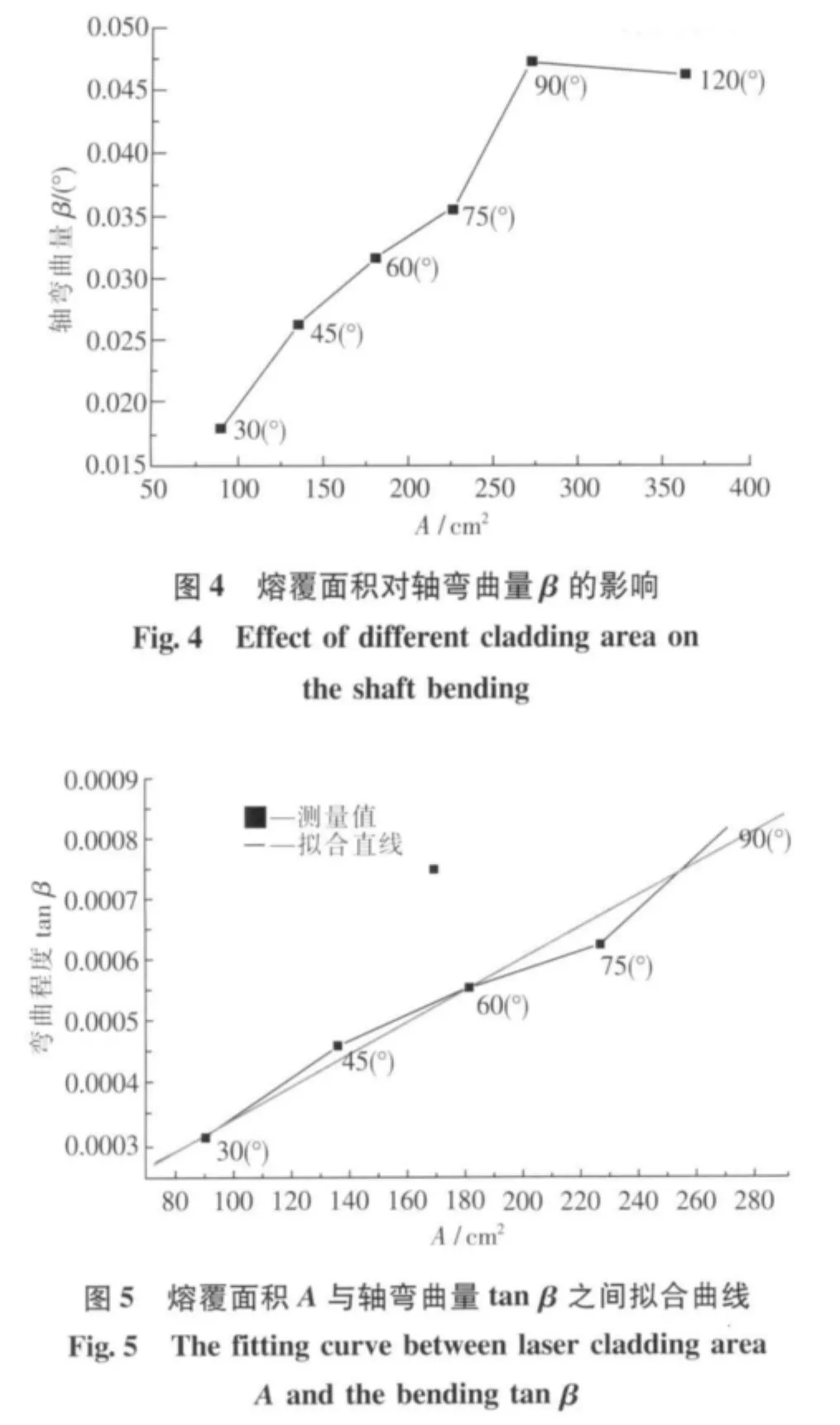
图6 轴跳动值测量值与计算值的比较曲线Fig.6 Eccentricity comparison curves between the measured value and the calculaed value

据上式计算出的跳动值与实测值的比较如图6所示，由图6可知，用公式计算出的跳动值与测量值平均误差为0.001 02 mm，最大误差为0.031 96 mm，因此若已知要校回的跳动值，可以利用这个公式反推回去求得弯曲程度tan β，再由此求出熔覆面积A以及熔覆槽的长度l.

4 结论

(1)轴在激光熔覆后发生了朝向激光束的弯曲变形，当熔覆中心角α小于90(°)时，熔覆面积与最大轴弯曲量成正比关系，熔覆中心角α大于90(°)时，弯曲效果不明显，因此轴类零件激光熔覆校轴时，熔覆中心角α最大取90(°).

(2)抽象出激光熔覆校轴的数学模型，得到轴弯曲量tan β与熔覆面积A之间的关系方程，同时得到不同位置处的轴跳动值关系方程.用公式计算出的跳动值与测量值平均误差为0.001 02 mm，最大误差为0.031 96 mm.说明抽象出的激光熔覆校轴的数学模型正确.

［1］徐滨士，刘世参，史佩京.再制造工程发展及推进产业化中的前沿问题［J］.中国表面工程，2008，21(1):1－5.

(XU Bin－shi，LIU Shi－shen，SHI Pei－jing.The frontier issues of development and industrialization of remanufacturing engineering［J］.China Surface Engineering，2008，21(1):1 －5.)

［2］翟华.轴类零件校直工艺理论研究［D］.合肥:合肥工业大学，2003.

(ZHAI Hua.Research on the shaft straightening technology theory［D］.Hefei:Hefei University of Technology，2003.)

［3］田丰，卢华伦.大型机组汽轮机大抽弯曲原因分析及防弯措施探衬［J］.热力透平，2005，35(2):112－116.

(Tian Feng， Lu Hualun. Cause analysisand technical countermeasures for rotor permanent bending of large steam turbine［J］.Thermal Turbine，2005，35(2):112 － 116.)

［4］李晓薇，张春华，张松，等.激光熔覆技术的研究进展［J］.激光杂志，2007，28(2):1－2.

(LiXiaowei， Zhang Chunhua， Zhang Song， etal.Developments of laser cladding technology ［J］.Laser Journal，2007，28(2):1 －2.)

［5］Geiger M.The mechanisms of laser forming［J］.Ann CRIP，1993，42(1):301－304.

［6］金志广，贾鹏程.火焰加热法矫直大型艉轴的探讨［J］.中国修船，2007，20(2):14－15.

(JIN Zhi－guang，JIA Peng－cheng.Exploration of rectifying rear shaft with flame heating［J］.China Ship Repair，2007，20(2):14 －15.)

Quantitative experimental study on the carbon steel shaft laser cladding bending

ZHENG Hui1，2，HAN Zhi-ren2，CHEN Jiang3，WANG Guo-dong1

(1.State Key Laboratory of Rolling and Automation，Northeastern University，Shenyang 110004，China;2.School of Aerospace Engineering，Shenyang Aerospace University，Shenyang 110136，China;3.Dulu Science and Technology Garden，Shenyang 110136，China)

In order to study the influence of the cladding area on the bending degree，to obtain the mathematic model in shaft laser cladding bending and to derive the empirical formula，the laser cladding test for shaft was designed.The laser cladding test was conducted at the same cladding coat thickness and different cladding coat corresponding center angle，that is cladding area.The results of the experiment show that the shaft is bended facing the laser beam.When the cladding coat corresponding center angle is less than 90(°)，the bending degree is proportional to the cladding area.At the same time，a mathematic model in shaft laser cladding bending was established and the parameter used to measure the degree of the bending was obtained.An empirical formula for the bending degree and the cladding area was established.And an eccentricity formula along the shaft length was derived.The calculated values are much agreeable to the measured ones.The maximal error is 0.032 mm，and the average error is 0.001 mm.It illustrates that the mathematic model is correct and the empirical formula has higher accuracy.

laser technique;shaft straightening;laser cladding;mathematic model;empirical formula

TN 249

A

1671-6620(2011)03-0212-04

2011-06-12.

辽宁省教育厅科学技术研究项目 (L2010428).

郑晖 (1976—)，女，辽宁葫芦岛人，东北大学博士研究生，沈阳航空航天大学副教授;韩志仁 (1964—)，男，河北唐山人，沈阳航空航天大学教授;王国栋 (1942—)，男，辽宁大连人，东北大学教授，博士生导师，中国工程院院士.