双二项风险模型下双险种的破产概率
2011-12-27韩素芳
韩素芳,黄 磊
(1.云南民族大学经济学院昆明650013;2.中兴通讯三亚研究所,海南三亚572000)
双二项风险模型下双险种的破产概率
韩素芳1,黄 磊2
(1.云南民族大学经济学院昆明650013;2.中兴通讯三亚研究所,海南三亚572000)
复合二项模型假定在每一单位时间内索赔或者不发生,或者只发生一次.在经典的复合二项模型中,保险公司按照单位时间常速率收取保费(假定每张保单的保险费相等).但在实际中,不同单位时间所收取的保单数常常不一样,是一个随机变量,可能服从某一离散分布.根据这一实际情况,本文将经典的复合二项风险模型推广,将保单收入过程推广为一个与索赔过程独立的二项过程.这样,盈余过程包含两个二项过程.
风险理论;复合二项模型;索赔;盈余
1 模型定义与实际背景
定义1 设数u≥0,c<0,给定在某完备概率空间(Ω,F,P)上取值于(0,∞)的独立同分布随机变量Xi:i=1,2…以及具有参数P的二项随机序列{N(n)}∞n=0,P∈(0,1),且{Xi:i=1,2…}与N={N(n)}∞n=0独立,令:
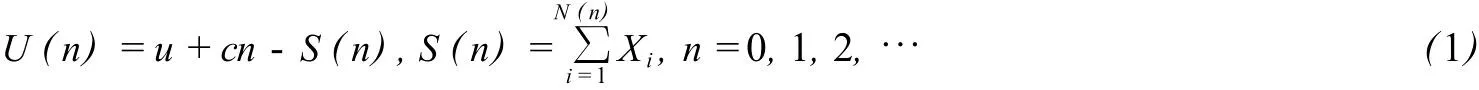
模型的实际背景:在保险公司的事物中,u(u≥0)可以认为是初始资本,c是每单位时间收取的保费,是公司唯一的收入.n是公司的运作时刻,即公司收取保费和进行赔付均在离散时刻n(n=0,1,2…)进行,在完全离散的经典风险模型中,取定一个单位时间a后,可以假定在任意一个时间区间((n-1,a]中,仅可能出现:一方面,或有一个客户投保,或没有客户投保;另一方面,或有一次索赔发生,或没有索赔发生.不失一般性,以下取a=n,即在时间段(n-1,n]中进行的一切工作,我们视为在时刻n进行.投保人发生事故后公司对其进行理赔是公司唯一支出,记第i次赔付量为Xi,则{Xi}∞n=0为取值于R+的独立同分布的随机变量序列.N(n)为到时刻n时止理赔总次数,S(n)为到时刻n为止的总赔付量,则U(n)是公司在时刻n的盈余资本[2].
定义2 本文在定义1的模型的基础上推广定义的模型如下:
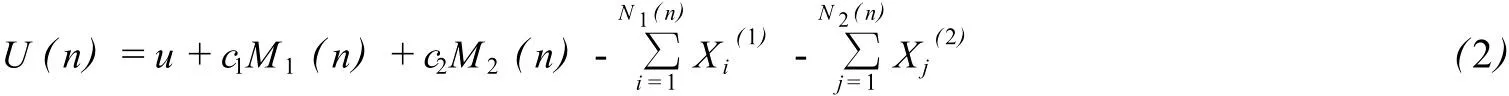
模型说明如下:
①u(u≥0)表示保险公司的初始资本,c1,c2(c1>0,c2>0)分别表示两个险种的保费收取费率;
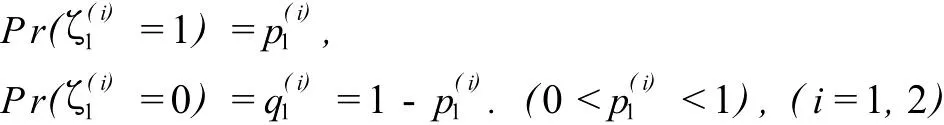

Mi(n)(约定Mi(0)=0)(i=1,2),表示至时刻n时止第i个险种的保费收取次数,(约定Nj(0)=0)(j=1,2)表示至时刻n时止第j个险种所发生的索赔次数.显然{Mi(n);n≥0}是以p1(i)(i=1,2)为参数的二项序列,{Nj(n);n≥0}是以(j=1,2)为参数的二项序列.
③如果在时间区间(n-1,n]内有索赔发生,则在该时间区间内的终端由保险公司支付索赔额,我们以(i=1,2)表示保险公司所支付的第i个险种的索赔额.当取定一钱币单位后,可以假定i=1,2)是取正整数值的随机变量,且…,,…(i=1,2)是独立同分布的随机变量序列.以下假定(i=1,2)与诸(i=1,2)同分布,并称之为第i个险种的个体索赔额.记:μ1=E[X(1)]<∞,μ2=E[X(2)]<∞.每次事故索赔额X(i)(i=1,2)的矩母函数分别为:MX(1)(r)=E[erX(1)],MX(2)(r)=E[erX(2)],r∈(-∞,+∞).
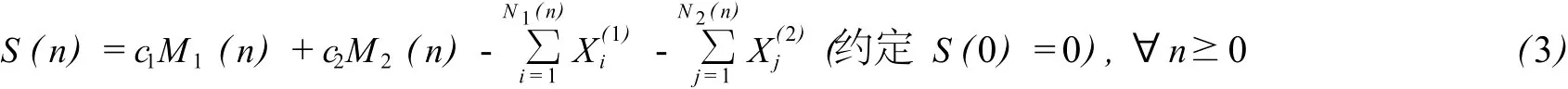
这样,保险公司在时刻n的盈余U(n)可表示为:U(n)=u+S(n),n=0,1,2,….为了保证保险公司的稳定经营,假定E[Sn]>0,即:

(iii)若θ=0,则因此在θ<0和θ=0的情况下,保险公司必破产,故只考虑θ>0的情形.而破产时刻,最终破产概率分别定义为:τ=inf{U(n)<0,n≥1},Ψ(u)=P{τ<∞|U(0)=u}为了强调对u的依赖关系,我们有时选用记号Pu{·}=P{·|u(0)=u}.
2 主要结果
引理1 盈余过程{S(n);n=0,1,2,…}有下列性质:
(1)S(0)=0;
(2)具有平稳独立增量;
(4)存在正数r,使得E[e-rS(n)]<∞.
引理2 对于盈余过程{S(n);n=0,1,2,…},存在函数g(r),使得E[e-rS(n)]=eng(r)
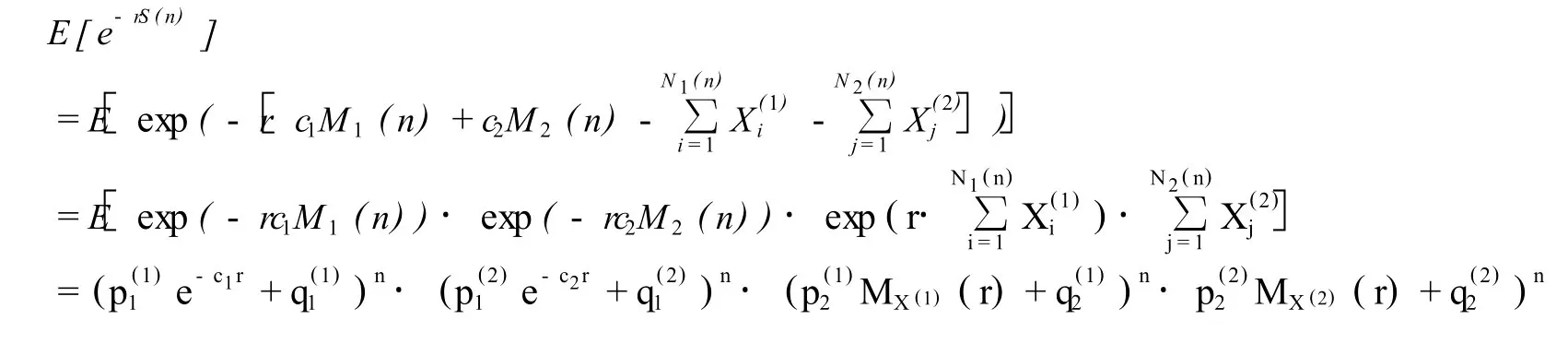
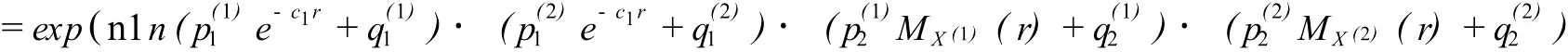
故:g(r)
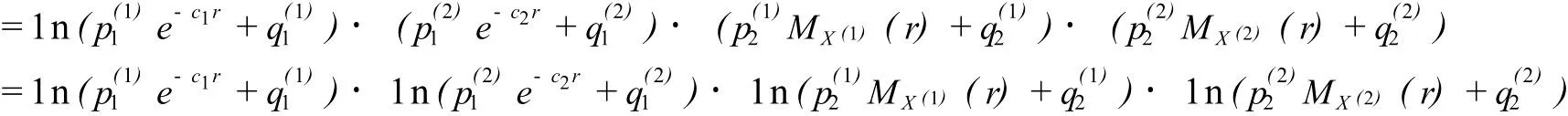
引理3 方程g(r)=0存在唯一的正根R,称为调节系数.

(5)式第一项的分子为:
(5)式第三项的分子为:
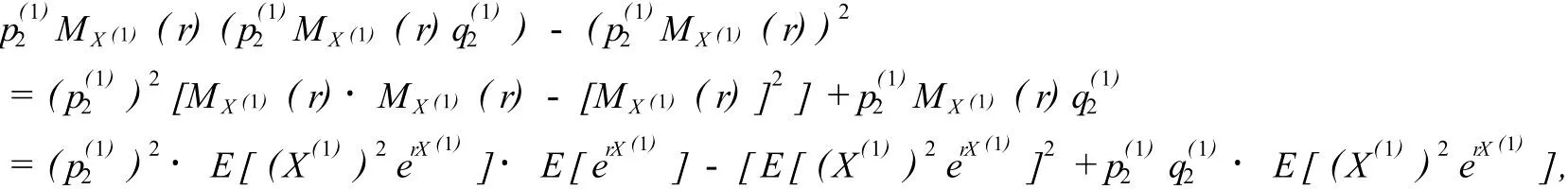
由施瓦兹(Schwarz)不等式知:E[(X(1))2erX(1)]·E[erX(1)]-E[(X(1))erX(1)]2≥0,因此上式≥[(X(1))2erX(1)]>0.而第三项的分母显然大于0,故第三项大于0.同理可证第四项也大于0.
综上即得:g(r)>0,故曲线g(r)在r>0是下凹的,所以r只要取足够大的值,一阶导数g(r)将保持为正,从而g(r)在r>0内有唯一极小值点,记之为R.
定理1 对于盈利过程{S(n);n=0,1,2,…},定义事件流FS={;t=0,1,2,…},其中=σ{S(n);n≤t=0,1…}是鞅.
证明:对任意的s≤t,由引理2得:

定理2 在风险过程{U(n);n=0,1,2,…},其最终破产概率为节系数.特别的,Ψ(u)≤e-Ru∀u≥0.
证明:由

而:E[e-rU(n)]=e-ru·E[e-rU(n)]=e-ru·eng(r)
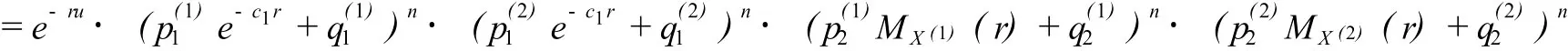
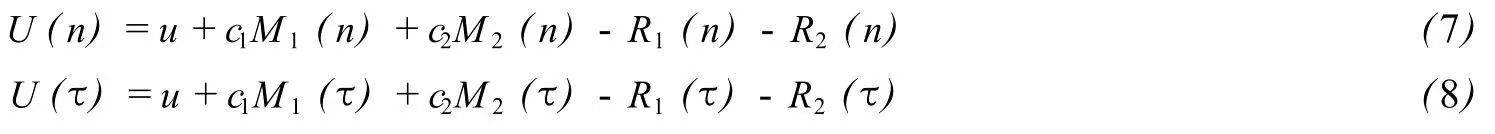
(7)-(8)得:
U(n)=U(τ)+c1(M1(n)-M1(τ))+c2(M2(n)M2(τ))-(R1(n)-R1(τ))-(R2(n)-R2(τ))
对于给定的τ,R1(n)-R1(τ),R2(n)-R2(τ)与U(τ)独立,且分别服从参数为:n-r和,n-r和的复合二项分布,从而:

根据引理3,选取r=R得:E[e-rU(τ)|τ<n]·Pu{τ<n},且此时(6)式可化简为:

令:n→∞,则(9)式右端第一项变为:E[e-rU(τ)|τ<∞]·Pu{τ<∞}.
因此如果能够证明当n→∞时,(9)式右端第二项趋于0,那么定理即得证.证明如下:
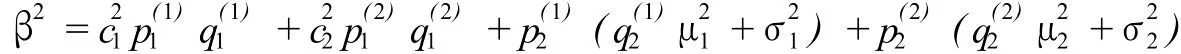
易知:

令:Λ≡u+na+βn2/3,由于a>0,故只要n充分大,Λ就是正的,而且当n→+∞时,Λ→+∞.
现将(9)式右端第二项用u(n)与∧的大小拆成两项,即得:E[e-R·U(τ)|τ≥n]·Pu{τ≥n}

由车贝晓夫(Chebychev)不等式得:
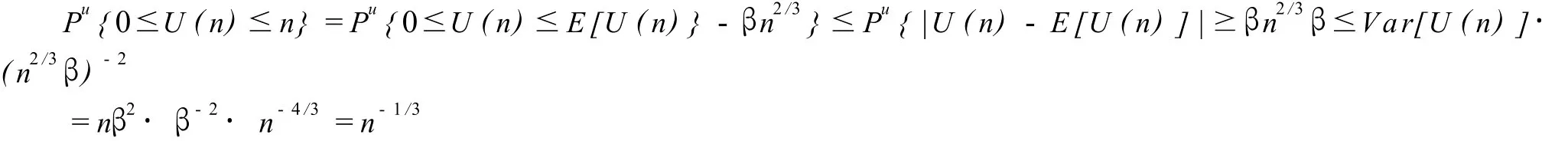
故当n→+∞时,n-1/3→0,且当n→+∞时,Λ→+∞,因此e-RΛ→0,综合以上两点即得:当n→+∞时,(10)式右端趋进于0.
再因,在{τ<+∞}上,-R·U(τ)≥0,即得:Ψ(u)≤e-Ru,∀u≥0.定理证毕.
[1]W illmot G E.Ruin probability in the compound binomial process[J].Insurance:Mathematics and Economics,1993,12:133-142.
[2]赵飞,王汉兴.双二项风险模型的破产概率[J].应用数学与计算数学学报,2004,18(2):73-78.
[3]龚日朝,杨向群.复合二项风险模型下的破产概率[J].吉首大学学报(自然科学版),2000,21(4):41-43.
[4]徐金福,刘再明.广义复合二项风险模型下的破产概率[J].数学理论与应用,2004,24(1):93-96.
[5]张茂军,南江霞.保费随机的复合二项风险模型的破产概率[J].科技通报,2005,21(3):367-371.
Ruin Probability of a Double Binomial Risk Model with Two-type Claims
HAN Su-fang1,HUANG Lei2
(1.School of Economics,Yunnan University of nationalities,Kunming 650013,China;2.Zte Sanya institute,Sanya 572000,China)
Compound binomial model assumes that the claim either not occur,or only occurs once each unit of time.In the classical compound binomial model,insurance companies often charge premium rates according to constant rate each unit of time(assuming the same premium perwarranty).However,in practice,the number of warranty charged in different units of time is of ten not the same,it is a random variable,it may be obey discrete distribution.According to the actual situation,this thesis will expand classical compound binomial risk model.the process of the warranty income was expanded to be a binomial process that is independent from a claims process.In this way,the surplus process consists of two processes.
Risk Theory;Compound binomial model;claims;surplus
O29
A
1008-9128(2011)02-0018-05
2010-12-02
国家“973”基金项目(2006CB100206);云南省“十一五”科技重点攻关项目(2010NG0011)
韩素芳(1982-),女,山东济宁人,硕士。研究方向:复杂网络及数理金融。
[责任编辑 张灿邦]
