表面声阻抗近似局域k-k关系的实验研究
2011-12-27张青友和万全
闵 琦,张青友,和万全
(红河学院理学院云南蒙自661100)
表面声阻抗近似局域k-k关系的实验研究
闵 琦,张青友,和万全
(红河学院理学院云南蒙自661100)
利用石棉多孔材料对表面声阻抗近似局域k-k关系进行了实验研究,通过最小频率分辨率分别为0.25Hz、0.5Hz和1Hz的理论和实验值的对比研究发现理论值与实验值相互吻合,从实验上很好地验证了表面声阻抗近似局域k-k关系的正确性.
石棉;表面声阻抗;近似局域k-k关系
引言
k-k关系是上世纪二十年代由H.A.Kramers和R.Kronig分别独立创立的,它是自然界中线性系统因果律的严格数学表述,k-k关系自创立以来在光学、高能粒子物理等领域得到了广泛的研究和应用[1-4].k-k关系在声学领域的研究和应用始于上世纪六十年代,但直到近十年来才有较多的成果出现,这些成果主要集中在媒质中声速与衰减的关系上,有关声阻抗尤其是局域声阻抗k-k关系的研究仍然不多见[5-7].文献[8]针对多孔材料表面声阻抗的理论模型及其因果律进行了研究,并给出了表面声阻抗近似局域k-k关系式,但至今仍未有实验对其进行过验证.为此,本文选用常见的防火吸声材料石棉为实验材料对这一近似局域k-k关系进行实验研究,以验证这一近似局域关系的正确性.
1 表面声阻抗k-k关系
置于声场中的材料如果表面复声压为p、由声场引起的材料表面质点复速度的垂直分量为v,则材料表面声阻抗可定义为[9]

其中,w为角频率,实部R(w)、虚部X(w)分别为材料表面声阻和声抗.归一化的表面声阻抗为
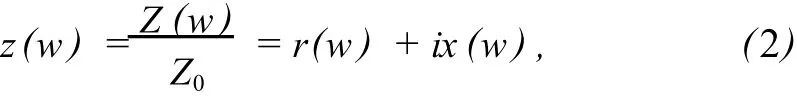
这里,Z0为空气特性阻抗.如果阻和抗的相互响应是线性响应,取w为复数,由表面阻抗Z(w)的物理性质不难证明Z(w)在w张成的上半复平面上处处解析,而且当w→∞时,Z(w)一致地→0,从而R(w)、X(w)满足希尔伯特变换(Hilbert transfo rm s)的条件,成为希尔伯特变换对[4,10],即

当改变正负号时,由物理性质可知

这里“*”表示共轭.(3)、(4)式可进一步写成

上两式即是材料表面声阻抗k-k关系.从这对k-k关系式可以看出阻和抗并不是相互独立的,而是可以相互确定,但要做到这一点必须知道阻或抗在全频域上的信息,所以称这对关系式为表面声阻抗非局域k-k关系.遗憾的是,在实际中要知道阻或抗在全频域上的信息是很难办到的.鉴于此,研究声阻抗局域k-k关系成为了非常具有实际意义的工作.在阻R(w)、抗X(w)相互关系为线性响应且随频率w的增加不做激烈变化的情形下,略去高阶项,可求导出材料表面声阻抗近似局域k-k关系[6,8]

从而可得到归一化后的表面声阻抗近似局域kk关系为
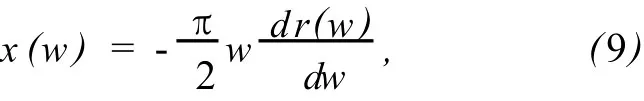
与阻抗非局域k-k关系不同,理论上声阻抗局域k-k关系可以通过频域上任意一区域的阻求出该区域对应的抗,从而使其具有了很强的实用性,接下来将通过石棉多孔材料的实验对其予以验证.
2 表面声阻抗局域k-k关系的实验验证
2.1 实验系统及原理
实验测量方法参照GB/T18696.2-2002标准即阻抗管中吸声系数和声阻抗的测量.实验系统如图1所示,传声器采用1/4英寸B&K4944,前置放大器为B&K2670;声源采用M cCauley6520扬声器;功放采用国产GF-10型功率放大器;数据采集与分析系统采用目前较为先进的B&K Pulse3560C多通道分析仪.
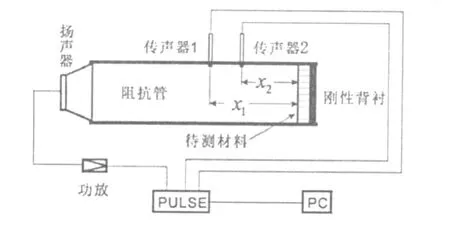
图1 表面阻抗测量系统
如果取待测材料表面为参考面,则待测材料表面声场可分解为入射声场和反射声场Pr分别为待测材料表面处的入射声场和反射声场的声压幅值,k0=ω/c0为复波数,c0为声速.此时,传声器1、2处的声压分别为P1=为材料表面至传声器1中心的距离,x2为至传声器2中心的距离.传递函数定义为

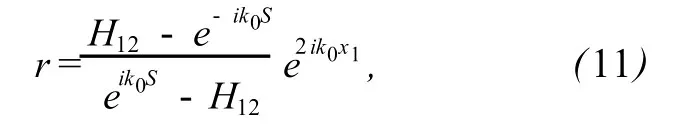
式中s=x1-x2.通过r即可求出归一化表面声阻抗为,具体求解公式为

z的实部和虚部即分别为表面归一化声阻r(w)和声抗x(w).B&K Pulse3560C多通道分析仪自身能够直接测量出传递函数H12,所以当试验测得传递函数H12的值后即可通过(11)、(12)式求得归一化表面声阻抗实验值.
实验选用的材料是用石棉压实而成的多孔材料,为能放入阻抗管中进行实验测量,石棉多孔材料已被事先切割成圆块状,其直径为2.9厘米,厚度为1.8厘米.实物如图2所示

图2 石棉多孔材料
2.2 实验结果
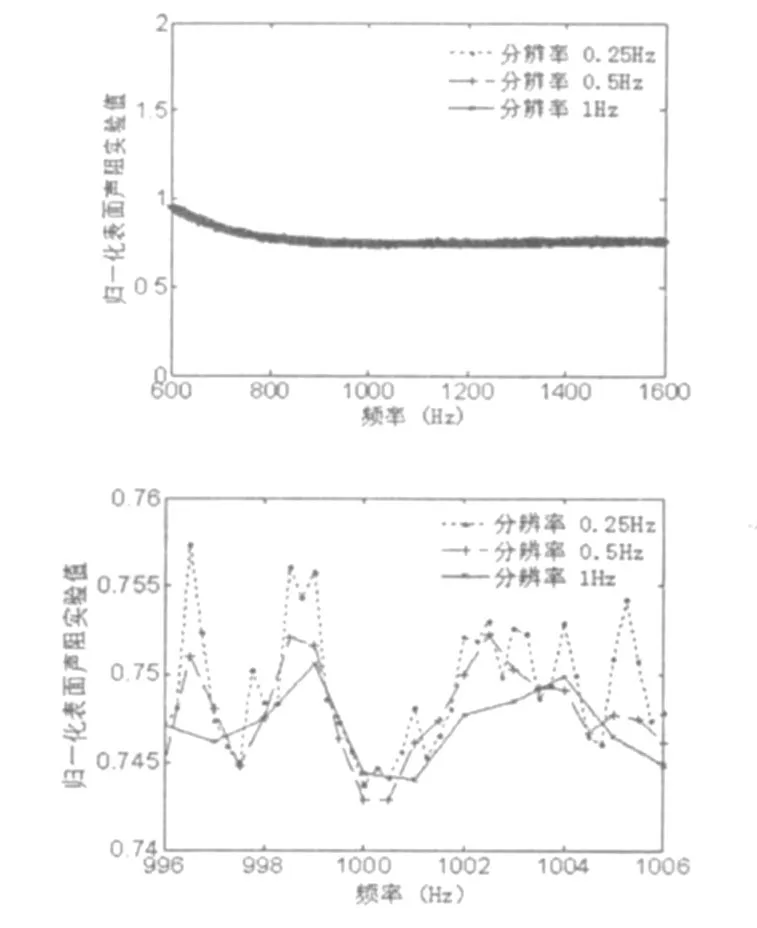
图3 石棉多孔材料不同频率分辨率下的表面声阻实验值(a)600~1600Hz范围内,(b)1000Hz附近.
实验测量时将Pulse的测量线数固定在最大值6400,频率测量范围依次选择其固有的1600Hz、3200Hz及6400Hz三档,此时得到最小频率分辨率分别是0.25Hz、0.5Hz和1Hz.考虑到三个测量档位的频率覆盖范围,为对比分析不同频率分辨率下的实验结果,除各测量档位都能覆盖的600Hz~1600Hz频率范围外,还将选择1000Hz附近作为进一步对比的频率区域.实验测得的石棉多孔材料表面声阻抗如图3、图4所示.由图3a和图4a可以看出在不同最小频率分辨率下的实验测量值一致性非常好,测量值均主要分布在很窄的值域内;但同时由1000Hz附近局部放大的图3b和图4b可以清楚地看出,由于实验得到的测量值是在设定的最小频率分辨率下的平均值,随着最小频率分辨率的粗粒化,实验测量值在频域上被平均得越厉害,实验值在频域上的细部起伏就越少,从而测量丢失的信息就越多.最小频率分辨率为0.25Hz时能够测量得到的阻、抗在频域上的细部起伏信息经过最小频率分辨率0.5Hz后,在最小频率分辨率为1Hz时已经被丢失许多,阻、抗曲线都已变得平滑许多.

图4 石棉多孔材料不同频率分辨率下的表面声抗实验值(a)600~1600Hz范围,(b)1000Hz附近
为验证表面声阻抗近似局域k-k关系(9)式的正确性,根据(9)式,利用实验测量得到的表面声阻r(w)采用差分求导的方法求取归一化的表面声抗理论值xc(f),具体求解声抗理论值xc(f)的差分式为
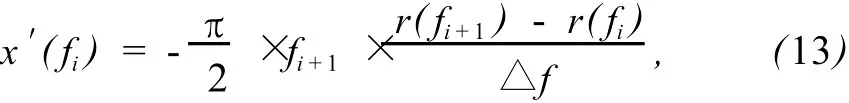
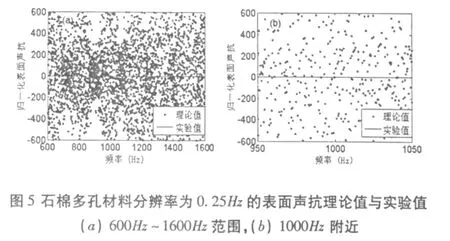
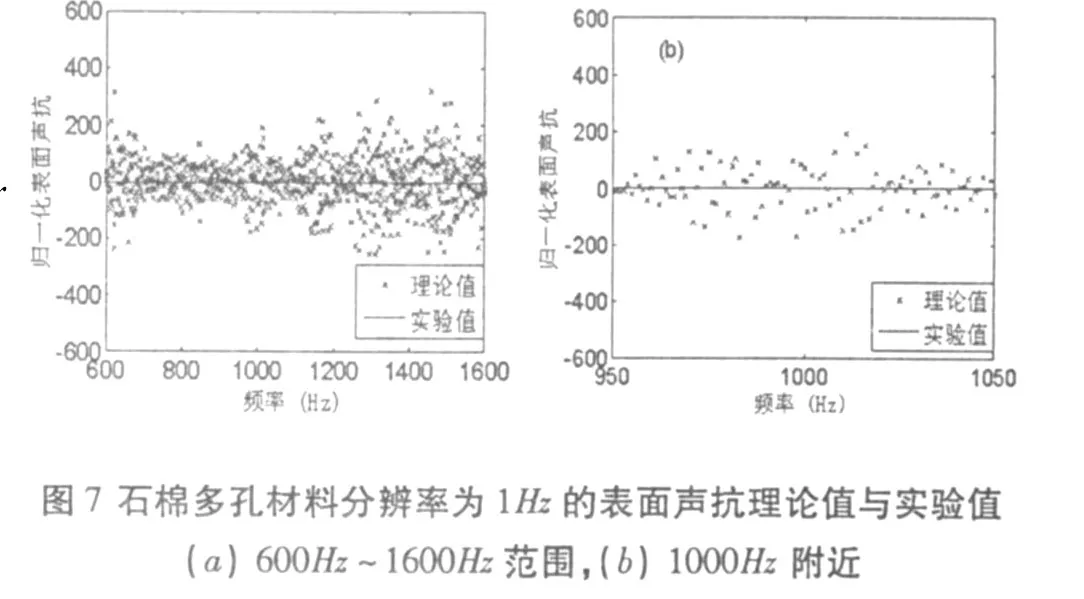
其中,fi为频率,△f=fi+1-fi即是相应的最小频率分辨率,i=1,2,…,6400.由此计算得出的不同最小频率分辨率下的归一化表面声抗的理论值与实验测量值的分布情况分别见图5~7.
从图5~7可以清楚地看出最小频率分辨率从0.25Hz经过0.5Hz到1Hz不断粗粒化的过程中,根据近似局域k-k关系(9)式由阻的实验值求取的材料表面声抗的理论值都能很好地对称分布在实验值的上下两边,从而由实验很好地验证了近似局域k-k关系(9)的正确性.这里值得注意的是,随着最小频率分辨率不断的粗粒化,抗的理论值的分布区域越靠近实验值.之所以如此,如前所述,是因为随着最小频率分辨率的粗粒化测量丢失越来越多的信息,阻的实验测量值曲线变得越来越平滑,加之最小频率分辨率的粗粒化使得由差分近似求解抗的理论值时差分式对的抗的理论值的平均作用越大,从而最终造成抗的理论值随着最小频率分辨率的粗粒化分布区域逐渐收缩变窄.

3 结论与讨论
本文采用石棉多孔材料对表面声阻抗局域k-k关系进行了实验研究,分别通过最小频率分辨率0.25Hz、0.5Hz、1Hz下的理论和实验值的对比研究发现理论值与实验值相符,很好地从实验上验证了表面声阻抗近似局域k-k关系的正确性,由此也说明了石棉多孔材料表面声阻抗之间的响应满足线性条件下的因果律.但同时也可看到,由于声阻抗近似局域kk关系式(8)和(9)略去了高价项,加之目前实验系统的关键组成部分即数据采集与分析系统Pulse3560C存在最小频率分辨率极限,最小的频率分辨率在实验中只能达到0.25Hz,实验测量仍然不够精细,丢失过多信息,这一最小频率分辨率对于求解理论值的差分式显得还太粗,从而造成理论值的发布区域仍然较广,使得目前与利用近似局域k-k关系由局域阻和抗相互求取的实际应用还存在一定距离.
[1]KronigL R.On the theory of dispersion of X-rays[J].J.Opt.Soc.Am.,1926;12(6):547-557.
[2]Nussenzweig H M.Causality and Dispersion Relations[M].New York:Academic press,1972.
[3]Peiponen K E,Saarinen J J.Generalized Kramers-Kronig relations in nonlinear optical-and THz-spectroscopy[J].Rep.Prog.Phys.,2009;72:1-19.
[4]闵琦,王世恩.Harmonic oscillator,causality and Hilbert transform pair[J].红河学院学报,2010;7(2):1-4.
[5]Mangulis V.Kramers-Kronig or dispersion relations in acoustics[J].J.Acoust.Soc.Am.,1964;36(1):211-212.
[6]O’DonnellM,Jaynes E T and Miller J G.Kramers-Kronig between ultrasonic attenuation and phase velocity[J].J.Acoust.Soc.Am.,1981;69(3):696-701.
[7]Waters K R,Mobley J,Miller J G.Causality-imposed(Kramers-Kronig)relationships between attenuation and dispersion[J].IEEE,2005;52(5):822-833.
[8]Berthelot Y H.Surface acoustic impedance and causality[J].J.Acoust.Soc.Am.,2001;109(4):1736-739.
[9]Morse P M,Feshbach H.Methods of Theoretical Physics[M].New York:McGraw-Hill,1953,372-373.
[10]Bracewell R N.The Fourier Transform and itsApplications,2nd ed[M].New York:McGraw-Hill,1986,359-365.
Experimental Investigation in the Local k-k Approximation of Surface Acoustic Impedance
MIN Qi,ZHANG Qing-you,HE Wan-quan
(Department of Physics,Hong he University,Mengzi 661100,China)
With porous asbestos material,an experimental investigation in the local k-k approximation of surface acoustic impedance is carried out.It is found that the theory agrees with experimental results under the different frequency resolution 0.25Hz,0.5Hz and 1Hz,which confirms experimentally the local k-k approximation of surface acoustic impedance.
asbestos;surface acoustic impedance;local k-k approximation
O424
A
1008-9128(2011)02-0001-04
2011-03-06
国家自然科学基金项目(10574135);云南省教育厅科学研究基金项目(5Y0040A);红河学院校级科研项目(XJ IY0514).
闵琦(1972一),男,云南人,博士,副教授.研究方向:物理声学及理论物理.
[责任编辑 张灿邦]
