关于各向异性电介质圆柱形电容器的讨论

宋纳红，王玉生

(1.河南财经政法大学计算机与信息工程学院，河南郑州450002;

2.华北水利水电学院数学与信息科学学院，河南郑州 450011)

关于各向异性电介质圆柱形电容器的讨论

宋纳红1，王玉生2

(1.河南财经政法大学计算机与信息工程学院，河南郑州450002;

2.华北水利水电学院数学与信息科学学院，河南郑州 450011)

利用电容器的并联、串联以及能量的方法，计算了充有线性各向异性电介质和对数各向异性电介质时圆柱形电容器的电容，并比较了两种电介质对电容的影响.

圆柱形电容器;电容;各向异性电介质

电容器作为能量存储器件，由于其能量密度高、使用寿命长、免维修、对环境无污染等优点得到了广泛关注［1－3］，同时电容器在电路中也起着举足轻重的作用，安装在电网中的各级变电站和线路上可以补偿电力系统的无功功率，减少系统电能损耗，提高功率因数，从而提高电能质量.

电容是电容器的重要参数，根据不同需要，电容器的形状以及电容器内所填充的电介质也不同.圆柱形电容器是最常见的电容器，对于真空和各向同性电介质的情况已经有很多讨论，并且可以精确求出其电容［4－5］.而各向异性电介质电容讨论较少，其电容一般通过实验的方法测量.如果能够从理论上计算出各向异性电介质的电容，就能在电容器的设计应用中给以重要指导.本文根据电容器的串联和并联知识以及电场能量与电容的关系，讨论了圆柱形电容器充有线性和对数各向异性电介质时的电容，并得出了其电容和真空时电容的关系［6］.

1 各向同性圆柱形电容器电容

假设圆柱形电容器高度为L，内外半径分别为R1和R2，如图1所示.设两个极板带电分别为+Q、－Q，由高斯定理可先求出电场强度，然后根据电容器电容的定义可得［5］

其中e为各向同性电介质的电容率.

在复杂电路中，为了满足需要往往把多个电容器串联或并联.当有多个电容器并联时，总电容为

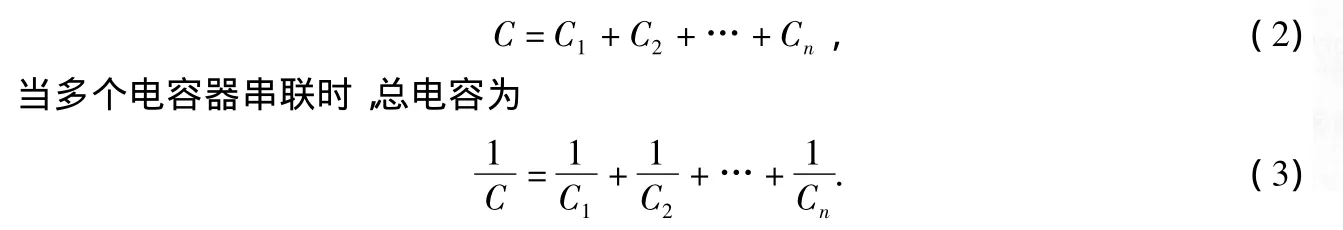
图1 圆柱形电容器Fig.1Cylindrical capacitors

2 线性各向异性电介质圆柱形电容器的电容

2.1e=e0(1+kx)时

如果在电容器极板间充有电容率为e=e0(1+kx)的线性各向异性电介质，电容器的电容可以按下面的方法计算.如图2所示，在x处取一个高度为dx的圆柱为微元，整个电容器可以看做很多个高度为dx的圆柱形电容器并联而成.由(1)式得出微元的电容可表示为可见圆柱形电容器充有线性各向异性电介质时，总电容与电容器的高度和电介质的电容率有关.若k=，则C=1.5C0，充有此种电介质的电容是真空电容器的1.5倍.

2.2e=e0kr时

当电介质的电容率为e=e0kr时，其中r为距离圆柱形电容器轴线的距离.可以用两种方法来求解电容器的电容.

2.2.1电容器串联法

如图3所示，在电容器内部取一个半径为r厚度为dr的圆柱体为微元，整个电容器可以看做是由很多个高度为dr的电容器串联而成.微元电容器的电容为

图2 圆柱形电容器并联示意图Fig.2Cylindrical capacitors connected in parallel

2.2.2能量法

除了用电容器串联方法求解电容，还可以用电容器能量与电容的关系来求解电容.首先，根据有介质时的高斯定理求出圆柱体内部的电位移矢量D=，l为单位长度电容器极板所带电量，然后，根据电位移与电场强度的关系可求出电场强度

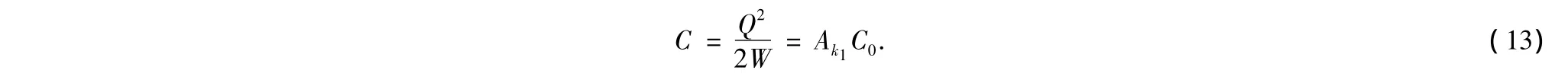
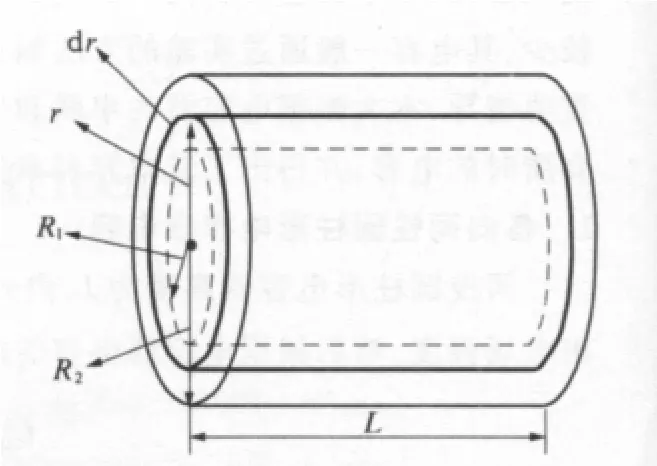
图3 圆柱形电容器串联示意图Fig.3Cylindrical capacitors connected series

用电容器串联法和能量法均可求出电容器的电容，充有此种电介质的圆柱形电容器的电容是真空电容器电容的Ak1倍，Ak1与介质的电容率以及电容器的大小形状有关.

3 对数各向异性电介质圆柱形电容器的电容

3.1e=e0［1+ln(1+kx)］时

当电容器充有电容率为e=e0［1+ln(1+kx)］的电介质时，与线性电介质情况类似，选取高度为dx的圆柱为微元，则微元的电容为充有此种电介质的圆柱形电容器电容是真空时的1.4倍，所以，轴向对数各向异性电介质比线性各向异性电介质对电容器电容的影响小.

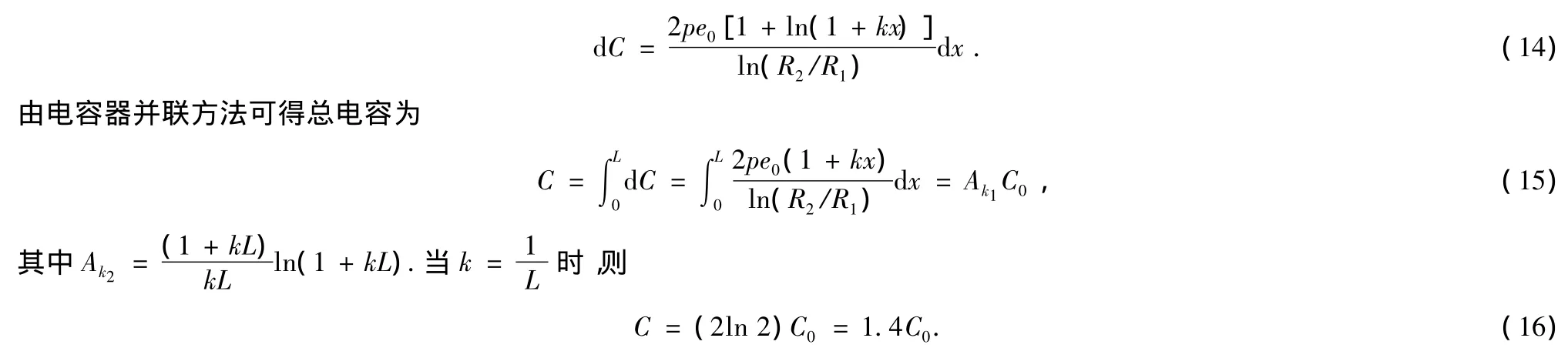
3.2e=e0ln(kr)时

4 结论

根据各向同性电介质的串联和并联知识以及电容器能量和电容的关系，计算并讨论了各向异性线性电介质、对数电介质对圆柱形电容器电容的影响.结果表明，本文讨论的两类电介质对电容都有一定的影响，沿轴向填充的线性和对数各向异性电介质分别使电容增加为真空的1.5倍和1.4倍.沿径向填充的两类电介质使电容变为真空时的Ak2和Ak3倍.

［1］OKAJIMA K，OHTA K，SUDOH M.Capacitance behavior of activated carbon fibers with oxygen-plasma treatment［J］.Electrochimica Acta，2005，50(11):2227－2231.

［2］ZOU Xiao，FANG Guojia，YUAN Longyuan，et al.Improved electrical characteristics and reliability of amorphous InGaZnO metal-insulator-semiconductor capacitor with high k HfOxNy gate dielectric［J］.Microelectronics Reliability，2010，50(7):954–958.

［3］HONDA K，TATA N R，TRYK D A，et al.Electrochemical characterization of the nanoporous honeycomb diamond electrode as an electrical double-layer capacitor［J］.Journal of the Electrochemical Society，2000，147(2)659－664.

［4］王利敏.非平行板电容器电容的又一计算［J］.大学物理，2006，25(4):23－24.

［5］马文蔚，周雨青，解希顺.物理学教程［M］.2版.北京:高等教育出版社，2006.

［6］吴百诗.大学物理基础［M］.北京:科学出版社，2007.

Discussion on Cylindrical Capacitor Filled with Anisotropy Dielectric

SONG Na-hong1，WANG Yu-sheng2

(1.College of Computer and Information Engineering，Henan University of Economics and Law，Zhengzhou450002，China; 2.College of Mathematics and Information Sciences，North China University of Water Resources and Electric Power，Zhengzhou450011，China)

Using the principles of capacitors connected in parallel and in series and the method of electrical energy，the capacitances of cylindrical capacitor filled with linear anisotropy dielectric and logarithmic anisotropy dielectric are calculated.The impacts of two kinds of dielectric to capacitor are compared.

cylindrical capacitor;capacitance;anisotropy dielectric

O441.1

A

1007－0834(2011)04－0029－03

10.3969/j.issn.1007－0834.2011.04.010

2011－07－28

华北水利水电学院青年科研基金项目(HSQJ2009018)

宋纳红(1978—)，女，河南平顶山人，河南财经政法大学计算机与信息工程学院讲师.