一种动态绘制无交叉法线坡面线的新算法

方 雷，刘仁义，吕 干，杜震洪，姚申君

1.浙江大学浙江省资源与环境重点实验室，浙江杭州310028；2.浙江大学地理信息科学研究所，浙江杭州310027；3.香港大学地理系，香港999077

一种动态绘制无交叉法线坡面线的新算法

方 雷1，2，刘仁义2，吕 干1，2，杜震洪1，2，姚申君3

1.浙江大学浙江省资源与环境重点实验室，浙江杭州310028；2.浙江大学地理信息科学研究所，浙江杭州310027；3.香港大学地理系，香港999077

研究一种动态绘制任何形状的无交叉法线坡面线的新算法，用以克服传统手工绘制复杂坡面线及原有自动化技术的不足。并证明基于“实交点定理”及其“补充定理”的算法是生成无交叉坡面线的充分条件。进一步说明使用该算法可以动态绘制地形图所需要的任何形状的法线自然（加固）斜坡、崩崖、陡崖、陡石山、堤岸等图式符号。最后，通过三组试验验证算法的有效性，分析算法的特点及影响因素。

斜坡；填充图案；制图；地理信息系统

1 引 言

《地形图图式》［1］（GB／T 7929—1995）规定：斜坡指各种天然形成和人工修筑的坡度在70°以下的坡面地段。其样式如图1所示，符号的上沿实线表示斜坡的上棱线，长短线表示坡面。符号的长线一般绘至坡脚，当坡面较宽且有明显坡脚线时，可测绘坡脚线，以范围线（点线）表示。计算机自动制图软件中斜坡符号的一般画法：确定上棱线和坡脚线后绘制一组自上棱线开始指向坡脚线的长短相间的坡面线。坡面长短线有两种画法：等分法和法线法（图1（a）和图1（b））。其中法线法是将上棱线按固定长度等分，由各等分点出发分别向坡脚线做一组法线段（与上棱线垂直）生成坡面线的方法。通过该方法得到的坡面长短线称为法线坡面长短线或法线坡面线，得到的斜坡称为法线（加固）斜坡。由于上棱线段间的夹角、坡面线的间隔和长度三个因素的影响，法线法的坡面长线在填充坡面过程中会出现彼此交叉现象，使得法线法生成的坡面线非常杂乱（图1（c）），因此使用法线法生成美观的无交叉坡面长线算法是本文的主要研究内容（图1（d））。

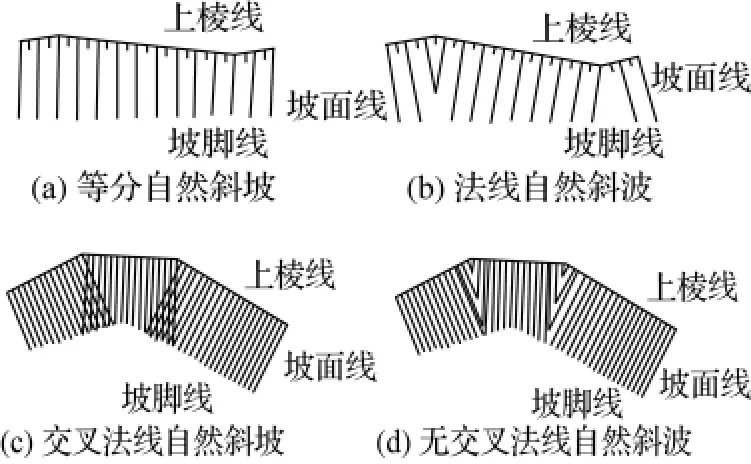
图1 自然斜坡线Fig.1 Natural slope lines

若将上棱线、坡脚线及其两端边缘的两条坡面线看成是一个封闭的简单多边形，那么坡面线的生成则转化成一个多边形的填充图案或者填充符号生成问题。平行线或交叉线等规则填充图案的生成算法较成熟，多数流行的GIS软件可以符号化“等长”的坡面长短线（即便存在交叉情况）。但是，法线坡面线具有特殊性：① 斜坡上棱线的重要性远远大于坡脚线；② 坡面线均从上棱线出发绘至坡脚线，具有指向性；③ 坡面线根据上棱线与坡脚线的相对位置、长度和角度动态生成，无法提前定制；④ 坡面线在上棱线附近均为等间距的法线段，若不进行截取操作会在坡脚线附近大量交叉，破坏填充图案的美观性。而计算机图形学专家往往将多边形区域填充的研究重点集中在实现规则图案的填充算法上［2－3］；制图学专家的研究则将研究重点集中在GIS空间数据与地形图图式一体化的模型研究上［4－5］，符号或符号库的合理设计和建立［6］，符号化效率［7－8］，随时间变化的动态符号生成［9］，颜色、线条等组合方法对符号进行表达［10］等方面；文献［11］甚至提出三维陡崖的自动建模方法。而少有学者系统地研究类似坡面线这类具有上述四个特点的图式符号动态生成方法。一些测绘制图软件（如南方CASS6.1）或使用人机交互方式，或使用自动方式从技术上解决部分法线斜坡坡面线的交叉问题，但也仅限于形状较规则的法线斜坡，对于是否适用于所有形状坡面线的填充并未证明。本文在文献［12］的基础上提出一种基于实交点定理及其补充定理的动态绘制任何形状斜坡的无交叉坡面线算法较好地解决这一问题。

2 算法介绍

形成无交叉坡面线的基本方法是裁剪法线段交叉部分，其关键是求出恰当的交点并裁剪掉交点至坡脚线的多余法线段。在同一平面内，n（n为正整数）条直线最多可能有个交点，该情况下选择出恰当的交点非常困难。为此提出基于实交点定理及其补充定理算法（algorithm based on real intersection and complementary theorem，ABRICT）。本节首先明确算法的四个前提假设及相关概念，在分析CASS算法缺陷的基础上提出实交点定理及补充定理，最后描述完整的ABRICT算法的实现步骤。

2.1 前提假设

研究对象为《地形图图式》［1］中斜坡图式，算法和证明过程基于以下四条前提假设：① 由斜坡上棱线、坡脚线及坡面边缘线组成的多边形是非自相交多边形；②坡面线不通过上棱线的节点，若坡面线自动生成过程中刚好通过上棱线节点，则可将其向节点一侧进行微小平移等价替换；③ 坡面线均与坡脚线同侧；④ 斜坡上棱线单侧生成坡面线，若出现两条坡脚线在一条上棱线两侧的情况，则可用两条上棱线和两条坡脚线等价替换。

2.2 算法相关定义描述

整体整洁、无交叉、疏密程度均衡的坡面线称为无交叉坡面线。即由上棱线和两条坡面线组成的封闭多边形内部不包含这样的线段，穿越封闭多边形到达坡脚或者在多边形外部与其他坡面线相交。如图2中法线段3、5和上棱线构成的封闭多边形不满足上述定义。

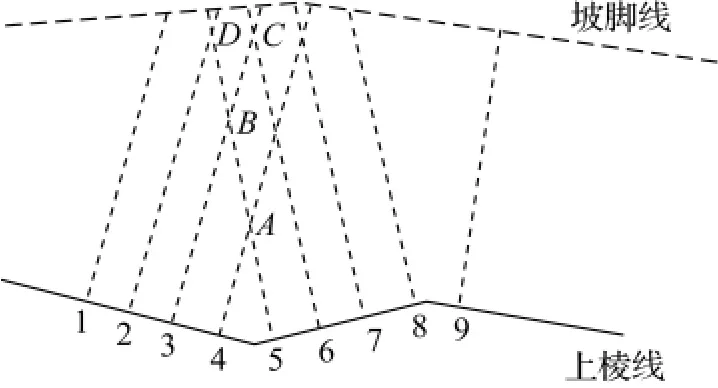
图2 算法相关定义说明图Fig.2 Illustrations of terms in relation with the algorithm

生成无交叉坡面线算法的关键是求出恰当的交点并裁剪掉交点至坡脚线的多余法线段。然而，并不是所有的交点都要作裁剪多余线段的处理（如图2中D点，法线段5在D点之前已与法线段4有交点A，所以D点实际上落在法线段5的多余线段上，该点无须做裁剪多余线段处理）。此类落在法线段的多余线段上，且又不做裁剪多余线段处理的交点为虚交点；需要做裁剪多余线段处理的交点称为实交点。若两条相交法线在相交之前均不与其他法线段相交，则称其交点为初始实交点（如图2中A点）。如果两条相交法线在相交之前已与其他法线段的多余线段相交，则称其交点为事实实交点（如图2中C点）。此外，称依次交于实交点的法线段为对称法线段，并称经过交叉部分裁剪处理的坡面线与上棱线组成的封闭多边形为法线多边形。

2.3 实交点定理及其缺陷

2.3.1 CASS算法及其缺陷

实交点的定义提供了寻找实交点的方法。由于确定初始实交点的位置更为重要，寻找第一对相交法线段便成为解决问题的关键。CASS算法是诸多寻找实交点的算法中应用最广的一个。它可描述为：自左向右（或自右向左）遍历法线段，将第一对相交法线段的交点作为初始实交点，并进行裁剪处理；然后将处理后的法线段内侧的相邻法线段的交点作为事实实交点，再进行裁剪处理，直到不再存在相交法线段为止。使用CASS算法生成的无交叉法线自然斜坡图式如图3所示。但是，该算法并不能对所有形状的斜坡完成坡面区域的“美观填充”。法线坡面线的美观之处在于其沿上棱线夹角角平分线呈现一种对称性。图3（a）中斜坡图式AB、BC段坡面线存在明显的对称性，而CD段坡面线存在一块只有坡面短线而没有坡面长线的空白区且不与BC段对称，说明该区域的坡面长线因为找不到与其相交的坡面长线而被删除，即CASS算法没有完成所有坡面区域的填充。又如图3（b），其上棱线BC段与CD段夹角值较小，且BC段长度较小，生成的坡面线出现大量交叉情况。故上棱线段间的夹角、坡面线的间隔和长度是坡面线产生交叉的三个影响因素。

图3 南方CASS6.1软件生成的法线自然斜坡Fig.3 Normal－based natural slope created by South CASS6.1software

而CASS算法的贡献在于为斜坡图式提供一种绘制思路：如果找到最外围的一个交点（即初始实交点），并以该点对线段进行裁剪操作，则该线段就不会再与更小范围中的其他法线段产生交点。即只处理“相交”的坡面线，忽略上棱线角度和坡面线间隔的判断。然而，“初始实交点存在第一对相交法线段上”并不是一个好的科学表述，要在众多法线段中得到“第一对”相交法线段，需要进行大量空间运算和验证，导致自动化算法复杂，可操作性降低。而笔者发现初始实交点的位置呈现一定的规律性，只存在于相邻的两条法线上。所以，因循CASS算法的思路，基于“相邻”这一空间位置概念提出一种实交点存在性的科学表述——实交点定理。

2.3.2 实交点定理

实交点定理：初始实交点只存在于相邻的两条法线段上，而事实实交点则存在于初始实交点两侧的对称法线段上。

由定理可知，所有实交点必然是未经过裁剪操作的相邻法线段的交点。该定理优于CASS算法之处在于：① “相邻”这一空间位置概念的表述比“第一对相交法线段”更容易判断也更具一般性；② 实交点定理的初始实交点位置在上棱线的节点附近，而CASS算法的初始实交点位置则在坡面线附近，所以，根据实交点定理绘制的法线斜坡不会出现如图3（a）的空白区域；③表述简洁并足以描述一般形状的无交叉斜坡图式实交点的位置特征；④ 以该定理为核心的算法易于理解，操作简单，在一个由法线段组成的有序序列中（如从左到右），容易得到未经裁剪操作的相邻法线段。然而，基于实交点定理的算法与CASS算法都存在一个共同的缺陷就是不能处理特殊情况下（图3（b））的法线交叉问题。这是因为该算法只是解决在法线多边形内部不会出现交叉的问题，无法处理法线多边形外部的法线段与该多边形相交的特殊情况。所以，本文进一步提出实交点补充定理。

2.4 基于实交点定理及补充定理的算法描述

补充定理：若某连接上棱线与坡脚线的法线段与已经找到实交点的法线段相交于一点，则该交点是该法线段的事实实交点。

根据实交点定理及补充定理提出一种遍历及裁剪处理所有法线段生成无交叉法线坡面线的算法，称为基于实交点定理及其补充定理算法（ABRICT）。算法流程如图4所示。

3 理论证明

由2.3.1节可知，法线坡面线相交情况的产生源于三个要素，故可从三者的关系来论证某一绘制算法的通用性。而本节将从另一思路出发，采用反证法简单证明实交点定理只是寻找实交点生成无交叉法线坡面线的必要非充分条件，从而解释了基于实交点定理的算法或者与之类似的算法（如CASS算法）不适用于绘制所有形状的法线斜坡坡面线的原因。并进一步证明了ABRICT算法的充分性（通用性）。

图4 算法流程图（二维框图对应实交点定理部分，三维框图对应补充定理的增加部分）Fig.4 Flow chart of the algorithm（2Dframes illustrating the real－intersection theorem and 3Dframes illustrating the complementary theorem）

3.1 基于实交点定理算法生成无交叉坡面线的必要性证明

假设不使用基于实交点定理的算法也可以找到实交点并生成无交叉坡面线。即非对称法线段的交点也可能是实交点。

那么，若坡面线出现交叉的情况，则必然存在一个由上棱线和两条非对称的经过交叉部分裁剪处理的法线段组成的法线多边形，该多边形中至少含有一条不与其他法线段相交的法线段，从上棱线出发到达坡脚线，或者在到达坡脚线之前与该多边形外部的法线段相交（如图5的三种情况）。

图5 法线段（虚线）与法线多边形（点划线）关系示意图Fig.5 Illustrations of relationship between normalbased lines（dashed）and polygons（dash dotted）

已知法线多边形是封闭多边形，并且坡脚线在法线多边形外。再由2.1节前提假设②可知该坡面线不通过上棱线的节点。易知，经过封闭多边形边上任意一个异于顶点的点以及多边形外一点的直线，与该多边形的边至少有两个交点（该定理可以使用直线这一点集的紧致性和区域的连通性加以证明）。又由前提假设③知坡面线均与坡脚线同侧。故上述法线段必然与上述多边形相交。若该法线段相交于法线多边形的实交点，则与“非对称的法线段相交于实交点”的假设矛盾；若该法线段不相交于法线多边形的实交点，则与坡面线或者上棱线相交，此时的坡面线不再是无交叉坡面线，与“生成无交叉坡面线”的假设矛盾。故假设错误，必要性得证。即只有使用实交点定理的方法在相邻法线段上找到实交点，再对交叉部分进行裁剪处理才能得到无交叉坡面线。

3.2 基于实交点定理及其补充定理算法生成无交叉坡面线的充分性证明

假设使用实交点定理及其补充定理的算法不能得到无交叉坡面线。下面分“法线段与法线多边形关系”和“两法线多边形关系”两种情况讨论。

（1）任取一个法线多边形，它与到达坡脚线的法线段的关系分以下两种情况：① 法线段与法线多边形相交，由于经过实交点定理的方法处理后法线多边形内部不包含到达坡脚线的法线段，那么此法线段必从法线多边形的外部与多边形相交，这与补充定理矛盾，所以假设错误；② 法线段不与法线多边形相交，则生成的坡面线就是无交叉坡面线，假设错误。

（2）任取两个法线多边形，它们的空间关系分为以下三种情况：① 法线多边形重合，那么它与其他法线段的平面关系则转化成上述法线段与法线多边形关系的情况，它与其他法线多边形的平面关系则转化成分离或相交两种情况；② 两法线多边形分离，则生成的坡面线就是无交叉坡面线，假设错误；③ 两法线多边形相交，又分为两种情况。第一种情况，交点是法线多边形的一个顶点，若不再有其他交点，则两多边形不交叉，生成的坡面线是无交叉坡面线，故假设错误；第二种情况，交点是法线多边形一条边上异于顶点的一点，则沿多边形一边任取距离该交点左右两侧Δr的两点，当Δr→0时则必有一点位于另一多边形外部，与补充定理矛盾，假设错误。

综上，所有的情况下均不会出现法线段交叉的情况。即使用实交点定理及其补充定理的算法寻找实交点，然后再进行裁剪交叉部分操作可以生成任何形状（符合前提假设）的无交叉坡面线，充分性得证。

4 结果验证与分析

为了进一步验证算法的有效性，设计3组试验。试验结果表明，ABRICT算法在动态绘制任何形状（符合前提假设）的法线斜坡方面以及绘制的响应时间方面有良好的性能。所有试验的测试环境为1台CPU为Pentium 2.4GHz，512MB内存，80G硬盘的PC机。为提高准确度，第二、三组试验都运行30次，取其均值作为试验结果。需要说明，响应时间指自动生成坡面填充线的时间，不包括绘制上棱线与坡脚线的时间。

4.1 算法通用性对比验证

第一组试验选取浙江省建德市所辖16个乡镇中的5个作为试验对象，使用其地形图中的与斜坡图式类似的地貌数据，称为“类斜坡图式”。本组试验将采用ABRICT算法和CASS算法重新绘制这些地貌数据的坡面填充线。表1给出了“类斜坡图式”的数量。

表1 试验数据数量Tab.1 Data for the experiment

使用ABRICT算法的试验中共生成1 280 757条填充线，耗时6h19min 10s（说明实现计算机自动制图的必要性），得到的新地形图（局部，新安江街道建德大桥附近）如图6所示。使用人工判读方式，未发现交叉和漏绘坡面线。若每2mm间隔绘制坡面填充线（包括长短线）［1］，理论上需要绘制1 281 366条，试验结果比理论值少是因为试验数据中存在长度过小的类斜坡图式，上棱线长度不是2mm的整数倍。同时采用计算机自动统计方法（即用空间分析方法求出每条坡面线的交点个数，交点个数等于0或1的记录为无交叉，交点个数大于1的记录为有交叉，该方法虽有缺陷但是可以接受）检测所有的坡面线，未发现有交叉的记录。结果表明，与CASS算法相比，ABRICT算法在实际应用中具有很好的通用性。特别是，经试验结果分析发现，反复提到现有绘图软件无法处理“特殊形状”的斜坡图式并不“特殊”，在试验选择区域内的山地附近，斜坡或陡崖普遍都呈“U型”。如图6（a）中的“U型”斜坡呈现上棱线节点密集的情况，ABRICT算法也能够很好处理，而CASS软件绘制的图式则出现大量交叉和漏绘的情况（图6（b））。此外，对于上棱线节点密集的情况可以采用制图综合中的线段化简算法对上棱线进行预处理来提高效率，这将是今后对ABRICT算法进行改进的研究重点之一。

图6 通用性试验结果图（局部）Fig.6 Result of the experiment examining the generality

4.2 算法结果唯一性验证

第二组试验采用自左向右和自右向左的顺序遍历法线段生成如图7所示的斜坡图式。从图中可以看出，使用ABRICT算法生成无交叉法线斜坡的最终图案还与遍历法线段的方向有关。也就是说ABRICT算法的充分性只是说明采用该算法能够生成任何形状（符合前提假设）的无交叉法线斜坡图式，并不能说明生成的法线坡面线填充图案唯一。但是，无论遍历法线段方向如何，只要是依顺序遍历，生成的均为无交叉的斜坡图式。

4.3 算法效率验证

第三组试验研究交叉的坡面线数量增加对ABRICT算法性能的影响。对第二组试验中的斜坡图式进行横向扩展（上棱线向两边延长，得到三个含有124条、200条、306条坡面长线的斜坡）和纵向扩展（上棱线与坡脚线之间的距离增加）以增加ABRICT算法处理交叉坡面线的数量和坡面长线的总量（坡面线数量增加等价于坡面线间隔变小）。该组试验得到的三个试验数据如图8所示。从图中可以看出，在坡面长线数量一定的情况下，随着需要处理的相交法线段数量的增加，使用ABRICT算法生成无交叉法线斜坡图式的时间也随之增加，但是斜率较低说明增加缓慢。且三条拟合趋势线均呈现“低斜率高截距”的特征，说明影响绘制斜坡图式效率的主要因素是坡面长线段的生成过程，使用ABRICT算法寻找实交点和裁剪操作则是一个次要因素。由趋势线斜率随坡面长线总数的增加呈现递增规律可知，坡面长线总数的增加会提高遍历法线段的查询代价（算法今后改进重点之一），即坡面长线总数越大，使用ABRICT算法寻找实交点和裁剪操作对整个斜坡图式绘制效率的影响越大。

图7 ABRICT算法从不同方向遍历法线段绘制的斜坡Fig.7 Slopes drawn by traversing the normal segments in different order based on ABRICT algorithm

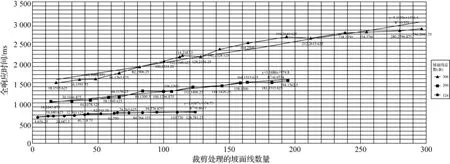
图8 坡面线数量增加对算法性能的影响Fig.8 Impacts of the number of slope lines on the efficiency of the algorithm

5 结 论

研究斜坡坡面线的图形生成方式，发现其图形由斜坡的上棱线和坡脚线决定，属于不规则地形图式符号的动态填充问题。并且，由法线法绘制的坡面线会出现交叉现象，影响图式的美观，若手动处理交叉线将是一个复杂的过程。ABRICT算法，不仅克服了原有技术的不足，而且揭示了“对称美”的普遍现象，对称地选取两条相邻的相交法线段，对其进行裁剪交叉线段的操作，生成的法线坡面线不再会产生交叉。此外，简单证明绘制这种简洁的无交叉坡面线的充要条件，并通过多组试验验证算法的有效性。也就是说，在四个前提假设之下，该算法在动态绘制地形图所需要的任何形状的法线自然（加固）斜坡、崩崖、陡崖、陡石山、堤岸等图式符号方面具有较好的适用性。同时，该算法也可为其他非规则的图案动态填充提供借鉴与启发。

［1］ CSBTS.GB／T 7929—1995.Specifications for Cartographic Symbols 1∶500，1∶1 000，1∶2 000Topographic Maps［S］.Beijing：Standards Press of China，1996：94－99.（国家技术监督局.GB／T 7929—1995.1∶500、1∶1 000、1∶2 000地形图图式［S］.北京：中国标准出版社，1996：94－99.）

［2］ PINEDA J.A Parallel Algorithm for Polygon Rasterization［J］.Computer Graphics（ACM），1988，22（4）：17－20.

［3］ MUKHERJEE M，CHAKRABORTY K.A Randomized Greedy Algorithm for the Pattern Fill Problem for DFM Applications［C］∥Proceedings of ISQED 2008.Palm Springs：IEEE，2008：344－347.

［4］ YANG Yong，LI Lin，WANG Hong，et al.Cartographic System Based on National Fundamental Geographic Data［J］.Geomatics and Information Science of Wuhan University，2008，33（3）：261－264.（杨勇，李霖，王红，等.基于国家基础地理信息数据的地图制图系统［J］.武汉大学学报：信息科学版，2008，33（3）：261－264.）

［5］ BAIN K A，GILES J R A.A Standard Model for Storage of Geological Map Data［J］.Computer and Geosciences，1997，23（6）：613－620.

［6］ HE Zhonghuan.Designing Technique of Complicated Linear Symbols in GIS Symbol Database［J］.Geomatics and Infor－mation Science of Wuhan University，2004，29（2）：132－134.（何忠焕.GIS符号库中复杂线状符号设计技术的研究［J］.武汉大学学报：信息科学版，2004，29（2）：132－134.）

［7］ CAI Xianhua，WU Li.Study of Symbol Library Data Structure and Algorithm Based on Property Unit［J］.Acta Geodaetica et Cartographica Sinica，2004，33（3）：269－273.（蔡先华，武利.基于特征元的符号库数据结构及算法探讨［J］.测绘学报，2004，33（3）：269－273.）

［8］ WANG Tonghe，YUE Chunsheng，ZHAO Fulai，et al.A Quick Drawing Algorithm for Map Symbols Based on Template in Embedded GIS［J］.Journal of Geomatics Science and Technology，2009，26（5）：330－332.（王同合，岳春生，赵夫来，等.基于模板的嵌入式GIS地图符号快速绘制算法［J］.测绘科学技术学报，2009，26（5）：330－332.）

［9］ ZHU Guorui，XU Zhiyong，WU Xiaofang.Design of Dynamic Map Symbol Based on Multi－transform Assembly［J］.Geomatics and Information Science of Wuhan University，2006，31（6）：548－551.（祝国瑞，徐智勇，吴小芳.基于多重变换组合的动态地图符号设计［J］.武汉大学学报：信息科学版，2006，31（6）：548－551.）

［10］ HURNI L，DAHINDEN T，HUTZLER E.Digital Cliff Drawing for Topographic Maps：Traditional Representations by Means of New Technologies［J］.Cartographica：The International Journal for Geographic Information and Geovisualization，2001，38（1）：55－65.

［11］ YANG Nai，GUO Qingsheng，SHEN Dayong.Automatic Modeling of 3DCliff Symbol［J］.Geomatics and Information Science of Wuhan University，2010，35（4）：411－414.（杨乃，郭庆胜，沈大勇.三维陡崖符号的自动建模研究［J］.武汉大学学报：信息科学版，2010，35（4）：411－414.）

［12］ LV Gan.Research on Database－driven Cartography and Its Processing System Framework［D］.Hangzhou：Zhejiang University，2008.（吕干.数据库驱动的制图建模及其数据处理框架研究［D］.杭州：浙江大学，2008.）

ANewAlgorithmforCreatingSlopeLineswithNoIntersections

FANGLei1，2，LIURenyi2，LVGan1，2，DUZhenhong1，2，YAOShenjun3
1.Zhejiang Provincial Key Laboratory of GIS，Zhejiang University，Hangzhou 310028，China；2.Department of Geographic Information Science，Zhejiang University，Hangzhou 310027，China；3.Department of Geography，The University of Hong Kong，Hong Kong 999077，China

This study develops a new algorithm to create any kinds of slope lines with no intersections automatically.It gives enough evidence to support that the real－intersection and the complementary theorem proposed in this research are sufficient conditions of the generation of slope lines without any intersections.This method can dynamically draw any kind of normal－based slopes，scarps，escarpments，steep rock hills or embankments.The efficiency of the algorithm is tested by using three experiments.

slope；filled hatch；cartography；geographic information system

FANG Lei（1982—），male，PhD candidate，majors in GIS applications and GIS algorithms.

1001－1595（2011）04－0524－07

P208

A

国家863计划（2007AA12Z182；2009AA12Z222）；中国国家博士后基金（20070421161）；浙江省重点攻关基金（2007C23091；2009C33011）；教育部博士点基金（20060335040；200803350017）

宋启凡）

2010－04－02

2010－10－28

方雷（1982—），男，博士生，主要从事GIS应用系统和算法方向的研究。

E－mail：rainfield.f＠gmail.com