GRACE时变重力位系数误差的改进去相关算法

詹金刚，王 勇，郝晓光

1.中国科学院测量与地球物理研究所，湖北武汉430077；2.中国科学院研究生院，北京100049

1 引 言

重力场及其变化反映了地球表层和内部的物质密度分布及运动状态。因此，根据重力场的时空变化，可以推演和监测地球系统物质运动和交换过程。过去，人们主要通过地面重复重力测量获得重力场随时间的变化信息。由于地面连续重力观测站点相对较少，高精度的重复重力观测又较耗时，难以获得连续的时空重力场信息。2002年GRACE的成功运行使得研究地球重力场随时间的变化信息成为现实。起初，由于GRACE资料解算得到的时变重力场的精度较差以及资料积累的周期较短，主要利用GRACE资料验证和研究大尺度上的重力季节变化［1－9］，国内也有一些学者利用GRACE资料对重力场的恢复方法、仿真及在海平面变化中的应用等方面进行研究并取得一定成果［10－12］。随着重力场恢复方法的改进和滤波技术的进一步提高，目前由一个月的GRACE重力卫星资料反演大地水准面的精度在400km尺度上已达到1～2cm［13－14］。

针对GRACE卫星资料，目前展开的工作主要包含两方面：一是利用GRACE资料解算时变重力场模型，二是时变重力场的应用。由于目前解算的GRACE时变重力场模型的高阶系数存在较大的误差，由模型系数恢复地球时变重力场结果中表现为严重的条带误差，给地球物理信号的识别带来一定的困难，因此必须进行滤波提高信噪比。针对消除条带误差常用的处理方法，按照其滤波思想主要分为两类：一类是通过引入滤波因子，降低模型高阶系数的权重，从而达到平滑的效果，这类方法主要包括各向同性和非各向同性的高斯滤波、维纳滤波以及扇形滤波［15－18］，其实质是以牺牲模型的空间分辨率为代价来换取空间平滑的效果，滤波半径越大，模型空间分辨率的牺牲程度也越大；另一类方法是通过消除模型系数之间的相关误差，从而达到去条带误差的效果，这类方法主要包括文献［19］的基于阶l的变滑动窗多项式拟合去相关误差方法，文献［20—21］提出的多项式拟合去相关误差方法以及文献［22］提出的基于阶l次m的变滑动窗多项式拟合去相关误差方法。其中尤以文献［19］提出的滑动窗多项式拟合去相关误差方法效果最为显著，文献［22］的滤波方法计算过于复杂，而滤波效果和文献［19］的滑动窗多项式拟合去相关误差方法并无显著差异。这类方法的优点是直接消除系数间的相关误差，而不会牺牲模型的空间分辨率，其缺点是在赤道附近区域去条带误差的效果并不显著。基于上述原因，通常采用将两类滤波技术相结合的组合滤波方法。

第二类去相关误差方法效果的优劣，直接决定着高斯滤波半径选取的大小。去相关误差效果越显著，则高斯平滑半径的选取就越小，对模型空间分辨率的损失也就越小；反之，则对模型空间分辨率的损失越大。文献［19］提出的变滑动窗多项式拟合去相关误差方法在赤道两侧区域取得了很好的去条带误差效果，但因其在文献中并没有公开具体的实现步骤，因而许多学者按照其思想滤波时并未实现其文献中的理想效果，目前国际上根据其思想常用的做法是采用多项式拟合去相关技术，而没有采用滑动窗［20－21］。根据文献［19］的思想，针对滑动窗的特点，详细分析了滑动窗在时变重力场数据处理中的不足，提出滑动窗多项式拟合去相关误差的改进方法。将改进方法应用于GRACE时变重力场数据处理时，在赤道两侧区域取得了较为显著的去条带滤波效果。

2 滑动窗多项式拟合去相关误差方法的改进

在抑制条带噪声方面，文献［19］提出的滑动窗多项式拟合去相关方法的思想是：固定时变重力场模型的次m，对模型系数的偶数阶系数序列（l＝0，2，4，…）以及奇数阶系数序列（l＝1，3，5，…）分别采用滑动窗多项式拟合，并以该拟合值作为相应系数的相关误差改正值。这里以窗口宽度为7点，m＝11和45时为例说明（假定模型最大展开为60阶）：当m＝11时，系数序列为C11，11、C13，11、C15，11、C17，11、C19，11、…、C51，11、C53，11、C55，11、C57，11、C59，11。由于窗口的宽度为7点，按照滑动窗的基本原理，得到去相关误差改正的系数依次是C17，11、C19，11、…、C51，11、C53，11，这样数据序列的两端各有三个系数没有得到去相关误差改正。当m＝45时，系数序列C45，45、C47，45、C49，45、C51，45、C53，45、C55，45、C57，45、C59，45中仅有C51，45、C53，45两个系数得到去相关误差改正，而数据序列两端的其他6个系数并没有得到去相关误差改正。这种情况下，滑动窗多项式拟合去相关误差改正方法实际上已经没有多大意义，因为没有得到误差改正或者说舍弃的系数数量已远大于改正系数的数量。显然滑动窗去条带误差方法在m＞45时，已经失去了去相关误差改正的作用和意义。

为减少两端数据的舍弃，同时使得滑动窗多项式拟合去相关误差方法在模型系数的更高次数m上得到应用，本文根据相邻高阶系数间具有相关误差这一特点，在数据处理时，先对数据序列的两端做反向边界延拓，向边界两端各延伸1／2窗宽的数据。仍然以窗口宽度为7点，m＝11为例说明（假定模型最大展开为60阶），经反向边界延拓后，系数序列变为－C19，11、－C15，11、－C13，11、C11，11、C13，11、C15，11、C17，11、C19，11、…、C51，11、C53，11、C55，11、C57，11、C59，11、－C57，11、－C55，11、－C53，11。这样，在计算C13，11系数的误差改正时，用到了－C15，11、－C13，11、C11，11、C13，11、C15，11、C17，11、C19，117个系数间的相关性。这样处理后，不但使得原数据序列两端的数据得到滑动窗多项式拟合去相关误差改正，同时也使得滑动窗去相关误差方法可以在更高阶次系数中得到应用。图1是滑动窗多项式拟合去相关误差方法改进前后的系数变化曲线。图1（a）与图1（b）为普通滑动窗结果，（a）为每阶系数变化曲线，（b）为奇偶阶系数变化曲线；图1（c）与图1（d）为改进后的滑动窗结果，（c）为每阶系数变化曲线，（d）为奇偶阶系数变化曲线。从图1中可以明显看出，模型系数经原滑动窗多项式拟合去相关误差方法改正后，高阶次的系数仍然存在较大的误差，表现为高阶次的系数变化不收敛，例如m＝15、18时尤为明显；图1（c）、（d）显示，模型系数经改进后的滑动窗多项式拟合去相关误差方法处理后，模型系数随着阶l的增大趋于稳定和收敛，表明系数受误差的影响较小。例如当m＝15时，经改进后的滑动窗多项式拟合去相关误差方法处理后，高阶次系数误差得到显著改善，曲线变化的幅度减小了一个量级。

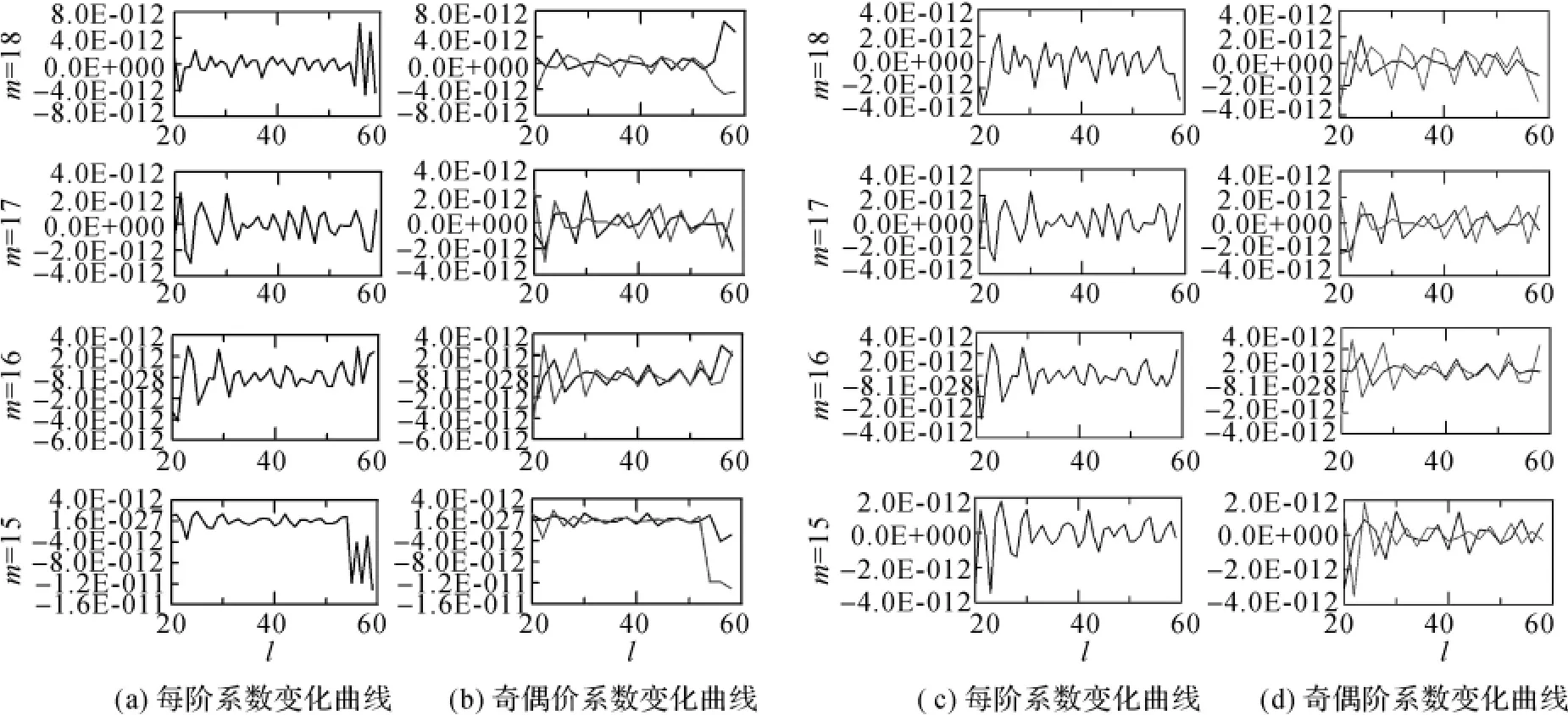
图1 去相关误差方法改进前后系数变化曲线对比Fig.1 Coefficients change before and after improvement of de－correlation method

3 效果对比与检验

为检验改进后数据处理方法的效果，以CSR RL04数据为例进行验证。由于在RL04数据的解算中，引入了更高精度的地球重力场背景模型、海潮模型以及极潮模型等，使得模型的低阶次系数的精度得到进一步提高，系数变化曲线显示系数间相关误差在m≥15时开始越来越明显；其次，CSR RL04数据的阶能谱显示模型系数约在l≥15时，系数误差逐渐震荡放大。综合以上因素，本文选取在m≥15时，开始做去相关误差改正，而对于低阶系数尽量不做改动。文献［19］和文献［22］中，对低阶次系数去相关误差改正采用了较大的窗口宽度。这主要是因为模型低阶次系数间的相关误差小或者说其精度相对较高，利用大的窗宽进行弱相关的多项式拟合，以减小对低阶次系数的改正量。由于本文采用精度较高的RL04数据且起算阶数取为15，所以采用固定的窗口宽度。大量数据试算后发现，窗口宽度越大，去条带误差效果越差，表现为结果中的条带噪声越明显，而当窗口宽度为5时，计算结果过于平滑，有效信号的幅度削弱过多。因此，本文计算中选择窗口宽度为7点，多项式拟合次数为3。

图2为随机抽取的2008年1～4月GRACE时变重力场模型计算结果。其中，图2（a）为没有进行任何滤波的月重力异常结果，从图中可以看出月重力异常结果主要表现为条带噪声。图2（b）、（c）分别为滑动窗去相关误差方法改进前后的重力异常图。从图2（b）、（c）中可以明显看出，改进后的方法在赤道两侧区域抑制条带噪声的效果得到显著改善，说明了新方法在赤道两侧区域抑制条带误差的有效性。此外，对2003年1月至2008年12月共72个月的GRACE数据进行了验证对比和统计。统计结果表明：新方法在赤道两侧区域抑制条带噪声的效果较原方法均具有显著的改善。这一结果有效证明新方法在GRACE数据处理中抑制条带误差的有效性。

图2结果说明了滑动窗去相关误差的改进方法在抑制条带误差方面的效果及有效性。在证明新方法去条带误差的有效性之后，通常还需要验证该方法的正确性，即新方法是否会对真实信号产生扭曲以及是否会产生虚假信号。为此，采用全球陆地资料同化系统GLDAS土壤湿度模型数据作为验证。GLDAS模型同化了四个不同的全球水文模型，并采用NASA新一代的空间对地观测技术和地面数据来约束地球表面的状态，进而获得地球表面的近实时信息，是目前最好的全球水文模型之一［23］。土壤湿度变化对全球重力场变化趋势的影响如图3所示，其中图3（a）为没有采用任何滤波器的结果，图3（b）为只采用滑动窗去相关误差改进方法的滤波结果。从图3中可以看出，滑动窗去相关误差改进方法除在高纬度地区对信号的强度或振幅稍微有削弱外，并没有改变信号的位置和形状，也没有产生虚假信号。图3结果证明本文提出的滑动窗去相关误差改进方法的可靠性和正确性。

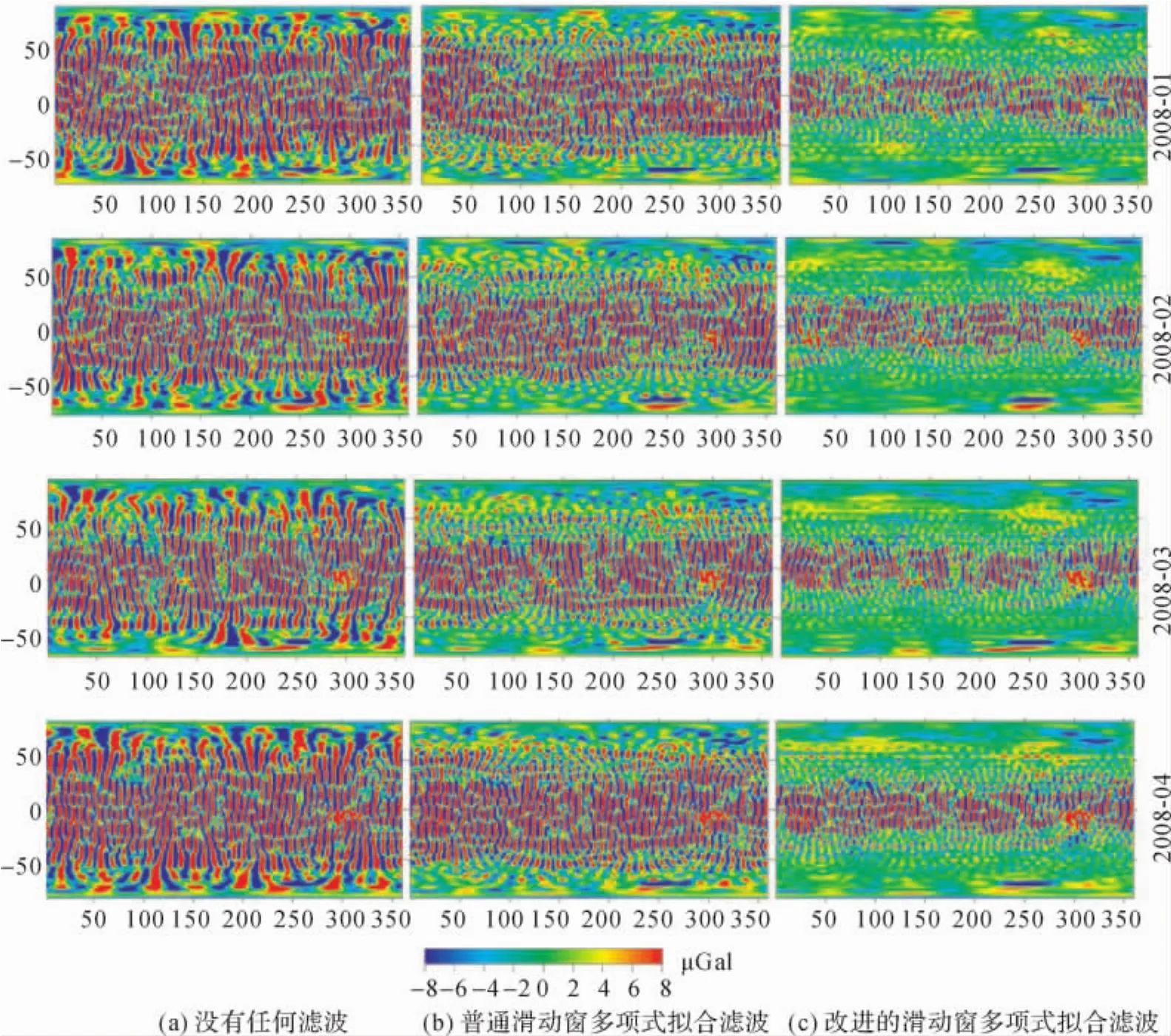
图2 GRACE月重力异常图Fig.2 Maps of monthly anomaly of GRACE gravity field（1Gal＝1cm／s2）

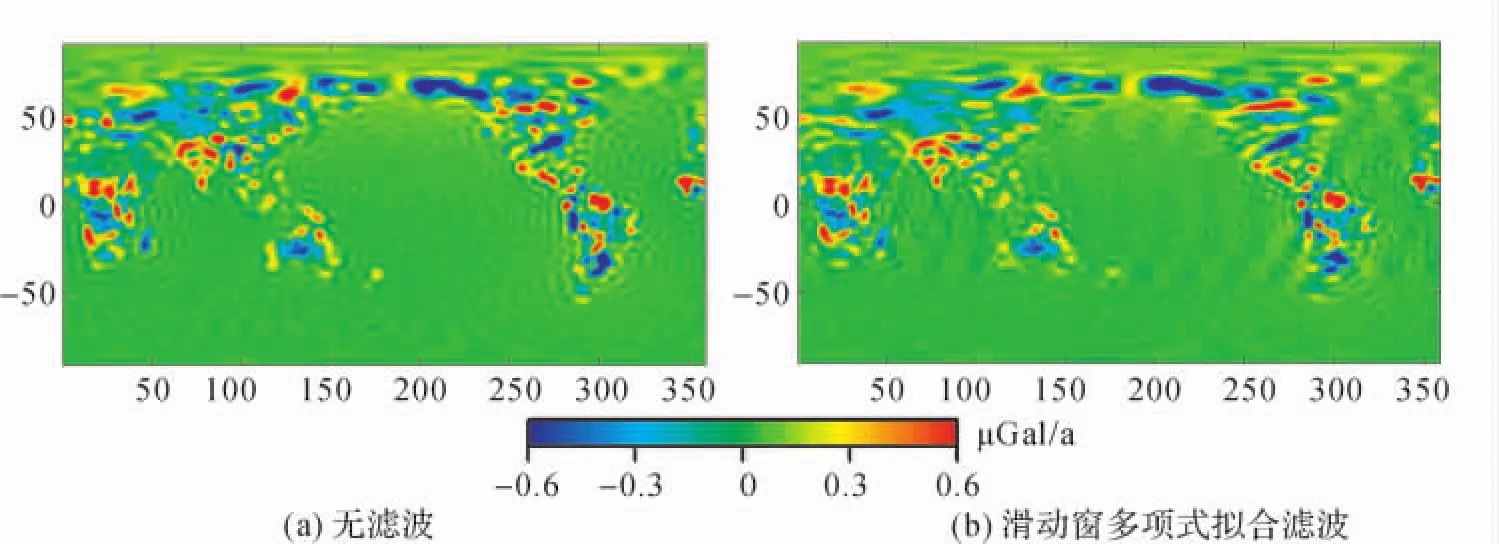
图3 去相关误差改进方法对重力场变化趋势的影响Fig.3 Effects of improved de－correlation method on gravity trend

4 结 论

（1）在滑动窗多项式拟合数据处理技术上做了相应改进，改进后的数据处理方法在不影响原滑动窗去相关误差方法的前提下，不仅使得数据序列两端的系数得到去相关误差改正，而且使得滑动窗去条带误差技术能够应用到模型的更高阶次。将改进后的滑动窗多项式拟合去条带误差方法应用于CSR解算的GRACE数据时，在抑制条带噪声的效果和误差的改善范围上较改进前方法结果均有显著提高，表明新方法对于消除模型系数间的相关误差具有显著效果。

（2）将改进方法应用于全球土壤湿度变化数据，计算土壤湿度变化对全球重力场变化趋势的影响。计算结果表明，本文提出的改进方法仅对高纬度区域内信号的强度即振幅变化有稍微消弱，而对信号的位置和形状并没有明显的改变，也没有产生虚假信号。

［1］ TAPLEY B D，BETTADPUR S，RIES J C，et al.GRACE Measurements of Mass Variability in the Earth System［J］.Science，2004，305（5683）：503－505.

［2］ VELICOGNA I，WAHR J.Measurements of Time－variable Gravity Show Mass Loss in Antarctica［J］.Science，2006，311（5768）：1745－1756.

［3］ HU Xiaogong，CHEN Jianli，ZHOU Yonghong，et al.Seasonal Water Storage Change of the Yangtze River Basin Detected by GRACE［J］.Science in China：Series D Earth Sciences，2006，49（5）：483－491.（胡小工，陈剑利，周永宏，等.利用GRACE空间重力测量监测长江流域水储量的季节性变化［J］.中国科学：D辑地球科学，2006，36（3）：225－232.）

［4］ ZHONG Min，DUAN Jianbin，XU Houze，et al.Trend of China Land Water Storage Redistribution at Medi－and Large－spatial Scales in Recent Five Years by Satellite Gravity Observations［J］.Chinese Science Bulletin，2009，54（5）：816－821.（钟敏，段建宾，许厚泽，等.利用卫星重力观测研究近5年中国陆地水量中长空间尺度的变化趋势［J］.科学通报，2009，54（9）：1290－1294.）

［5］ WANG Hansheng，WANG Zhiyong，YUAN Xudong，et al.Water Storage Changes in Three Gorges Water Systems Area Inferred from GRACE Time－variable Gravity Data［J］.Chinese Journal of Geophysics，2007，50（3）：730－736.（汪汉胜，王志勇，袁旭东，等.基于GRACE时变重力场的三峡水库补给水系水储量变化［J］.地球物理学报，2007，50（3）：730－736.）

［6］ E Dongchen，Yang Yuangde，Chao Dingbo.The Sea Level Change from the Antarctic Ice Sheet Based on GRACE［J］.Chinese Journal of Geophysics，2009，52（9）：2222－2228.（鄂栋臣，杨元德，晁定波.基于GRACE资料研究南极冰盖消减对海平面的影响［J］.地球物理学报，2009，52（9）：2222－2228.）

［7］ XIAO Yun，XIA Zheren，WANG Xingtao.Recovering the Earth Gravity from Inter－satellite Range－rate of GRACE［J］.Acta Geodaetica et Cartographica Sinica，2007，36（1）：19－25.（肖云，夏哲仁，王兴涛.用GRACE星间速度恢复地球重力场［J］.测绘学报，2007，36（1）：19－25.）

［8］ ZHOU Xuhua，WU Bin，XU Houze，et al.Resolution Estimation of Earth Gravity Field Recovery through the Low－low Satellite to Satellite Technology by Numerical Simulation［J］.Chinese Journal of Geophysics，2005，48（2）：282－287.（周旭华，吴斌，许厚泽，等.数值模拟估算低低卫－卫跟踪观测技术反演地球重力场的空间分辨率［J］.地球物理学报，2005，48（2）：282－287.）

［9］ ZHOU Xuhua，XU Houze，WU Bin，et al.Earth’s Gravity Field Derived from GRACE Satellite Tracking Data［J］.Chinese Journal of Geophysics，2006，49（3）：718－723.（周旭华，许厚泽，吴斌，等.用GRACE卫星跟踪数据反演地球重力场［J］.地球物理学报，2006，49（3）：718－723.）

［10］ ZOU Xiancai，LI Jiancheng，JIANG Weiping，et al.Research on the Simultaneous Solution Method for Satellite Gravity Data Analysis and Its Simulation［J］.Acta Geodaetica et Cartographica Sinica，2010，39（4）：344－348.（邹贤才，李建成，姜卫平，等.卫星重力资料分析的同解法研究及其仿真［J］.测绘学报，2010，39（4）：344－348.）

［11］ JIANG Tao，LI Jiancheng，WANG Zhengtao，et al.Global Sea Level Variations from Combined Jason－1and GRACE Data［J］.Acta Geodaetica et Cartographica Sinica，2010，39（2）：135－140.（蒋涛，李建成，王正涛，等.联合Jason－1与GRACE卫星数据研究全球海平面变化［J］.测绘学报，2010，39（2）：135－140.）

［12］ XIAO Yun，XIA Zheren，WANG Xingtao.Recovering the Earth Gravity Field from Inter－satellite Range－rate of GRACE［J］.Acta Geodaetica et Cartographica Sinica，2007，36（1）：19－25.（肖云，夏哲仁，王兴涛.用GRACE星间速度恢复地球重力场［J］.测绘学报，2007，36（1）：19－25.）

［13］ BETTADPUR S.Level－2Gravity Field Product User Handbook［EB／OL］.Austin，Texas：University of Texas.2003－12－01［2010－03－10］.http：∥www.csr.utexas.edu／grace／publications／handbook／L2－User－Handbook＿v1.0.pdf.

［14］ TAPLEY B D，BETTADPUR S，WATKINS M M，et al.The Gravity Recovery and Climate Experiment：Mission Overview and Early Results［J／OL］.Geophy Research Letters，2004，31：1－4［2010－03－10］.http：∥www.spaceweather.ac.cn／publication／jgrs／2004／Geophysical% 20Research%20Letters／may／2004GL019920.pdf.

［15］ WAHR J，MOLENAAR M，BRYAN F.Time Variability of the Earth’s Gravity Field：Hydrological and Oceanic Effects and Their Possible Detection Using GRACE［J］.Journal of Geophysical Research，1998，103（B12）：30205－30229.

［16］ HAN S C，SHUM C K，JEKELI C，et al.（2005），Nonisotropic Filtering of GRACE Temporal Gravity for Geophysical—Signal Enhancement［J］.Geophysical Journal International，2005，163（9）：18－25.

［17］ SASGEN I，MARTINEC Z，FLEMING K.Wiener Optimal Filtering of GRACE Data［J］.Studia Geophysica et Geodaetica，2006，50（4）：499－508.

［18］ ZHANG Z H，CHAO B F，LU Y，et al.An Effective Filtering for GRACE Time－variable Gravity：Fan Filter［J］.Geophysical Research Letters，2009，36：1－6.

［19］ SWENSON S，WAHR J.Post－processing Removal of Correlated Errors in GRACE Data［J］.Geophysical Research Letters，2006，33：1－6.

［20］ CHAMBERS D P.Evaluation of New GRACE Timevariable Gravity Data over the Ocean［J］.Geophysical Research Letters，2006，33：12－16.

［21］ CHEN J L，WILSON C R，TAPLEY B D，et al.GRACE Detects Coseismic and Postseismic Deformation from the Sumatra－Andaman Earthquake［J］.Geophysical Research Letters，2007，34：33－37.

［22］ DUAN X J，GUO J Y，SHUM C K.et al.On the Post－processing Removal of Correlated Errors in GRACE Temporal Gravity Field Solutions［J］.Journal of Geodesy，2009，83（11）：1095－1106.

［23］ RODELL M，HOUSER P R，JAMBOR U.et al.The Global Land Data Assimilation System［J］.Bulletin of American Meteorological Society，2004，85：381－394.