讲授观的嬗变:从注入到“过程→生成”——基于高等数学教学探讨

王积社

（韩山师范学院数学与信息技术系，广东潮州 541021）

讲授观的嬗变:从注入到“过程→生成”
——基于高等数学教学探讨

王积社

（韩山师范学院数学与信息技术系，广东潮州 541021）

培养科学技术发明创造人才，数学教育至关重要.然而尽管新教法的研究如火如荼，但在实际教学中却很难实施，尤其是高数教学，仍然继续着传统的“定义→性质→定理→例题”的注入方法，如此下去非常危险，所以改革传统的数学讲授观念是急中之急.展望科学发展的诉求，基于过程哲学、意会哲学理论解读新课改的三维目标，提出了“过程→生成”讲授观，并论述了实施要点.

过程哲学；意会哲学；讲授观；“过程→生成”讲授法

高等数学教学中如何提高学生的数学素养，如何培养科学技术发明创造型人才，我们必须以实相待.笔者认为首要问题是讲授观的变革，本文浅谈笔者的观点.

1 如此讲授如何得了

素质教育已经多年，然而翻开高数教材，查阅精品课件，走进高数课堂，几乎仍是“定义→性质→定理→例题”的注入模式，这种模式作为数学结果的表述堪为精湛，但是作为数学的教学模式却无益于数学素质的提高，无益于科学技术发明创造人才的培养.因为直接给出定义、性质、定理，学生就只能看到庞大而复杂的数学机器，却得不到发明这台机器的真谛，就只能书云我云，只会做从已知到求证的游戏，不会做从已知到未知的探索，更不想从未知到未知的创造，丧失了数学精神和创造能力；因为把相关的知识搞得支离破碎，使学生只见树木不见森林，丧失了整体思维能力；因为重理论而不重应用，数学变得乏味难懂，使学生产生了惧学、厌学、逃学等不良行为．如此下去如何得了？

2 新型教法为何萧条

笔者在中国知网以题名检索，从2000年1月1日到2011年6月10日，关于研究性学习、自主学习、合作学习、探究学习的研究论文分别有10 701、16 067、10 208、5 178篇，而讲授法的仅有203篇；时过20天，相应结果变为10 766、16 314、10 382、5 271、207篇.又全国教育科学十五规划项目中有关研究性学习的24项，而无讲授法.可见新教法研究如火如荼，讲授法研究却门庭冷落．但实际课堂却截然相反，尤其是高校，传统的讲授法独霸讲堂，新型的教学法却难见踪影.为何如此？情况是复杂的.单析教学因素：客观上受教学条件的限制，如新教法需要更多的教学时间，然实际课时却远远不够，除非不顾知识的系统学习，但这是不希望的，因为今日美国的数学教育也在着重强调数学基础[1]，而讲授法却具有准确、高效、快捷、系统等优势，能在规定时间内系统完成教学任务；又如我国高校班容量过大[2]（笔者所在学校如数学分析、高等代数等专业基础课也常是100多人的合班上课），新教法根本无法操作，但讲授法却能应对自如，等等．主观上受传统教学观的禁锢，如“定义→性质→定理→例题”似乎为数学教学的法定模式，笔者很不理解，为何形如“情景；定义→性质→定理；解答情景问题”的讲授方法能在教学大赛中屡屡获胜？为什么面对一个很好的“情景”，就不能顺着解决情景问题的思路推出所有，却一定要转到“定义→性质→定理”的注入模式？这是观念问题，如果传统的讲授观不被弃绝，那么任何新教法都将沦落为传统模式的“变种”，改革也即被架空．

3 讲授法的审度

已经看到：教学离不开讲授法，但容不得传统的讲授法，而重在讲授观.那么如何理解讲授观？讲授法是否等同于注入式、满堂灌？需要厘清.首先讲授法是“教师通过口头语言向学生描绘情景、叙述事实、解释概念、论证原理和阐明规律的教学方法”[3]142，而注入式是“教师在教学中，不顾学生学习认识过程的客观规律及他们的理解能力和知识水平,把现成的知识结论灌输给学生，主观地决定教学过程，并强迫学生呆读死记的教学方法”[3]568，满堂灌是“缺乏启发性而又全堂课一讲到底”的教学方法[4]76．可见讲授法既不等同于注入式，也不等同于满堂灌．实际上讲授是教学的基本的行为，任何教法都无法弃之，但是不同的讲授观会形成不同的讲授法，如“注入式（满堂灌）＋讲授法＝注入式（满堂灌）的讲授法”，我国传统的讲授法即是受苏联凯洛夫教育理论影响而形成的注入式的讲授法．因此我们不应该拒斥讲授法，而应该拒斥注入式的讲授法，且创建适时宜的讲授法，比如“互动式讲授法”、“探究式讲授法”、“活动式讲授法”未尝不可.总之我们需要寻求一种适合素质教育及培养科学技术发明创造人才的讲授观来作为教学的基本理念．

4 讲授观的断诀

培养科学技术发明创造型人才，要适应科学发展的需求．钱学森指出“21世纪，不管哪一门学科，都离不开对系统的研究”[5]．关于系统，其的特征是整体，本质是关系，方法是还原论与整体论的辩证统一，亦即是在分解研究的基础上综合集成到整体而实现1+1＞2的涌现，最终从整体上研究和解决问题.文献[6]指出“有必要将系统作为过程来认真对待：系统思维要求用过程分析来揭示系统的过程结构；系统思维重在把握过程系统的整体涌现性；人的过程思维能力，必须有意识地培育”．所以提高学生素质，培养科学技术发明创造型人才，就必须培育学生的过程思维能力，使学生具有良好的系统科学思想．

论及过程，首先应选择怀特海的过程哲学为基本的思想观念．过程哲学认为：事物都处于永不停息、转瞬即逝的生成和发展过程中（过程思维）；自然、社会和思维乃至整个宇宙都是有生命的机体（整体思维）；万物皆某种方式相互关联，这种关联只能通过摄入方式实现（关系思维）；过程是多种实际存在物合生出单一实际存在物的活动过程（涌现思想）；对实际存在物的分析即是对摄入的分析，而实际存在物的生成则是系列摄入阶段的合生（还原论与整体论的辩证统一）.可见过程哲学具有系统思维特征，有益于指导科学技术发明创造型人才的培养.怀特海指出“实际存在物的生成方式构成了这个实际存在物是什么”[7]，因此理解事物就必须理解其生成过程，学习知识就必须学习其生成过程，良好的讲授就应该充分体现知识、技能的生成过程.

其次应选择波兰尼的意会哲学作为基本的认知方法.波兰尼指出：人类的知识由意会知识（不可言传的知识）和言传知识（能够以书面文字、图表和数学公式加以表述的知识）两部分构成[8]110，科学发现不能通过明确的论述来获得，只能由思想的意会能力来达到[9]．可见意会知识对培养科学技术发明创造人才的重要意义，因此数学教学中如何解决定义、定理的“不可言传”性就非常关键.注意到波兰尼的“不可言传”只是“否认我能恰当地谈论它”[10]，于是关键的把握就在于如何“恰当地谈论它”．波兰尼认为[8]117，无论词语、符号都无法通过它们自身来理解它们所示信息，信息的传递效果最终取决于信息接收者对信息的知性理解，而理解的功能在于“探求我们的意图是什么、我们的意思是什么、我们正在做什么”，即强调意会认知是“摄悟的过程”[8]121．因此教学应该设计具有理解功能的摄悟过程，设计“类似于人类完成新发现的创造性的重组过程[8]118”．

在此把意会认知与过程哲学并论，是因为它们具有非常相似的观点．譬如过程哲学认为事物的本质是生成过程，摄入是生成的核心；意会认知认为识知的本质是意会过程，摄悟是意会的基石．再如过程哲学与意会认知都具有整体、生成、创造、开放等共性[11,12]，且这些性质都切合于系统科学思想．

最后落脚到基础教育新课改的三维目标，因为三维目标中提出了“过程与方法”．基于过程哲学及意会认知理论解读三维目标，其中的“过程”即是强调知识、技能的生成过程、突显知识、技能的意会过程；“方法”即是知识、技能的生成方法（过程与方法的关系可类似于计算机理论中的进程与程序的关系理解），于是三维目标的基本理念是“过程化地识双基”．谈到双基，有论者指出“美国是在创新有余而基础不足的基础上强调加强基础教育，而我国正与其相反，是基础有余而创新不足，因此，必须要加强创新教育，弥补自身的不足”，但笔者认为，我们远未达到“基础有余而创新不足”，而应是“基础无力且创新不足”，因为我们的基础是强行注入的，存在着根系浅弱、活力不足的严重缺陷，在此基础上播下创新种子，也很难获得丰硕成果．所以改革的任务并非是“在已有的基础上加强创新教育”，而应是彻底改变僵化的教育现状，在构建活力基础的进程中加强创新教育．然而“过程化地识双基”的理念给出了实现任务的有效途径，因为只有充分理解知识、技能的生成过程，才能使双基在学生心中深深地扎根，只有长期体验知识、技能的生成过程，才能潜移默化地使学生形成创造性的意会知识．所以三维目标不仅是对基础教育改革的要求，也应是高等教育改革的基本要求．

至此已经明确：应该以“过程化地识双基”为基本理念，以过程哲学、意会认知论为思想方法，构建“体现知识、技能生成过程”的讲授观（简称为“过程→生成”讲授观）．关于三维目标，笔者不赞同“像立方体的长、宽、高”的比喻，因为立方体的长、宽、高是分立的，是有度量的，然而“物质活动和精神活动难解难分地相互交织在一起”[13]，我们绝无可能分而立之，更无可能分而测之（实际上“知识与技能、过程与方法、情感态度与价值观”是《基础教育课程改革纲要》对课程标准的基本要求，而“三维目标”只是人们的简称，不过如此简称的确有失本意），根据过程哲学的流变原理，笔者认为喻之为“三维过程流”更能体现其动态、交融、变化、生成等特征，于是基于三维目标的教学应该“始于某种背景，受到思想、情操的层层支配，激起对学习目标的步步追求，诱导已有知识、技能、方法的循循摄入，形成流变与合生：在流变中创造新知识、练就新技能、获得新方法、增长新智慧、提升价值观、提高创造力”，这也是对“过程→生成”讲授观的诠释．

5 “过程→生成”教学的基本原则

因为知识、技能的生成过程本无定式，所以“过程→生成”教学如何设计取决于教师对具体问题的诠释力，不过要遵循一些基本原则.

1 整体性.

系统科学的特征是整体，怀特海认为“教育需要解决的问题就是使学生通过树木看见森林”[14]12，波兰尼认为意会认知过程要“将互相脱节的细部整合成一个综合的整体”[8]121，所以“过程→生成”教学必须注重内容、思维的整体性，注重探究过程的整体涌现性．如传统的近世代数教材或教学中都把模的剩余类、剩余类加群、剩余类环分割在不同的章节中讲解，破坏了知识、思维的整体性.笔者讲近世代数时是三者一气呵成的：（1）分析计时方法构建剩余类Z24；（2）研究时间计算问题定义Z24上的加法，进而生成剩余类加群(Z24,+ )；（3）类比加法定义乘法，比较(Z24,+ )生成剩余类乘半群(Z24,·)；（4）综合(Z24,+)与(Z24,·)生成剩余类环(Z24,+,·)；（5）简析其它类似例子；（6）形式上推广到Zm、(Zm,+)、(Zm,·)、(Zm,+,·)；（7）理论探讨：严格定义分类；研究分定义的合理性；研究性质；（8）构建模的剩余类、剩余类加群、剩余类环的概念体系.

2 活力性.

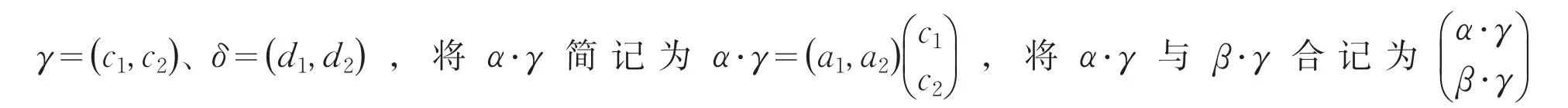
3 动态性.

动态是过程哲学与意会哲学的基本原则，所以“过程→生成”教学要体现动态性．如何动态，也无定式，不过基本地说，教学设计上可参照怀特海的“教育节奏”[14]27论，或参照怀特海的“反应、补充、满足”三阶段感受过程论[15]386，或参照波兰尼意会认知的from-to结构论[16]，或参照波兰尼的“学习行为”论[10]104等等，当然更应参考我们已有的教育研究优秀成果，限于篇幅不多累赘；具体教学中要注重师生、生生间的互动（言行、情感、思维的交流活动），学生与教师思维的同步活动，及形成知识及其关系、方法、相关信息所成的能动系统（如图1所示的多项式整除性的知识系统）．

4 摄入性.

摄入是过程哲学用来揭示实际存在物之间的相互关系的思维方法，是“对具体要素的每一占有过程[15]402”，摄入理论对教学有重要的指导意义．首先怀特海把教学中的摄入比喻为“有机体吸收食物”[14]59．因此好的讲授犹如营养美餐，既能满足学生的需求，又能使学生乐于接受，这就需要精心的教学设计与高超的教学艺术.其次怀特海认为主体与客体都是认识过程中的突现物[13]，每个摄入阶段中，执行摄入功能者是主体，被摄入的对象是客体，主、客关系随着摄入过程的结束而告终．怀特海的主、客突现论解决了教学中主客对立矛盾：教学过程由一系列“摄入过程”构成，不同的摄入过程有不同的主体．例如当教师酌情诱导时教师就成为主体，当激起学生感受时学生就成为主体，当某种现象摄入相关资源形成定理时，该现象即为主体，等等．这样即可有效地避免“注入式”、“满堂灌”及“一言堂”．

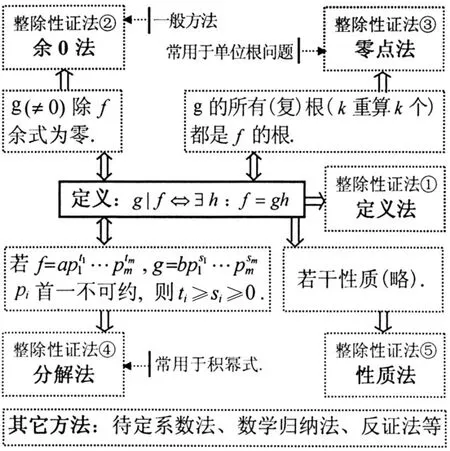
图1 多项式整除性的知识系统

5 连续性.

怀特海认为“在合生过程中，存在着一种连续状态，其中，新的摄入通过整合以前的摄入而产生”[15]44．因此生成是已有摄入连续产生新的摄入的合生过程，它是非线性的，知识、技能的生成也是这样.如基于24时计时法，通过各种客观事实及理性分析的摄入生成了Z24；……当生成了(Z24,+)与(Z24,·)后，随即合生出(Z24,+,·)……，这一切都是连续的．又如“情景；定义→性质→定理；解答情景问题”的方法是不连续的．再如文献[17]给出的案例教学模式，既缺少连续性又缺少生成性：其一，在“如何选择合适的砂轮？这就需要用到‘曲率、曲率圆及曲率半径’的新知识”中缺少了“选择”与“需要”间的分析，造成了不连续，同时概念“曲率、曲率圆及曲率半径”是注入的而不是生成的；其二，曲率公式的推导不是在原有基础上建模进行，而是另作图形处理，造成思维上的不连续；其三，从“当Δs→0时，平均弯曲程度的极限值即为点A处的弯曲程度”到“定义→曲率计算公式的推导→曲率圆与曲率半径”，仍属“定义→性质→定理→例题”的传统模式；等等.如果修改为：“①问题提出；②几何建模；③分析模型，确定目标：因为工件内表面的不同点处的弯曲程度不同，所以在不同点处所能使用的砂轮的半径也就不同，于是需要研究a）、如何计算某点处的‘弯曲程度’（在此要做‘生成性处理’，即言明：为了方便，称某点处的‘弯曲程度’为该点处的曲率）；b）、如何根据曲率确定合适的砂轮（在此要生成‘曲率圆’的概念，并获得‘所需砂轮即是最小曲率圆’的结论）；④解决问题a）：在几何模型上数学地分析曲率的意义，推出曲率的数学定义，进而推导曲率计算公式；⑤解决问题b）：分析曲率的数学定义确定曲率圆的半径，问题也就迎刃而解了”，就可较好地展现出连续的创造性思维.

6 生成性.

生成是创造的基础，也是过程哲学与意会哲学的追求，所以“过程→生成”教学必须处处体现生成，体现出创造性思维过程．首先，基本的要求是概念、定理都必须在某一过程中生成，尽力避免直接定义、直接定理的做法．其次，要体现怀特海“由多而一”、“由一而长”的创造新颖的思想，要体现波兰尼的“由‘突现’创化成的新实在”的思想．在知识的生成过程中总会面对无数种可能，其中必存在根本的、过去未有的新质，这种新质的获得就是创造，而获得这种新质就必须敢于历险、敢于超越、敢于提出猜想.教学就应模拟出这种历险、超越、猜想过程，使学生感受创造的锤炼、享受创造的喜悦，形成具有创造欲的头脑.在此猜想是更重要的，因为“没有大胆的推测，就没有伟大的发现”（牛顿），“提出一个问题往往比解决一个问题更重要”（爱因斯坦）．第三要注意教学语言的创造性，行文措辞上要选择具有生成、创造意义的词句．如“发现”、“猜想”、“得到”、“我们需要……，为了方便，根据……，给它起个名字，叫做……”等．同时还倡导“逻辑图表方法”[18]，逻辑图表具有直观性、趣味性、简单性、逻辑性、结构化特点，可提高记忆率与检索率．

6 结 语

关于过程教学、生成教学的研究较多，但是“过程→生成”并非是过程与生成的简单叠加，因为对教学而言，有过程未必有生成（无生成则无创造），有生成未必有良好的过程（没有良好的过程则可能失去良好的基础），所以强调“在过程中生成”.并且孤立地讲授“概念的发现过程”、“定理的形成过程”、“证明的思维过程”，不合“过程→生成”思想，因其缺少连续性及整体性．总之“过程→生成”教学，其过程保证了基础（知其所以然），生成保证了创造（追求所以然），并且教学过程＝学习过程＝知识生成过程（身心合一）．

笔者的教学实践证明，“过程→生成”讲授法很受学生欢迎，能有效地提高学生素质与能力，能方便地融入新型教法．当然“过程→生成”讲授法仍比传统的讲授法耗时较多，补救的办法也只有依靠适当的自学，但自学的教材也必须是“过程→生成”性教材，这样才能使学生在学习的全过程中始终沉浸在创造性的生态环境中．当然“过程→生成”讲授需要较高的讲授技巧，高兴的是我们已有大量的宝贵经验及手段可供选用（当然决不能选取注入式方法）．

本文亦是笔者从事小、中、大学教学40多年来教学感受的理性思考，难免孤见寡闻，但希能抛砖引玉，不妥之处敬请同仁斧正，更希共同关注．

[1]张莫宙．中国数学教育在改革与反思中前进[J]．数学通报，2008，47（12）：22-26．

[2]曹永听，刘华．从美国高校班级规模看我国高校大班课堂教学存在的现实意义[J]．河北大学成人教育学院学报，2006，8（2）：76-78．

[3]中国大百科全书总编辑委员会《教育》编辑委员会．中国大百科全书：教育[M]．北京：中国大百科全书出版社，1988．

[4]刘书生，董燕桥，张永泰．教学法大全[M]．北京：经济日报出版社，1990．

[5]姚诗煌，江世亮．以人为主发展大成智慧工程——钱学森先生接受本报记者采访时谈系统工程和系统科学[N]．文汇报，2001-3-20（1-2）．

[6]苗东升．把系统作为过程来对待[J]．湖南科技大学学报：社会科学版，2004，7（5）：45-50．

[7]怀特海A N．怀特海过程哲学观概要[J]．艾彦，译．世界哲学，2003（l）：2-19.

[8]迈克尔·波兰尼．科学、信仰与社会[M]．王靖华，译．南京：南京大学出版社，2004.

[9]MICHAEL POLANYI.Knowingand Being[M]．Chicago:The University of Chicago Press,1969:138.

[10]迈克尔·波兰尼．个人知识[M]．许泽民，译．贵阳：贵州人民出版社，2000：135.

[11]曲跃厚．第五届国际怀特海哲学大会在韩国召开[J]．哲学动态，2004（11）：36-37.

[12]钱振华．从宗教维度看科学发现[J]．科学技术与辩证法，2005，22（1）：17-21.

[13]杨富斌．怀特海过程哲学思想述评[J]．国外社会科学，2003（4）：75-82．19．

[14]怀特海A N．教育的目的[M]．徐汝舟，译．北京：生活·读书·新知三联书店，2002.

[15]郁振华．波兰尼的默会认识论[J]．自然辩证法研究，2001，17（8）：5-10.

[16]阿尔弗雷得·诺思·怀特海．过程与实在[M]．杨富斌．北京：中国城市出版社，2003．

[17]钱志良．论案例教学在《高等数学》教学中的重要性与可行性[J]．常州信息职业技术学院学报，2010，9（2）：50-52．

[18]王峰．逻辑图标教学法及其在高等代数教学中的尝试[J]．华中师范大学学报：自然科学版．1993（专辑）：113-121．

The Evolution of Teaching Concept：From Injection to“Process(Generation”——Based on the Teaching Discussion of Advanced Mathematics

WANG Ji-She
(Department of Mathematics and Information Technology,Hanshan Normal University,Chaozhou 521041,China)

To cultivate talents with creative ability for scientific technology,mathematics teaching plays a crucial role.The research of new teaching method is growing vigorously,nevertheless,it is difficult to put into effect in practical teaching,especially,advanced mathematics,which continues to implement the teaching procedure by“definition(nature(theorem(example”.In the long term,it will cause negative effect on our teaching,therefore,it is an important part on reforming the traditional teaching concepts.Looking forward to the development of science,to have a thorough understanding of the three dimensional objective of new curriculum reform by process philosophy,tacit philosophy and theory,the teaching concept of“process(generation”is put forward and the details are described in the passage.

process philosophy；tacit philosophy；teaching concept；concept of“process generation”

G642.0

A

1007-6883(2011)06-0099-06

2011－10－17

广东省教育科学“十一五”规划课题：基于三维目标的高师数学过程教学模式研究；项目编号：2009XM00322.

王积社（1954-），男，山省晋城人，韩山师范学院数学与信息技术系副教授.

责任编辑 朱本华