一类具有分布时滞高阶微分方程的周期解

陈仕洲

（韩山师范学院数学与信息技术系，广东潮州 521041）

一类具有分布时滞高阶微分方程的周期解

陈仕洲

（韩山师范学院数学与信息技术系，广东潮州 521041）

利用Mawhin重合度理论，研究了一类具有分布时滞的高阶p-Laplacian中立型微分方程，获得了其周期解存在性的一些新结果.

分布时滞；p-Laplacian；中立型泛函微分方程；周期解；重合度理论

1 引言及引理

近年来，关于p-Laplacian微分方程的周期解问题，已引起人们的关注[1-3]．但对具有分布时滞的高阶p-Laplacian中立型微分方程周期解的研究并不多.文[1]和[3]分别研究了具有变差变元的p-Laplacian中立型方程

2 主要结果及其证明

3 注记和例子

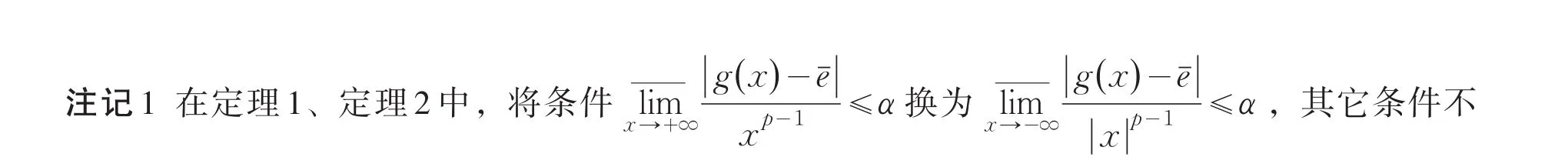
[1]彭世国.具有偏差变元的p-Laplacian中立型Lienard型方程的周期解[J]．数学年刊，2008，29A（5）：617-626.

[2]PENG SHI-GUO,ZHU SI-NING.Periodic solutions for p-Laplacian Rayleigh equations with adeviating argument[J].Nonlinear Analysis，2007，67：138-146.

[3]朱艳玲，汪凯．具有p-Laplacian算子的中立型泛函微分方程周期解[J]．系统科学与数学，2009，29（6）：808-817.

[4]LU SHIPING,GE WWIGAO,ZHENG ZUXIOU.Periodic solutions to neutral differential equation with deviating arguments[J].Appl.Math.Comput.,2004，152：17-27.

[5]GAINES R E,MAWHIN J L.Coincidence degree and nonlinear differential equations[M].Berling:Springer-Verlag，1977，95-169．

[6]LI J W，WANG G Q.Sharp inequalities for periodic functions[J]．Applied Mathematics E-Notes，2005（5）：75-83.

Periodic Solutions for a Kind of High-Order Differential Equations with Distributed Delay Arguments

CHEN Shi-zhou
（Department of Mathematics and Information Technology,Hanshan Normal University,Chaozhou 521041,China）

By using the continuation theorem of coincidence degree theory developed by Mawhin,we study a kind of high-order p-Laplacian neutral functional differential equation with distributed delay arguments.Some new results on the existence of periodic solutions are obtained.

distributed delay；p-Laplacian；neutral functional differential equation；periodic solution；coincidence degree

O175.7

A

1007-6883(2011)06-0001-07

2011-10-16

陈仕洲（1959-），男，广东汕头人，韩山师范学院数学与信息技术系副教授．

责任编辑 朱本华