Lurie时滞系统绝对稳定的时滞相关条件
2011-12-21刘轩
刘 轩
(韩山师范学院基础教育师资系,广东潮州 521041)
Lurie时滞系统绝对稳定的时滞相关条件
刘 轩
(韩山师范学院基础教育师资系,广东潮州 521041)
讨论了具有控制时滞的Lurie系统在非线性项满足有限扇形区域条件下的绝对稳定性.依据Lyapunov稳定性理论,构造一个适当的Lyapunov泛函,利用线性矩阵不等式的方法,通过一个积分不等式获得了系统绝对稳定的时滞相关条件.并应用Schur补引理将以上结果推广到了具有范数有界的不确定Lurie时滞系统,得到了系统鲁棒绝对稳定的时滞相关的充分条件.通过算例验证了本文结果的有效性.
Lurie控制系统;绝对稳定;时滞相关;线性矩阵不等式
1 引言与预备
Lurie控制系统是一类非常典型的非线性系统,其非线性项被约束在有限或无限的扇形区域内,它的绝对稳定性研究受到了许多学者的关注[1-3].2002年,冯俊涛、年晓红[4]应用Lyapunov泛函方法讨论了具有结构参数扰动和范数扰动界的不确定滞后型Lurie直接控制系统和间接控制系统的鲁棒绝对稳定性,给出了系统绝对鲁棒稳定性的充分条件.2004年,Wu[5-6]等对固定模型变换的方法进行了推广,提出自由权矩阵的的方法,得到了系统绝对稳定的时滞相关条件.2005年,陈东彦,刘伟华[7]考虑了多时滞Lurie控制系统,利用Lyapunov稳定性方法并结合Moon引理,得到了多时滞Lurie控制系统的时滞相关鲁棒稳定性判别条件.2008年,文献[8]对具有非线性干扰项的多时滞Lurie控制系统,通过一个改进的新积分不等式,给出了一个判断系统稳定的时滞相关条件.
本文利用Lyapunov-Krasovskil稳定性定理,引入了自由权矩阵,并利用了一个新的积分不等式获得了判断具有控制时滞的Lurie系统及具有范数有界的不确定Lurie时滞系统绝对稳定的时滞相关条件.这些条件均以线性矩阵不等式的形式给出,可以利用matlab工具箱进行方便求解.
引理1[7](Schur补引理)假设对称矩阵的分块可以表示为
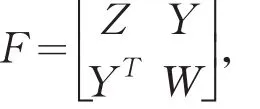
其中,Z∈Rn×n,W∈Rm×m和Y∈Rn×m,则以下两个结论等价
(1)W是非奇异的,则F>0的充分必要条件是W>0且Z-YW-1YT>0.
(2)W是非奇异的,则F>0的充分必要条件是Z>0且W-YTZ-1Y>0.
引理2[9](S-程序) 设Fi∈Rn×n, (i=0,1,2,…,p)是对称矩阵,如果存在实数τi≥0,(i=0,1,2,…,p)使得
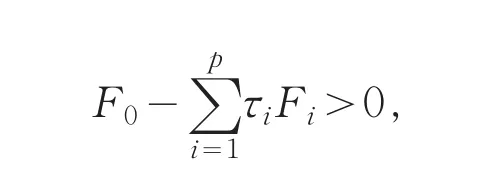
那么,对于Fi(i=0,1,2,…,p),对任意的ξ≠0,ξ∈Rn,若ξTFiξ≥0成立,则有ξTF0ξ≥0.
引理3[13]对于给定的矩阵Z(x)=ZT(x)和适当维数的矩阵H,L,如果对于任意的F满足FTF≤I,则Z+HFL+LTFTHT<0成立的充要条件是存在ε>0,使得Z+εHHT+ε-1LTL<0.
引理4[8]设x(t)为Rn上具有连续一阶导数的向量函数,则对任意的正定矩阵W∈Rn×n和任意的h>0,有下列积分不等式成立:
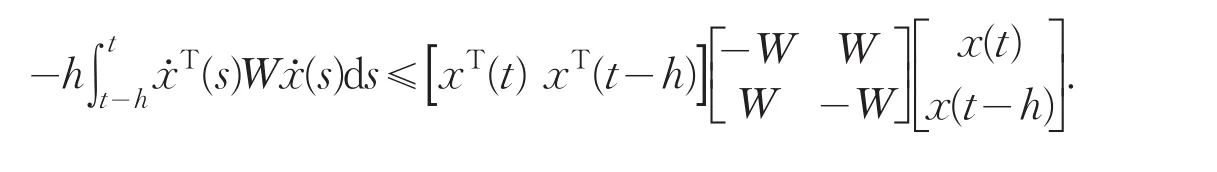
2 主要结果



3 仿真示例
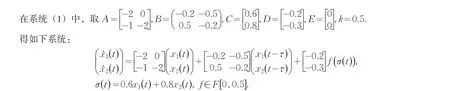
利用MATLAB解LMI(3)可得τ<0.9015,而在文献[10-12]中,该系统时滞界分别为:τ<0.3053,τ<0.3230,τ<0.7128.由于本文提高了系统稳定的时滞界,因此本文结果具有更好的有效性和较小的保守性.
[1]GAO Z X,HAN J Q.Lyapunov function of general Lurie systems with multiple nonlinearities[J].Applied Mathematics Letters,2003,16(l):119-126.
[2]GAO JIN-FENG,SU HONG-YE,JI XIAO-FU,et al.New delay-dependent absolute stability criteria for Lurie control systems[J].Acta Automatica Sinica,2008,34(10):1275-1280.
[3]王玉红,包俊东.一类非线性时滞Lurie控制系统的绝对稳定性[J].内蒙古师范大学学报,2007,36(1):30-34.
[4]冯俊涛,年晓红.不确定滞后型Lurie控制系统的鲁棒绝对稳定性-LMI方法[J].长沙铁道学院学报,2002,20(2):37-42.
[5]WU M,HE Y.Delay-dependent criteria for robust stability of time-varying delay systems[J].Automatica,2004,40(8):1435-1439.
[6]WU M,HE Y,LIU G P,et al.On absolute stability of Lurie control systems with multiple nonlinearities[J].European Journal of Control,2005,11(l):19-28.
[7]陈东彦,刘伟华.多时滞Lurie控制系统的时滞相关鲁棒稳定性[J].控制理论与应用,2005,22(3):499-502.
[8]赵峥嵘,王伟,杨斌.多时滞非线性Lurie控制系统时滞相关绝对稳定性[J].大连理工大学学报,2008,48(5):759-764.
[9]WU M,HE Y,SHE J H,et al.Robust stability for delay Lurie control systems with multiple nonlinearities[J].Journal of Computational and Applied Mathematics,2005,12(4):371-380.
[10]年晓红.Lurie控制系统绝对稳定的时滞相关条件[J].动化学报,1999,25(4):564-566.
[11]徐炳吉,廖晓昕.Lurie控制系统的时滞相关绝对稳定性判据[J].自动化学报,2002,28(2):317-320.
[12]田俊康,钟守明.具有控制时滞的滞后型Lurie控制系统的绝对稳定性判据[J].鲁东大学学报,2006,22(3):180-182.
[13]廖晓昕.稳定性的理论、方法和应用[M].武汉:华中科技大学出版社,1999:236-256.
DELAY-DEPENDENT CONDITIONS FOR THE ABSOLUTE
STABILITY OF LURIE CONTROL SYSTEMS WITH TIME DELAYS
LIU Xuan
(Department of Basic Education,Han Shan Normal University,Chaozhou 521041,china)
The absolute stability of Lurie systems with control time-delays and finite sector-bounded nonlinearity is discussed.Based on Lyapunov stability theory,by constructing a suitable Lyapunov-krasovskii functional and with linear matrix inequality(LMI)as research means,delay-dependent conditions of the absolute stability for Lurie systems are obtained by an integral inequality.Then,using Schur complement lemma,delay-dependent sufficient condition for the absolute stability of uncertain time-delays Lurie control system with norm bounded is obtained by extending above result.
Lurie control system;absolute stability;delay-dependent;linear matrix inequality(LMI)
O231.2
A
1007-6883(2011)06-0029-05
2011-09-19
刘 轩(1983-),女,辽宁本溪人,韩师师范学院基础教育师资系教师.
责任编辑 朱本华
