功能原理的价值
2011-12-21苏云
苏 云
(韩山师范学院物理与电子工程系,广东潮州 521041)
功能原理的价值
苏 云
(韩山师范学院物理与电子工程系,广东潮州 521041)
分析了功能原理演变的过程,以及演变过程中几个力学基础概念的产生和变化,进而归纳了功能原理的优势及其存在价值,阐述了“外势能”概念的引入将导致没有物理意义的结果.
功能原理;保守力;外势能
长期以来,在一些经典力学的教科书和文献中,围绕着功能原理和机械能守恒定律等内容存在一些争论和分歧.问题一,功能原理是否有存在的必要,这涉及几个基础概念的引入和定义,以及功能关系和机械能守恒定律.问题二,引入外势能概念的必要性,结果不但使功能原理和机械能守恒定律出现了两种表述,还涉及到所研究的力学系统的稳定性问题.
经典力学是物理学的入门篇章,它为物理学乃至整个自然科学提供了许多非常重要的基础概念.然而时至今日,在这一基础学科中却仍然存在上述悬而未决的争议和混乱,已经给相关内容的教学带来了不小的负面影响,澄清这些问题对经典力学以及其他学科来说都有重要的意义.
1 关于功能原理的存废
有学者认为质点系的功能原理造成了一些混乱,也不符合国际惯例,所以应该废除[1].鉴于国内许多经典力学教科书都包含功能原理的内容,因此上述观点给力学教学界造成了不小的影响,为了澄清这个问题,回顾一下这个原理的来龙去脉,与国际惯例做个比较,进而判断其存在的价值.
从牛顿第二定律出发可以推导出质点系的动能定理:

经典力学的常用力中只有重力、引力和弹性力具有已知的函数形式,它们分别由万有引力定律和胡克定律来表述.在得到动能定理之后,将这些已知的力函数代入方程(1)作一番演算是物理学原始探究的典型思路.为简单起见,先考虑系统内的质点仅受重力作用的情况,将重力做的功代入(1)式左端可得
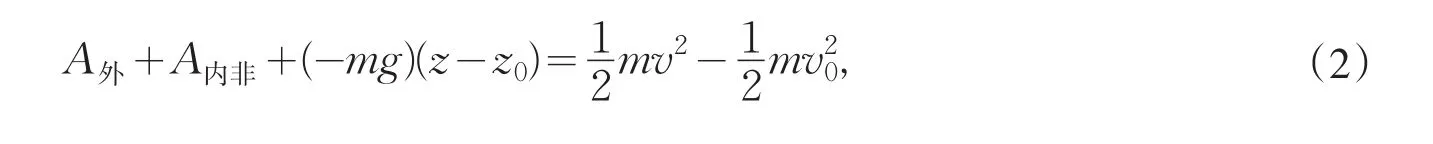
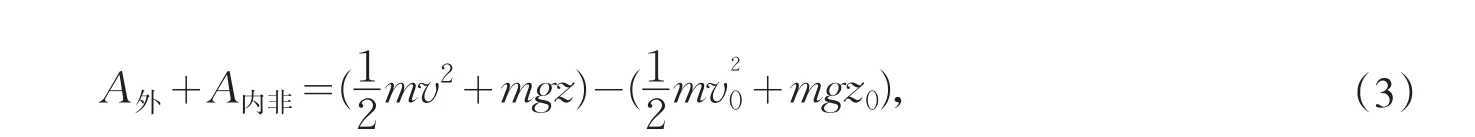
接下来分别讨论引力和弹性力的情况,只需将mgz分别换成-GMm/r和kx2/2即可得到两组与(2)和(3)类似的方程.对系统内所有质点归纳这三组方程就可以得到:

这就是国内许多教材所称的质点系的功能原理[2].当A外和A内非都等于零时,就得到系统的机械能守恒定律.
上述的推导过程看似简单,却蕴含了非常丰富的内容:
①从(2)式可知,当质点运动了一个闭合路径时,重力所做的功等于零,说明它所做的功与质点运动的路径无关,引力和弹性力也有相同的情况,这一特性最终导致保守力概念的产生.随后在保守力的基础上出现了几个新的物理量mgz、-G Mm/r和kx2/2,被定义为相应保守力的势能,进而得到了机械能的概念.
经典力学正是在也只有在上述推导过程中才体现出引入并严格定义这三个新物理概念的必要性,因此上述的演变符合物理概念的形成、发展和演变的过程,也符合人们认识自然的规律.如果丢掉了功能原理,也就丢掉了这些概念的来龙去脉,不利于人们更好地理解和认识这些概念.
值得注意的是,教科书是在推导功能原理之前先单独定义保守力和势能,再用它们来解释随后推导出来的功能原理,这种做法把上述概念的演变过程完全剔除掉了,不利于理解上述概念的来龙去脉.
②方程(2)左端重力功前面的那个负号似乎是为移项做准备的一种数学技巧,但在定义保守力和势能概念的时候,这个负号成为保守力的功与势能关系中不可缺少的一部分,于是国内外的力学教科书中便有了“保守力做的功等于势能增量的负值”的说法,遗憾的是教科书都未对这个负号给予必要的说明,给相关概念的理解造成了一些困难.当本文推导出方程(3)的时候,这个问题便迎刃而解了.
③上述推导过程揭示了保守力概念在功能转换过程中的一种独特性质,它要么以力做功的形式存在,成为改变质点动能或机械能的原因,要么以势能的形式呈现,被其他力做的功所改变,二者必居其一.在解决问题时如果侧重保守力所做的功,就应该保留在方程(2)的左端,体现其改变系统能量的作用.如果侧重它的能量属性,就要将它的功转换成势能,移项到方程右端组成系统的机械能,并被其他力做的功所改变.究竟采取哪种形式取决于变换后的结果是否有物理意义,以及解决实际问题的方便.
④方程(4)的功能原理系统地建立了做功与机械能改变的一般关系,进而得到了机械能守恒的数学条件.一般来说,教科书在推导功能原理的时候仅仅强调这一点.
国外(主要是英语国家)的许多力学教材并不推导出功能原理的结果,而只推导出动能定理的(1)式,而且也是事先单独地定义保守力和势能等基础概念,再用一种类似于习题演算的方法直接推导出机械能守恒的结论.[3]由于没有功能原理,因而也没有得出做功与机械能改变的一般关系,以及机械能守恒的普遍数学条件,对保守力的功与势能增量之间的那个负号也未作任何解释.
综上所述,众多力学概念的引入和定义、关键负号的解释、功能关系的建立、守恒的普适条件等等,这一切充分体现了功能原理的价值,也突显出与上述国际惯例相比的明显优势,因此完全应该保留.
2 关于外势能的问题
方程(4)是将质点系内力的功按照保守力进行拆分所得的结果,那么外力的功是否也应该按同样方式进行处理呢?前面在讨论保守力的特性时曾说到,保守力的作用效果是以做功还是能量形式呈现,取决于结果是否有物理意义.这可以用来确定引入外势能概念是否有意义.
为了简化讨论,只考虑质点系的外力所作的功,把其中保守力的成分拆分出来,转换成外势能增量的负值,然后再移项,于是方程(1)渐次变为:
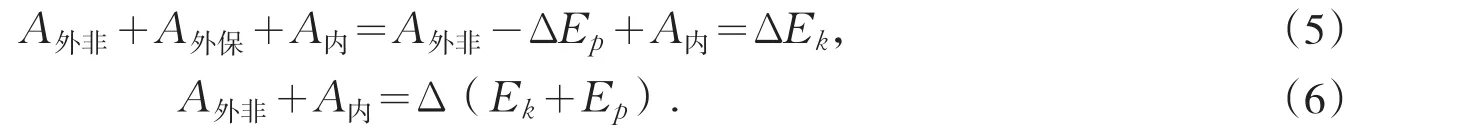
表面上看,引入外势能后的结果与方程(1)到(4)的变化是一样的,然而却隐藏着一个致命的错误.
方程(4)的右端是一个有限的质点系的动能、势能或机械能,左端是该系统所受外力及非保守内力所做的功,由此推论的机械能守恒也是针对这个系统而言的.整个方程都是围绕着这个有限且不变的质点系统来讨论的,物理意义非常清晰.
当变换到方程(6)的时候出现了一系列的问题:方程左端的功是针对哪个质点系统的,右端的动能、势能和机械能又属于哪个质点系呢?
外力中的保守力就是系统外某质点作用在该系统内某质点上的力,如果把它的功转换成外势能,再移项组成机械能,就必须把系统外的那个施力质点也纳入到预先设定的质点系中来,因为势能属于这一对保守力所对应的那两个质点.否则就会出现一个质点在系统内,另一个却在系统外的情况,造成势能和机械能归属的混乱.因此,当方程(5)中的外势能差被移项时,就不得不把系统外的那个施力质点也纳入到预先设定的系统中来.
然而万有引力定律告诉我们,宇宙万物都与该系统内的每一个质点至少有保守的引力相互作用,那就不得不将系统外的所有质点都纳入到所研究的系统中来.这样一来,方程(6)所对应的系统实际上是整个宇宙,相应的功、动能、势能和机械能都是针对这个宇宙而言的,而不再是方程(4)所对应的那个有限的不变的系统了.按照这种逻辑,在研究任一质点或有限系统的功能关系时,都不得不把整个宇宙纳入到研究对象中来.显然,这是物理学所不能接受的.
与此相反,对系统内保守力的上述操作却不会改变预先设定的研究系统,因此可以根据研究的需要来选择如何呈现内保守力的作用效果,做功或者势能.
综上所述,外势能并不是一个新概念,而只是始于方程(1)的一种可能的操作,在数学上虽然并无不妥,但却无法得出任何有物理意义的结果,反而干扰和破坏了对功能关系物理本质的认识,说明这个外势能概念没有意义.
[1]喀兴林.编者的话[J].大学物理,2000,19(2):29.
[2]程守洙,江之永.普通物理学(第五版第一册)[M].北京:高等教育出版社,2000:79-116.
[3]FISHBANE PAUL,GASIOROWICZ STEPHEN,THORNTON STEPHEN.Physics For Scientists And Engineers[M].3rd ed.New Jersey:Pearson Prentice Hall,2005:186.
On the Value of Principle of Work and Energy
SU Yun
(Department of Physics and Electronic Engineering,Hanshan Normal University,Chaozhou 521041,China)
The advantage and value of work-energy theorem are analyzed,so are the basic concepts of classical mechanics,and the external potential energy is clarified as a useless concept.
principle of work and energy;conservative force;external potential energy
O313.2
A
1007-6883(2011)06-0046-03
2011-06-01
苏 云(1957-),男,内蒙古呼和浩特人,韩山师范学院物理与电子工程系副教授.
责任编辑 朱本华
