V型原子介质中周期量级脉冲激光传输特性对载波包络相位的依赖性＊

谭 霞，张成强

（1.潍坊学院，山东 潍坊 261061；2.齐鲁师范学院，山东 济南 250013）

V型原子介质中周期量级脉冲激光传输特性对载波包络相位的依赖性＊

谭 霞1，张成强2

（1.潍坊学院，山东 潍坊 261061；2.齐鲁师范学院，山东 济南 250013）

通过求解Maxwell－Bloch方程，研究了稠密的V型三能级原子介质中，载波包络相位（CEP）ø对周期量级脉冲激光的传输特性及频谱特性的影响。结果表明：对于大面积的脉冲，周期量级激光脉冲的载波和相应的光谱对CEP具有很强的敏感性。CEP的大小可以影响脉冲振幅大小、传播速度快慢及脉冲的分裂。另外，其它条件一定CEP不同时，由于相干效应的不同，脉冲频谱受到CEP的影响，但不足以引起高频成分的显著变化。当ø＝0时，可得到频谱更宽、连续性更好的超连续谱。

周期量级脉冲激光；Maxwell－Bloch方程；近偶极—偶极相互作用

1 引言

近年来，随着周期量级飞秒激光脉冲［1－5］的不断产生，超短脉冲的载波及包络之间的相对相位（Relative Carrier－Envelope Phase，RCEP；实际上对单脉冲来说就是绝对相位）漂移就成了不容忽视的问题。单色超短脉冲的载波包络相位（CEP）对很多非线性过程，例如谐波产生、原子离化、终态能级布居数和阿秒脉冲的产生具有重要的控制作用［1］。首先提出几周期脉冲绝对相位并予以讨论的Xu L等［6］在实验中发现锁模激光器产生的脉冲串中，载波相对于包络的位置是迅速变化的。相邻脉冲的相位之所以不同，其根本原因就在于包络以群速度传播而相位却以相速度推进，于是使得脉冲串的载波在包络之下滑动。因此，载波相位ø的存在几乎是不可避免的，即使是稳定运行的锁模激光器也不能使ø保持为零。

当考虑两个超短脉冲组合时，两个脉冲间发生相干作用，两个脉冲的相对载波包络相位（RCEP）也应该会对脉冲在介质中的传播特性和光谱特性产生重要影响。夏可玉等［7］研究表明，双色脉冲在二能级介质中传播时，调整RCEP可导致偶次谐波的建立和分裂。宋晓红等［8］研究了二能级原子介质中的双色场光谱特性，发现即使是小面积超短脉冲激光也可以因两脉冲间的干涉效应而使得高频成分产生，相应的光谱强烈地依赖于两个激光脉冲间的RCEP。Loiko Y等［9］模拟了在二能级系统中双色脉冲通过RCEP控制自感应透明现象，而且研究了双色脉冲在三能级∧系统中传播时相敏频率下的转换现象。

但以上关于超短脉冲CEP控制作用的研究主要涉及到二能级系统，对三能级系统的研究也只是涉及到∧型结构。而三能级系统是最重要最具有代表性的能级系统，进行三能级不同类型系统中双色超短脉冲CEP控制作用的研究是十分必要的，因为周期量级激光脉冲在三能级不同类型系统中传播规律的研究具有非常重要的理论和实际意义［10－13］。本文通过求解Maxwell－Bloch方程，研究了不同的载波包络相位的入射脉冲在V型三能原子介质中的传播，发现脉冲的传播特性和光谱特性对CEP有较强的依赖性。

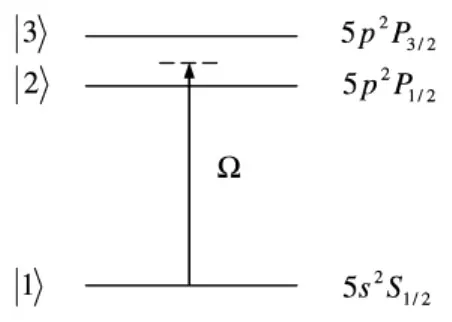
图1 V型三能级Rb原子的能级结构

2 理论模型

图1给出了Rb原子的能级结构，｜1〉，｜2〉，｜3〉能级分别代表铷原子的5s2S1／2，5p2p1／2和5p2p3／2能级。

根据刘维尔方程可以得到系统的密度矩阵方程：

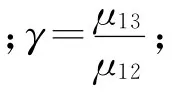
当介质的原子密度很大时，就要考虑NDD相互作用，此时微观局域场可写为［14］

其中，ε0是真空电容率，Px是宏观极化强度。设电场¯E沿x方向极化、磁场¯H沿y方向极化，Maxwell方程写为

考虑到NDD相互作用和耗散效应，并采用如下代换

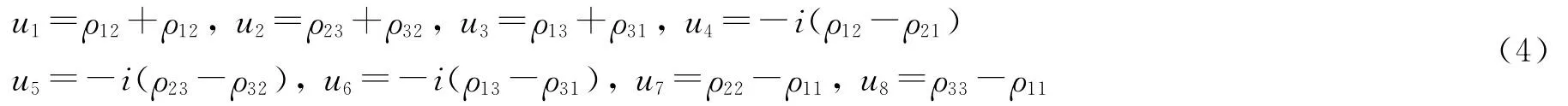
若初始条件取为ρ11＝1，其余ρij＝0（i，j＝1，2，3），则系统密度矩阵的实数形式即系统的一维Bloch方程可表示为

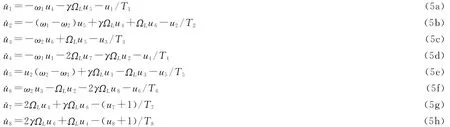
为了研究各能级粒子数布居的演化特性，采用PC和FDTD法数值求解Maxwell方程（3）和Bloch方程（5）。设初始入射脉冲为双曲正割型脉冲

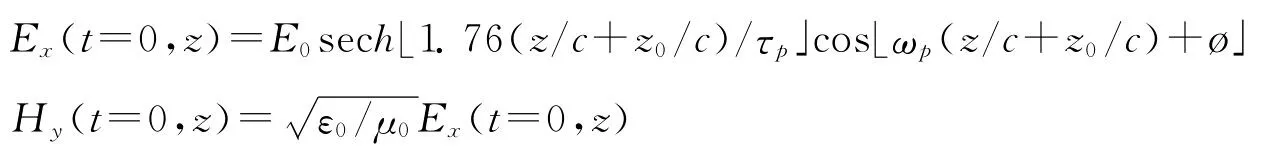
式中，E0是初始入射的脉冲包络的最大值，τp为脉冲宽度。脉冲和介质的参数取为ω1＝2.37fs－1，ω1＝2.42fs－1，ωp＝2.395fs－1，τp＝5fs，μ12＝1.48×10－29Asm，μ13＝2.09×10－29Asm。ø为脉冲的载波包络相位，分别选ø＝0π和ø＝0.5π，粒子数密度为N＝6×1025m－3。对于飞秒量级超短脉冲激光，脉冲宽度远小于各密度矩阵元的驰豫时间，因此在计算过程中各密度矩阵元的衰减速率取相同值，即1／Tm＝1× 1010s－1，m＝1，2，…，8。

3 数值计算结果及分析

3.1 有效面积为2π的脉冲对相位的依赖性

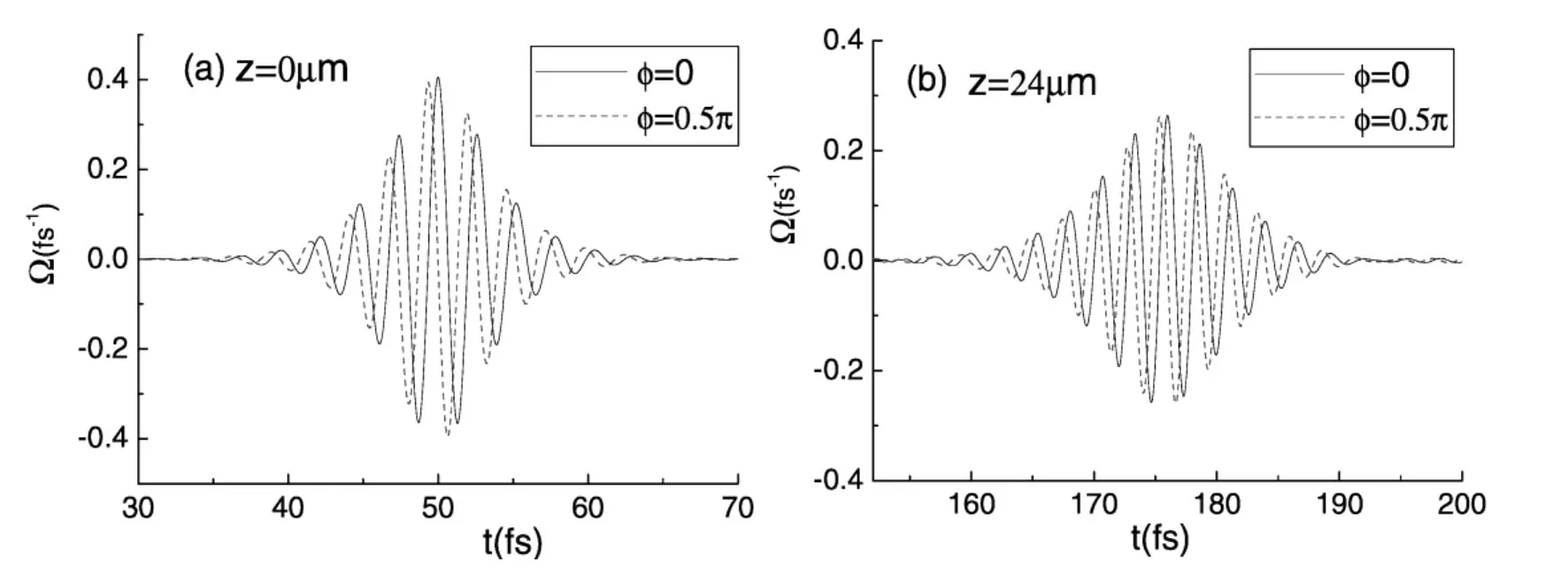
图2 相位分别为ø＝0π（实线）和ø＝0.5π（虚线）时，1.1547π脉冲载波拉比频率随时间的演化（脉冲传播距离分别为（a）：z＝0μm；（b）：z＝24μm）

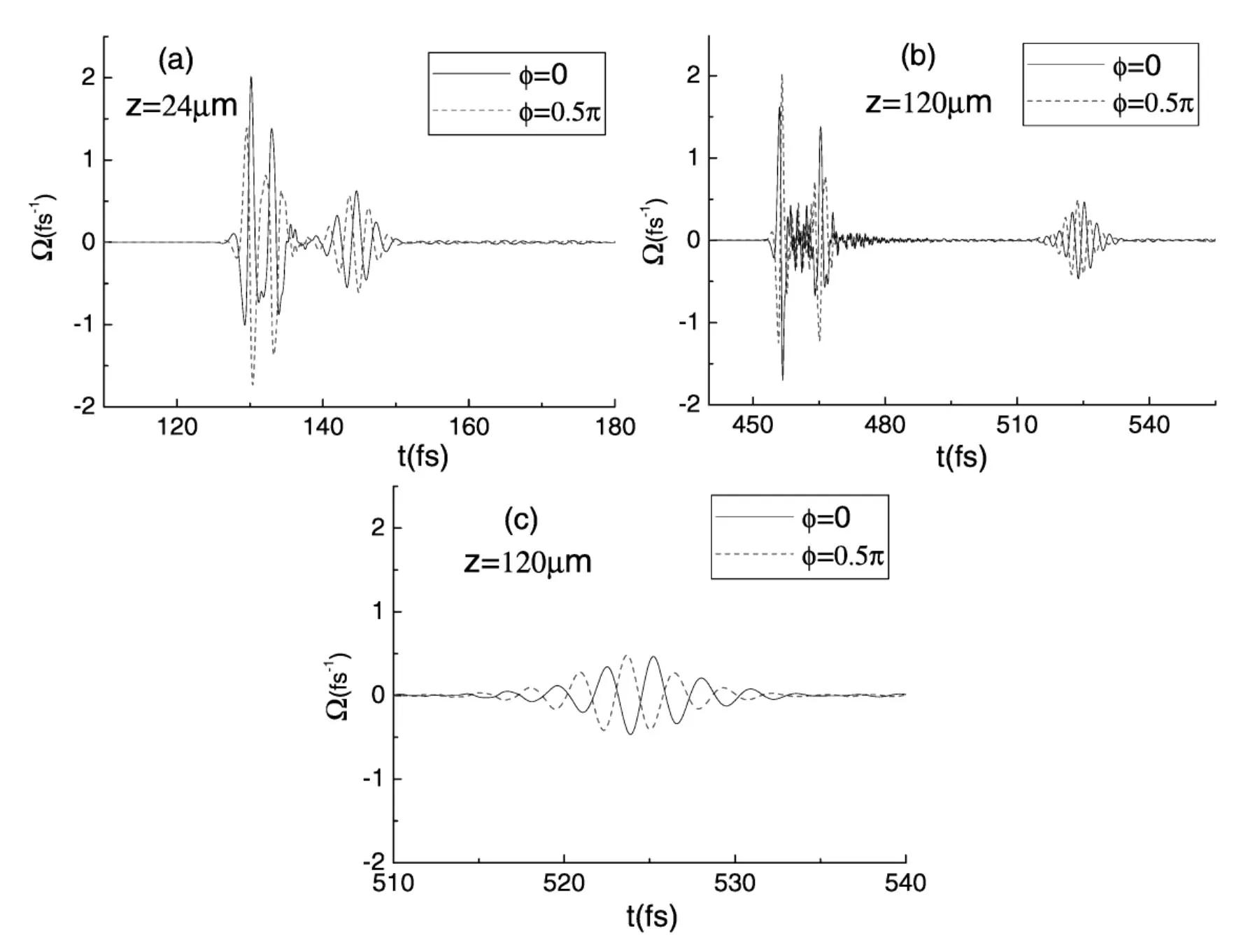
图3 相位分别为ø＝0π（实线）和ø＝0.5π（虚线）时，4π脉冲载波拉比频率随时间的演化（脉冲传播距离分别为z＝24μm（a），z＝120μm（b）和z＝120μm（c））

首先模拟初始脉冲面积为A＝1.1547π，对应有效脉冲面积为2π的周期量级超短激光脉冲对CEP的依赖性，结果如图2所示。图2显示了相位ø＝0π和ø＝0.5π的脉冲分别在z＝0μm和z＝24μm处的载波拉比频率。图2（a）表明CEP不同的脉冲其载波强度有很大的差别，当ø＝0π的脉冲到达电场的最大值时，ø＝0.5π的脉冲正好处于电场的零值处。而且，ø＝0π的电场分布是对称的，而ø＝0.5π的电场分布是不对称的。在z＝24μm处，相位不同时载波拉比频率的强度也有类似的差别，如图2（a）所示。由于粒子数密度为N＝6×1025m－3时，较强的自相位调制作用，两种情况下，脉冲振幅变小，脉宽变大，两脉冲均被展宽。此时，两种情况下脉冲的相位差仍为0.5π，两个脉冲具有不同的光强。

3.2 4π脉冲对相位的依赖性

图3描述了相位为ø＝0π和ø＝0.5π时，4π脉冲传播到24μm和120μm处，载波拉比频率随时间的演化。由图3（a）可以看出，z＝24μm处，4π脉冲分裂出一个子脉冲。对于主脉冲，两个不同相位的载波拉比频率的最大值有所不同，因此，两个脉冲的强度不同，从而引起不同的调制效应，两者发生了不同的形变；传播过程中，两者的相位差不再是0.5π，而是在脉冲的前沿小于0.5π，在脉冲的后沿大于0.5π，这就说明分裂出的子脉冲的相位差要大于0.5π，图3（a）中两者子脉冲的演化特性也清楚的反应出这一点。随着传播距离的增大，载波的形变导致脉冲不再是入射时的正弦（或余弦）函数，脉冲传播对相位的依赖性更加明显。图3（c）是图3（b）中第二个子脉冲的放大图。CEP不同的两脉冲此时的相位差接近，这说明分裂子脉冲对脉冲的依赖性更加显著。

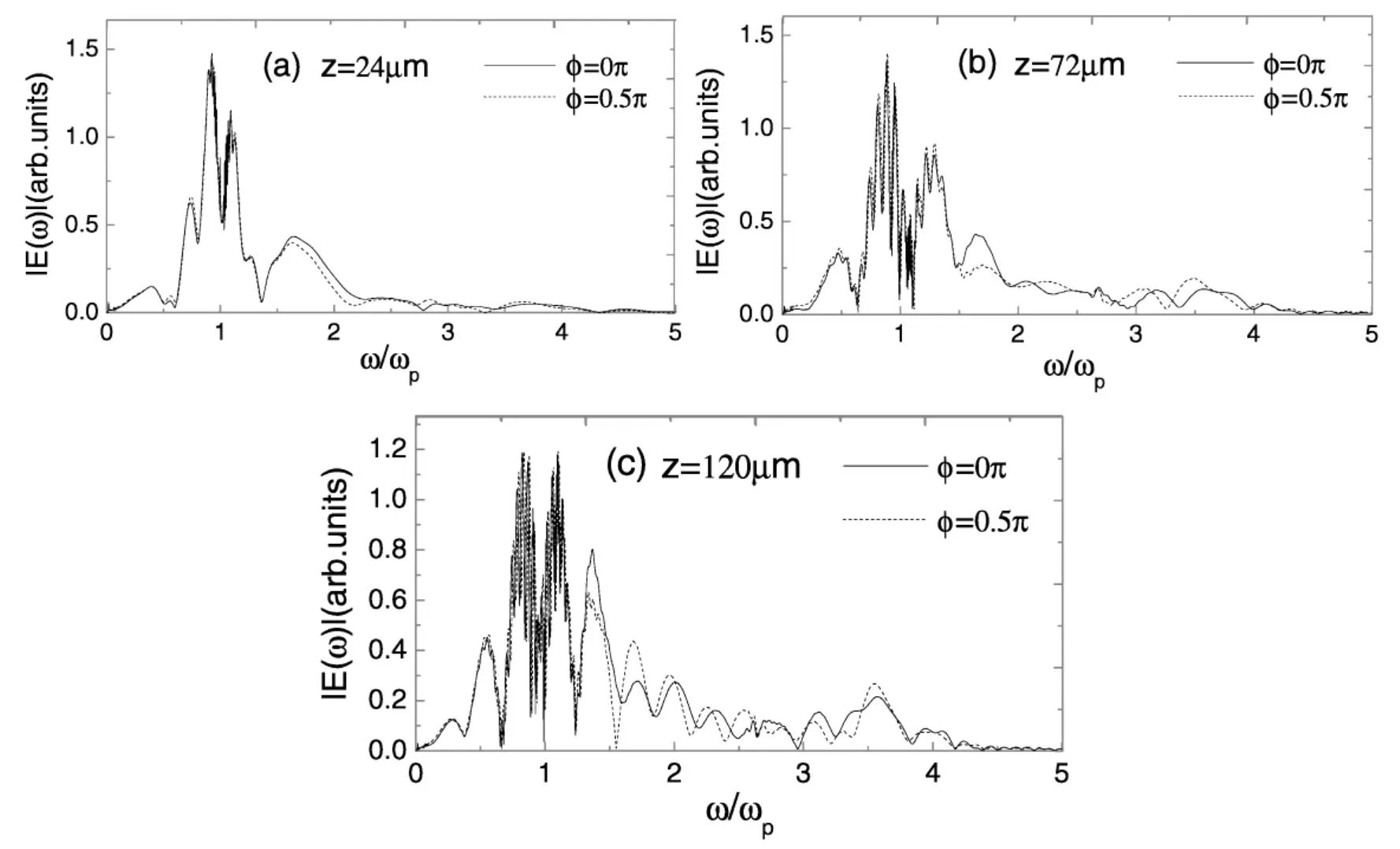
图4 相位分别为ø＝0π（实线）和ø＝0.5π（虚线）时，4π脉冲的频谱图（脉冲传播距离分别为（a）：z＝24μm；（b）z＝72μm；（c）：z＝120μm）

既然相位不同时脉冲发生了不同的载波调制，具有不同的形变，相应的频谱也表现出不同的特性。图4给出了相位分别为ø＝0π和ø＝0.5π时，4π脉冲传播到24、72、120μm处的频谱图。对于同一相位，由图4中可以看出，首先，共振频率附近，光谱表现出振荡特性，随着传播距离的增加，这种振荡特性表现的更加明显，可以推想，这是由于具有振荡处频率的脉冲之间的相干作用产生的；其次，随着传播距离的增加，光谱的振幅略有减小，这是由于脉冲被展宽，振幅减小引起的。

另外，对于4π脉冲，由于脉冲较强的自相位调制的作用，光谱展宽，出现明显的高频成分，并且随着传播距离的增加，高频成分振幅增大，出现较为显著的连续波。

对于不同的相位，频谱的高频成分区别较为明显，ø＝0.5π时高频成分的连续性比ø＝0π时较好。高频成分比较均匀，呈现良好的平坦性。平坦性是连续谱的重要特性之一，它有利于频谱的实际应用。

连续谱的产生是有场强阈值的，只有当电场强度增加到一定程度时，连续谱才能形成。这一结论已经被实验所证实。另外，连续谱的产生还有赖于脉冲的传播距离。随着传播距离的增大，高频成分会逐渐增多，从而形成连续谱。共振频率附近的振荡特性与脉冲的延迟时间有关，随着延迟时间的增大，振荡的越来越强烈。振荡特性与脉宽也有很大的关系，见图5。

图5描述了脉宽不同时，初始脉冲面积为A＝2.31π，对应有效脉冲面积为4π的周期量级超短激光脉冲的光谱特性。由图5（a）和（c）可以看出，脉冲面积一定，脉宽较大时，载波拉比频率的振荡周期越多，脉冲较容易发生分裂。由图5（b）和（d）可以看出，脉宽较大时，共振频率附近的振荡较为强烈，脉宽较小时，频谱中的高频成分比较显著。对图4（a）和5（b）进行比较可以看出，脉宽一定，4π脉冲的高频成分较为显著。2.31π脉冲的振荡周期较多，共振频率附近的振荡较为强烈，见图3（a）和5（a）。

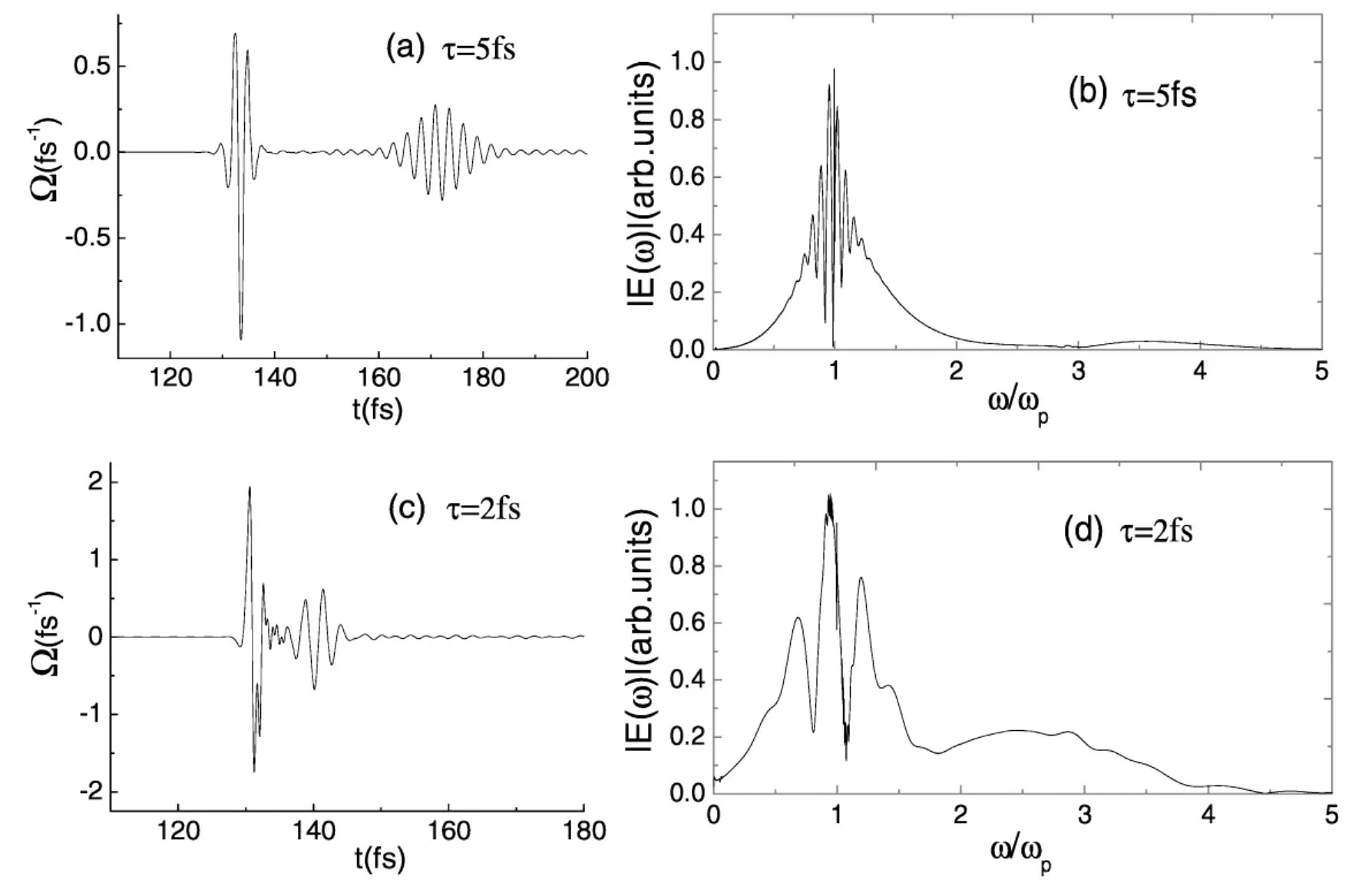
图5 脉宽分别为2fs和5fs的2.31π脉冲的载波拉比频率及其频谱图（相位ø＝0.5π，脉冲传播距离为z＝24μm）

3.3 6π脉冲对相位的依赖性

增大入射脉冲的面积到6π，相位效应会进一步增强。如图6所示，不同CEP的脉冲它们的形变彼此十分不同，而且脉冲的分裂位置也有很大的差别。显示了明显的相位依赖性，这是因为脉冲强度增大，载波效应增强的缘故。由图6（a）所示，分裂小脉冲的传播距离显著不同，与ø＝0π时相比，ø＝0.5π时脉冲的传播发生了延迟现象，随着传播距离的增大，延迟现象更加明显，见图6（b）。主脉冲的相位也有显著的差别。

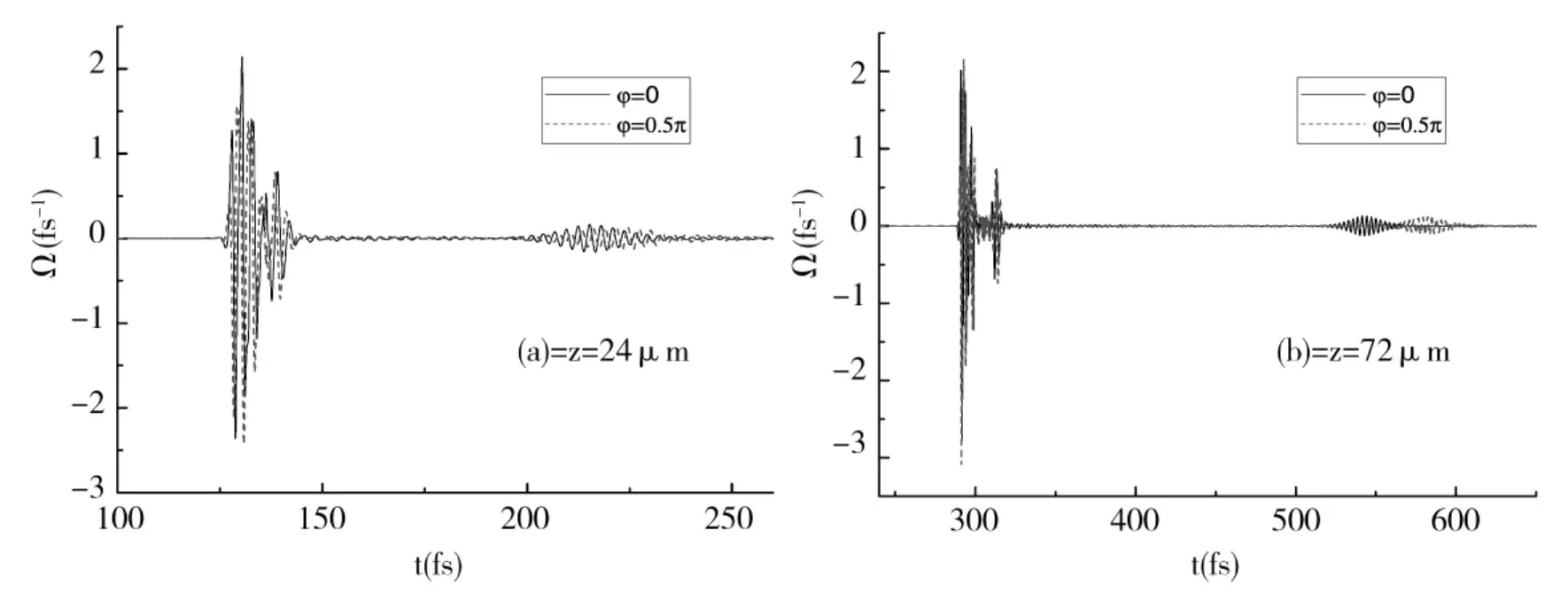
图6 相位分别为ø＝0π（实线）和ø＝0.5π（虚线）时，6π脉冲载波拉比频率随时间的演化（脉冲传播距离分别为（a）：z＝24μm；（b）：z＝72μm）

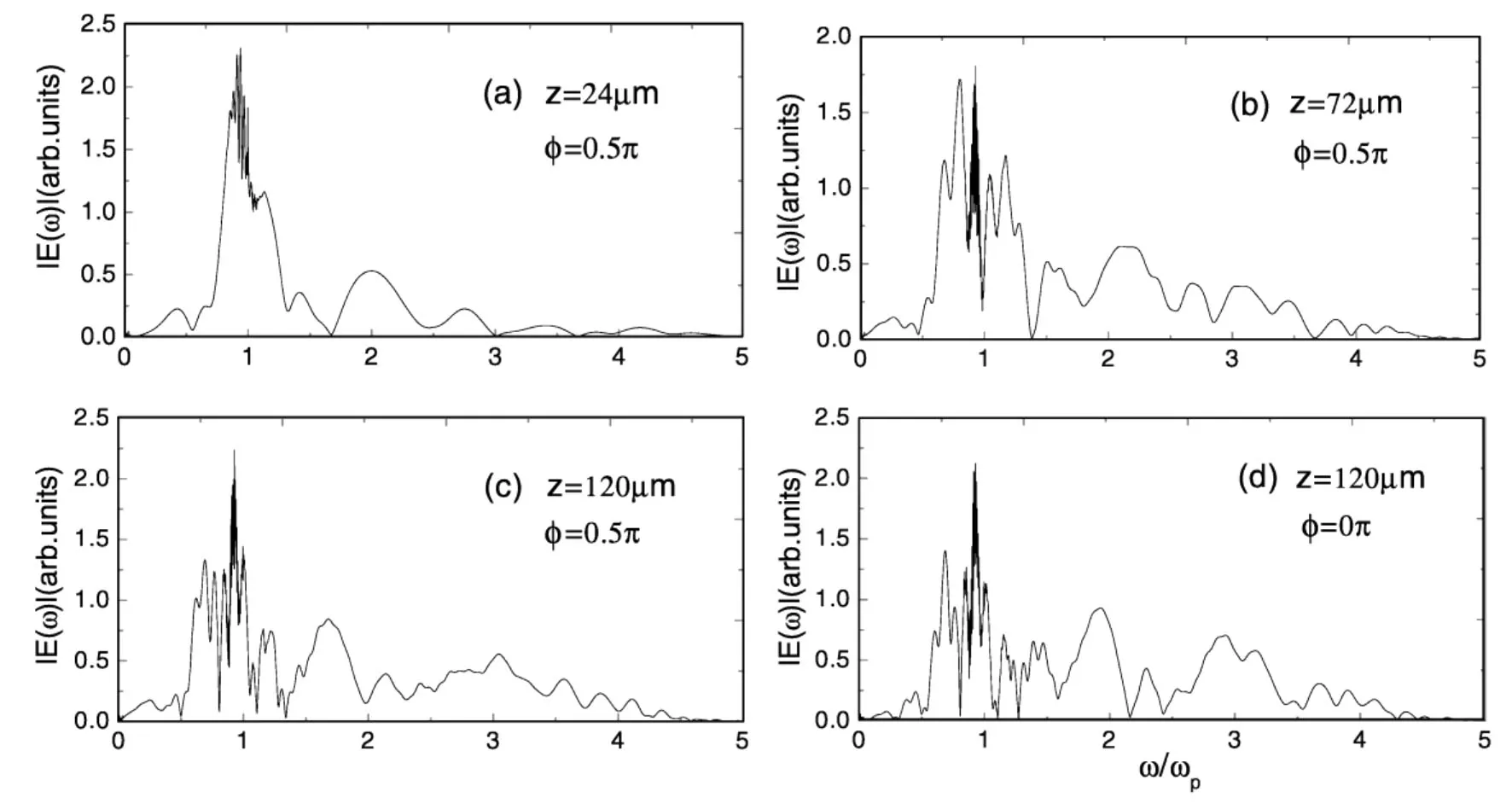
图7 相位分别为ø＝0π和时ø＝0.5π，6π脉冲的频谱图（（a）：z＝24μm；（b）：z＝72μm；（c）：z＝120μm；（d）：z＝120μm）

图7给出了不同传播距离处，两个相位分别为ø＝0π和ø＝0.5π的6π脉冲的频谱图。由图7（a）－（c）可以看出，随着传播距离的增大，频谱的振荡特性更加明显，高频成分更加显著，这与脉冲面积为4π时的结论一致。但6π脉冲频谱的振幅大于4π脉冲频谱的振幅，高频成分更加显著。对图7（c）和（d）进行比较也可以看出，ø＝0.5π时脉冲频谱高频成分比较均匀，呈现良好的平坦性。

4 结论

通过数值模拟具有不同载波包络相位（CEP）的周期量级激光脉冲在V型三能原子介质中的传播，结果表明，由于强的自相位调制作用，周期量级激光脉冲的载波和相应的光谱对CEP具有很强的敏感性。有效脉冲面积为2π的脉冲的传播对CEP的依赖性较弱。对于大面积的脉冲，载波拉比振荡对CEP的敏感性起了更重要的作用。分裂子脉冲的相位差要大于主脉冲的相位差，子脉冲的传播距离显著不同，与ø＝0π时相比，ø＝0.5π时脉冲的传播发生了延迟现象，随着传播距离的增大，延迟现象更加明显。

CEP不同时，脉冲的频谱都出现振荡特性，随着传播距离的增加，这种振荡特性表现的更加明显。对于大面积脉冲，频谱中出现高频成分，高频成分的振幅随着传播距离的增大而增大，出现较为显著的连续波。脉冲面积一定，脉宽较大时，脉冲较容易发生分裂，且共振频率附近的振荡较为强烈。脉宽较小时，脉冲频谱中的高频成分比较显著。ø＝0.5π时频谱中高频成分的连续性比ø＝0π时好，高频成分比较均匀，呈现良好的平坦性。

［1］Brabec T，Krausz F.Intense few－cycle laser fields：Frontiers of nonlinear optics［J］.Rev Modern Phys，2000，72（2）：545－591.

［2］Persson E，Schiessl K，Scrinzi A，et al.Generation of attosecond unidirectional half-cycle pulses：Inclusion of propagation effects［J］.Phys Rev A，2006，74（1）：13818－13825.

［3］Leblond H，Sazonov S V，Mel’nikov I V，et al.Few－cycle nonlinear optics of multicomponent media［J］.Phys Rev A，2006，74（6）：63815－63822.

［4］Krausz F，Ivanov M.Attosecond physics［J］.Rev Mod Phys，2009，81（1）：163－234.

［5］Silaev A A，Vvedenskii N V.Residual－current excitation in plasmas produced by few－cycle laser pulses［J］.Phys Rev Lett，2009，102（11）：115005－115009.

［6］Xu L，Spielmann C，Poppe A，et al.Route to phase control of ultrashort light pulses［J］.Optics Letters，1996，21（24）：2008－2010.

［7］Xia K Y，Niu Y P，Li C F，et al.Absolute phase control of spectra effects in a two－level medium driven by two－color ultrashort laser pulses［J］.Phy Lett A，2007，361（1）：173－177.

［8］Song X H，Gong S Q，Jin S Q，et al.Formation of higher spectral components in a two－level medium driven by two－color ultrashort laser pulses［J］.Phys Rev A，2004，69（1）：15801－15804.

［9］Loiko Y，Serrat1 C.Coherent and phase sensitive phenomena of ultrashort laser pulses propagating in three－levelΛ－type systems studied with the finite－difference time－domain method［J］.Phys Rev A，2006，73（6）：63809－63819.

［10］Chin S L，Hosseini S A，Liu W，et al.The propagation of powerful femtosecond laser pulses in optical media：physics，applifications and new challenges［J］.Can J Phys，2005，83（9）：863－905.

［11］Tan X，Fan X J，Yang Y L，et al.Time evolution of few－cycle pulse in a dense V－type three－level medium［J］.Journal of modern optics，2008，55（15）：2439－2448.

［12］Tan X，Yang Y L，Tong D M，et al.Effect of the ratio of transition dipole moments on few－cycle pulse propagation［J］.Chinese Optics Letters，2008，6（8）：607－610.

［13］Tan X，Wang Z D，Wang L，et al.Relative carrier－envelope phase dependence of two－color ultrashort laser pulses propagation in a V－type three－level atomic medium［J］.Chinese Physics B，2010，19（6）：64211－64217.

［14］Bowden C M，Dowling J P.Near dipole－dipole effects in dense media：generalized maxwell－bloch equations［J］.Phys Rev A，1993，47（2）：1247－1251.

（责任编辑：刘乃生）

Effects of Carrier－envelope Phase on Few－cycle Ultrashort Laser Pulses Propagation in V－type Medium

TAN Xia1，ZHANG Cheng－qiang2
（1.Weifang University，Weifang 261061，China；2.Qilu Normal University，Jinan 250200，China）

By solving the full Maxwell－Bloch equations，the effects of the carrier－envelope phase（CEP）on pulse propagating and spectra characteristics of few－cycle ultra short laser pulses in a dense V type three－level atomic medium are investigated.The results show that the carrier propagation and spectrum evolution of the pulse are sensitive to its CEP and the phase sensitivity is more obvious for larger area pulse.The CEP can affect the amplitude，propagating velocity and pulse splitting case.Moreover，under the same condition，the pulse spectra are affected by the initial carrier－envelope phases due to the different coherence effect，which don’t induce obvious changes of higher spectral components.When，the super continuum with wider spectral range and better continuity of high frequency components can be obtained.

few－cycle laser pulse，Maxwell－Bloch equations，near dipole－dipole interaction

2011－05－16

谭霞（1980－），女，山东泰安人，潍坊学院物理与电子科学学院讲师，博士。研究方向：激光与物质相互作用。

O437 文献标识码：A 文章编号：1671－4288（2011）06－0031－07