精确行波解的构造及其应用＊

冯滨鲁

（潍坊学院，山东 潍坊 261061）

精确行波解的构造及其应用＊

冯滨鲁

（潍坊学院，山东 潍坊 261061）

通过利用修正里卡蒂方程得到一个构造精确行波解的方法，并且举出例子来展现这一方法在处理非线性波方程上的应用。

构造；行波解；Kdv方程

1 引言

非线性物理现象同非线性偏微分方程（NLPDEs）紧密相联，并且涉及到许多其他领域，如生物、化学、力学等等。作为这些现象的数学模型，NLPDEs的精确解的研究将帮助我们更好地理解这些现象，所以许多学者研究找到了多种方法来求精确解，如反散射方法［5－6］、hirota双线性方法［7－9］、tanh方法［10－12］、齐次平衡法等。本文通过利用修正里卡蒂方程获得一个构造精确行波解的新方法，并且举出例子来展现这一方法在处理非线性波方程上的有效应用。

2 主要结果

对于非线性方程

其中，P是一个关于u和u的各阶偏导数的一个多项式，为得到方程（1）的行波解，作如下变换

这里，k，w为待定常数，ξ0为任意常数。

那么方程（1）就变成一个常微分方程

假设方程有如下形式的解

由文献［1］知Y满足下面的方程

其中，m和r是整数，ci（i＝1，2，…，r）是待定常数，m和r的关系可通过平衡最高阶导数项和非线性项得到。如果m不是一个整数，则可通过相应的变换公式［1］来解决。然后将方程（3）代入常微分方程（2）并使用方程（4）得到一个关于Y的各次幂的一个代数方程，因为Y的各次幂系数都为零，从而得到一个关于k，c，a0，…，an，b1…bn的方程组。利用Mathematica或者Maple就可将它们解出来，最后只需将上面的结果代入到方程（3）便得到方程（1）的解。

从上面的讨论，可以看出如何确定或解出方程（4）的更多形式的解是关键。范［1］已经给出当r＝3或r＝4的5种形式的解，本文将讨论r＝2，3，4时更一般的解。首先将方程（4）记成下面的形式

情形（Ⅰ） r＝2，即Y′2＝A＋BY＋CY2

如果B＝0，则

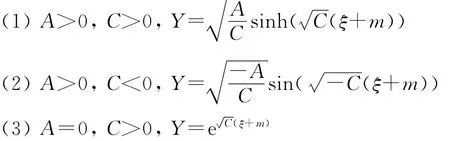
其中，m是积分常数。

如果B≠0，根据文献［1］，则

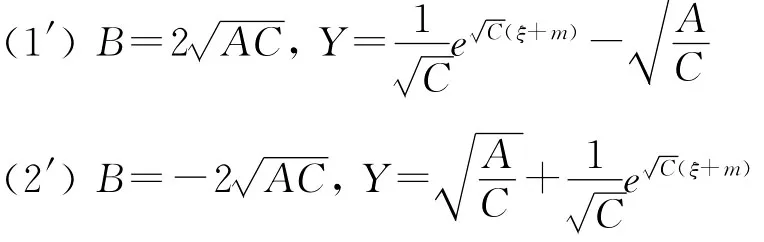
其中，m是积分常数。

情形（Ⅱ） r＝3，即Y′2＝A＋BY＋CY2＋DY3

其中，m是积分常数。

情形（Ⅲ）r＝4，即Y′2＝A＋BY＋CY2＋DY3＋EY4

其中，m是积分常数。

其中，m是积分常数。

3 应用举例

考虑Kdv方程

为了得到方程（6）的行波解，作如下变换

将方程（7）代入方程（6）并积分得

平衡方程（8）的最高阶倒数项u″和非线性项u2，得到n＝2，因此方程（8）的解可设为

将方程（9）代入方程（8）并使用方程（5），令Y各次幂系数为零，就得到a0，a1，a2，b1，b2，A，B，C，D，E，k，a，n，d，w的一个代数方程组

由前述主要结果，可知Kdv方程的解

情形 （Ⅰ）

（1）如果在方程（5）中取A＝C＝1，B＝D＝E＝0，则

其中，k是一个自由参数。

将这些结果代入方程（9），这时有Y＝sin hξ（m＝0），从而得到

（2）如果取A＝2，C＝－1，B＝D＝E＝0，则

（3）如果取A＝C＝1，B＝－2，D＝E＝0，那么

这时Y＝expξ＋1（m＝0），所以有

其中，u4与文献［1］中的单孤子解相同。

（4）如果取A＝C＝1，B＝2，D＝3＝0，则所得到的解与文献［3］相同。

情形 （Ⅱ）

（1）如果取C＝D＝4，A＝B＝E＝0，那么

这时Y＝－sec h2ξ，所以有

（2）如果取C＝－4，D＝4，A＝B＝E＝0，这时Y＝sec2ξ（m＝0），那么就有

特别地，如果取D＝－C（C＞0），k＝1，则方程（6）有如下形式的解

与文献［1］中相同。

情形 （Ⅲ）

（1）如果取A＝B＝D＝0，C＝1，E＝－1，那么

（2）如果取A＝B＝D＝0，C＝－1，E＝1，那么

（3）如果取B＝D＝0，A，C，E≠0，那么

分别令C＝－2，E＝1，A＝1和C＝2，E＝1，A＝1，则得到

此结果同文献［4］。

（5）如果取A＝B＝0，C＝1，E＝D＝4，那么

其中，ξ＝k（x＋k2t）＋ξ0

由此可知此新的方法的有效作用。

［1］Fan E G.Integrable Systems and Computer Algebra［M］.Beijing：Science Press，2004：29－33.

［2］Chen D Y.Introduction of Solitons［M］.Beijing：Science Press，2006：15－16.

［3］Wazzan L.A modified tanh-coth method for solving the Kdv and the Kdv－Burger's equations［J］.Commun Nonlinear Sci Numer Simul，2009，14（2）：443－450.

［4］Li Y S.Solitary Theory and Integrable System［M］.Shanghai：Shanghai Technology Education Press，1999：41－43.

［5］Ablowitz M J，Segur H.Solitons and Inverse Scattering Transform［M］.SLAM：Society for Industrial Mathematics，2000.

［6］Vakhnenko V，Parkes E J.A bacldund transformation equation［J］.Chaos Solitons Fract，2003，17（4）：683－692.

［7］Hirota R.Direct method of finding exact solutions of nonlinear evolution equations［C］／／Bullough R，Caudrey P.Backlund transformations.Berlin：Springer，1980：1157－1175.

［8］Wazwaz A M.Mutiple－soliton solutions for the KP equation by hirota's bilinear method and by the tanh－coth method［J］.Appl Math Comput，2007，190（1）：633－640.

［9］Wazwaz A M.Mutiple－soliton solutions for the boussines equation［J］.Appl Math Comput，2007，192（2）：479－486.

［10］Malfliet W.Solitary wave solutions of nonlinear wave equation［J］.AMJ Phys，1992，60（7）：650－654.

［11］Malfliet W，Hereman W.The tanh method I：exact solutions of nonlinear evolution and wave equations［J］.Phy Scr，1996，54（6）：563－568.

［12］Wazwaz A M.The tanh method for travelling wave solutions of nonlinear equations［J］.Appl Math Comput，2004，154（3）：713－723.

（责任编辑：肖恩忠）

Construction of Exact Travelling Wave Solutions and Applications

FENG Bin－lu
（Weifang University，Weifang 261061，China）

In this work，a uniform construction of exact travelling wave solution was obtained by taking advantage of the modified ricati equation.And model was presented to show a wide applicability for handling nonlinear wave equations.

construction，travelling wave solution，Kdv equation

2011－02－22

山东省自然科学基金资助项目（ZR2009AL021）

冯滨鲁（1963－），男，山东泰安人，潍坊学院数学与信息科学学院博士，教授，博士生导师。研究方向：微分方程稳定性理论，孤立子理论。

O175.29 文献标识码：A 文章编号：1671－4288（2011）06－0001－05