Hilbert空间中严格伪压缩映像有限族公共不动点的迭代算法

刘立红，周海云，陈东青

（军械工程学院基础部，河北石家庄 050003）

Hilbert空间中严格伪压缩映像有限族公共不动点的迭代算法

刘立红，周海云，陈东青

（军械工程学院基础部，河北石家庄 050003）

给出了Hilbert空间中严格伪压缩映像有限族公共不动点的一个新的具有显式表达的迭代算法，并利用所给出的算法证明了一个强收敛定理.

Hilbert空间；严格伪压缩映像；公共不动点；迭代算法

MSC 2010：34A05

1 预备知识

用H表示实Hilbert空间，内积和范数为〈·，·〉和‖·‖，F（T）＝｛x∈H｜Tx＝x｝表示映像T的不动点集.设C⊂H是非空闭凸子集，记P c∶H→C是H到C上的投影.用表示序列的“强收敛”和“弱收敛”.

定义1 称T∶C→H是非扩张映像，若对∀x，y∈C，满足

定义2［1］称T∶C→H是firmly非扩张映像，若对∀x，y∈C，满足

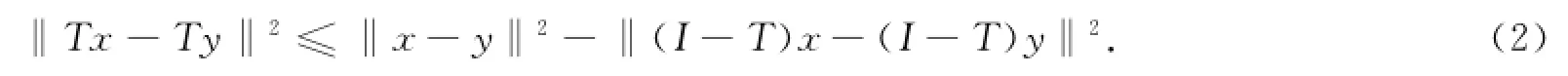
定义3［1］称T∶C→H是严格伪压缩映像，若存在常数0≤k＜1，对∀x，y∈C，满足

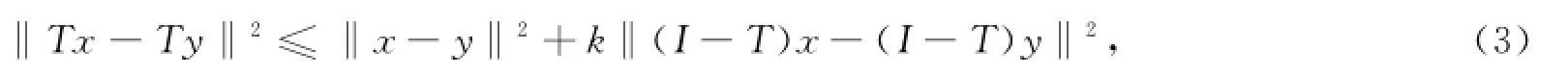
也称T是k-严格伪压缩映像.

注1 由定义可知，firmly非扩张映像一定是非扩张的，而非扩张映像是0严格伪压缩的.

2001年，Bauschke与Combettes［1］针对定义在Hilbert空间中的firmly非 扩张映像类建立了一种弱强收敛原理，并给出了算法的显式表达.2003年，Nakajo与Takahashi［2］针对定义在Hilbert空间中闭凸子集上的非扩张映像证明了一个强收敛定理，但没给出算法的显式表达.2007年，Marino与Xu［3］针对定义在Hilbert空间中闭凸子集上的严格伪压缩映像证明了强收敛结果，推广了Nakajo与Takahashi中的相关结果，但仍未给出算法的显式表达.针对定义在Hilbert空间中的闭凸子集上的严格伪压缩映像有限族提出一种新的杂交投影算法，并证明了算法的收敛性.此算法的最终投影具有显示表达.

为证明主要结果，引入下述引理：

引理1［4］设H是内积空间，对所有∀x，y∈H，α∈［0，1］，有

引理2［5］设C为Hilbert空间H中的非空闭凸子集，设x∈H，u0∈C，则

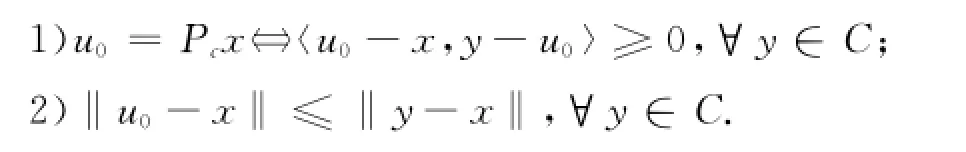
2 主要结果

显然Fα是H的非空闭凸子集，由引理2知，对∀x∈H，存在唯一的u0∈F a，使得u0＝P Fa（x0）.对于固定的正整数m，∀z∈H n＋m，有‖x n＋m－x0‖＝‖P Hn＋m x0－x0‖≤‖z－x0‖，所以｛x n｝有界，由式（6）知｛zn｝也有界.由u0∈Fa⊂H n＋m得，对∀n≥0，‖x n＋m－x0‖≤‖u0－x0‖.

由H n的定义，显然H n＋m⊆H n，即对∀n≥0，有‖x n－x0‖≤‖xn＋m－x0‖，所以｛‖xn－x0‖｝为单调有界序列.于是存在常数c，使得lim‖x n－x0‖＝c.由引理2知x n＋m∈H n，x n＝P H x0，且〈x n－x0，x n＋mx n〉≥0，因此

由于lim‖x n－x0‖＝c，所以｛x n｝为柯西列，即

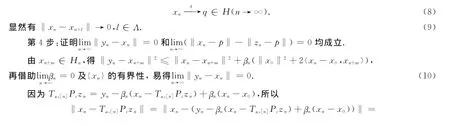
结合式（8）与式（14）可得q∈Fα.由迭代格式（4）与引理2，得q＝P Fα（x0）＝P F（x0），即序列｛x n｝强收敛于P F（x0）.同理，结合式（10），（11），序列｛yn｝和｛z n｝也强收敛于P F（x0）.即序列｛x n｝，｛y n｝和｛zn｝均强收敛于PF（x0）.

［1］BAUSCHKE H H，COMBETTES P L.A weak－to－strong convergence principle for Fejer－monotone methods in Hilbert spaces［J］.Mathematics of Operations Research，2001，26：248－264.

［2］NAKAJO K，TAKAHASHI W.Strong convergence theorems for nonexpansive mappings and nonexpansive semigroups［J］.J Math Anal Appl，2003，279：372－379.

［3］MARINO G，XU H K.Weak and strong convergence theorems for strict pseudo－contractions in Hilbert spaces［J］.J Math Anal Appl，2007，329：336－349.

［4］白占立，陈东青，高改良，等.Hilbert空间中关于Lipschitzian单调算子的变分不等式逼近解［J］.河北大学学报：自然科学版，2010，31，（4）：344－348.

［5］谈斌.几类非线性算子零点或不动点迭代算法研究［D］.石家庄：军械工程学院，2004.

An Iteration Algorithm for Common Fixed Points About Finite Family of Strict Pseudo－contractive Mappings in Hilbert Spaces

LIU Li－hong，ZHOU Hai－yun，CHEN Dong－qing
（Department of Basic Courses，Ordnance Engineering College，Shijiazhuang 050003，China）

The new iteration algorithm for common fixed points about finite family of strict pseudo－contractive mappings in Hilbert spaces is given，which has an explicit expression.Then a strong convergence theorem is proved by the modified algorithm.

Hilbert spaces；strict pseudo－contractive mapping；common fixed points；iteration algorithm

O 177.91

A

1000－1565（2011）03－0236－04

2010－10－27

国家自然科学基金资助项目（11071053）

刘立红（1972－），女，河北保定人，军械工程学院讲师，主要从事非线性泛函分析及其应用研究.E－mail：liulihong2003＠sohu.com

王兰英）