直觉模糊支持向量机

哈明虎，黄澍，王超，王晓丽

（1.河北大学数学与计算机学院，河北保定 071002；2.河北大学物理科学与技术学院，河北保定 071002）

研究报告

直觉模糊支持向量机

哈明虎1，黄澍1，王超2，王晓丽1

（1.河北大学数学与计算机学院，河北保定 071002；2.河北大学物理科学与技术学院，河北保定 071002）

传统的模糊支持向量机难以区分具有相同隶属度的稀疏样本点和稠密样本点，进而可能降低分类精度.为了解决此类问题，利用直觉模糊集和模糊支持向量机，构建了直觉模糊支持向量机.仿真实验结果表明：与传统的支持向量机和模糊支持向量机相比，直觉模糊支持向量机的分类结果更精确.

模糊支持向量机；直觉模糊集；直觉模糊支持向量机

MSC 2010：90－04

支持向量机（support vector machine，SVM）是Vapnik［1］基于统计学习理论提出的一种通用机器学习方法，目前已成为机器学习领域一个重要的研究方向［2］.一般的SVM在训练的时候对所有训练点同等对待，将每一训练点的全部信息加以学习，这就产生一定的局限性.例如：由于样本中的每一个训练点起的作用不同，支持向量起决定性作用，非支持向量基本不起作用，而噪音点或野点则对正确分类起负面作用，所以分类时应对训练点区别对待，尽可能保留支持向量，剔除非支持向量，消除噪音点及野点.针对这种情况，Lin等［3－4］构建了模糊支持向量机（fuzzy support vector machine，FSVM），根据不同输入样本对分类的贡献不同，赋以不同的隶属度，从而削弱了噪声或野点对分类的影响.如何确定训练样本的隶属度是FSVM方法的关键点，目前较为常用的方法是根据样本到聚类中心的距离来确定隶属度的大小［5］，但这种方法的局限性在于没有考虑样本之间的紧密程度.若给定稀疏、稠密2类样本点，则前者比后者更有可能成为野点.如果两者到聚类中心的距离相等，则两者都被赋予了相同的隶属度，从而易造成较大分类误差.模糊集是构建模糊支持向量机的基础，是Zadeh［6］于1965年提出的，已在现代社会的众多领域得到了广泛应用［7］.然而，模糊集中元素的隶属度仅是一个实数，它在决策等实际应用中，只能表示支持（肯定）、反对（否定）和犹豫（不确定）之一的程度，不能同时表示支持（肯定）、反对（否定）和犹豫（不确定）3者的程度.例如：在各种投票活动中，除了支持与反对2个方面，经常有弃权情况发生.故单独使用隶属度模糊集在一些实际问题应用中存在一定的局限，基于此，Atanassov［8］拓展了Zadeh的模糊集，提出了基于隶属度、非隶属度和犹豫度这3个方面信息的直觉模糊集，使直觉模糊集比传统模糊集能够更细腻地描述和刻画客观世界中模糊性的本质［9］.Deschrijver等［10］研究了不精确框架下的直觉模糊集，Tamalika等［11］把直觉模糊理论应用在了边缘分析中.Vahid等［12－14］把直觉模糊集应用到了模式识别中取得了很好的效果，徐泽水［15］在直觉模糊集理论及应用方面也取得了系统的成果.本文把直觉模糊集应用到支持向量机中，提出了一种新的支持向量机简称为直觉模糊支持向量机（intuitionistic fuzzy support vector machine，IFSVM）.通过样本在高维空间的分布确定样本的隶属度和犹豫度，将样本直觉模糊化，再利用支持向量机对直觉模糊化的样本进行分类.

1 预备知识

定义1［6］设X是一个非空集合，则称

为模糊集，其中μF是模糊集F的隶属函数，μF∶X→［0，1］，μF（x）为x属于F的隶属度，且μF（x）在［0，1］取值.

定义2［9］设χ是一个给定论域，则χ上的一个直觉模糊集定义为

其中，μA∶x→［0，1］和νA∶x→［0，1］分别称为A的隶属函数和非隶属函数，则μA（x）对于A上所有x∈χ，0≤μA（x）＋νA（x）≤1成立.对于χ中的每一个直觉模糊子集，称πA（x）＝1－μA（x）为－νA（x）x属于A的直觉指数，是x属于A的犹豫度或不确定度.

显然，模糊集是直觉模糊集的一个特例.

2 模糊支持向量机

在传统的支持向量机中，最优分类面往往由少量的位于类边缘支持向量决定，而含野点的样本常常也位于类边缘，所以SVM在训练过程中对于外围野点数据十分敏感.为了减小传统支持向量机中异常数据点对SVM训练模型的影响，Lin等［3］构建了模糊支持向量机，其原理就是有区别地对待每一个训练数据，根据其贡献不同分配不同的权重，即为每一个样本确定一个隶属度.给定的训练数据集为｛x i，y i，si｝，其中i＝1，2，…，l，相应的类标签为yi＝｛－1，1｝.于是FSVM的最优分类面的目标函数的最优解

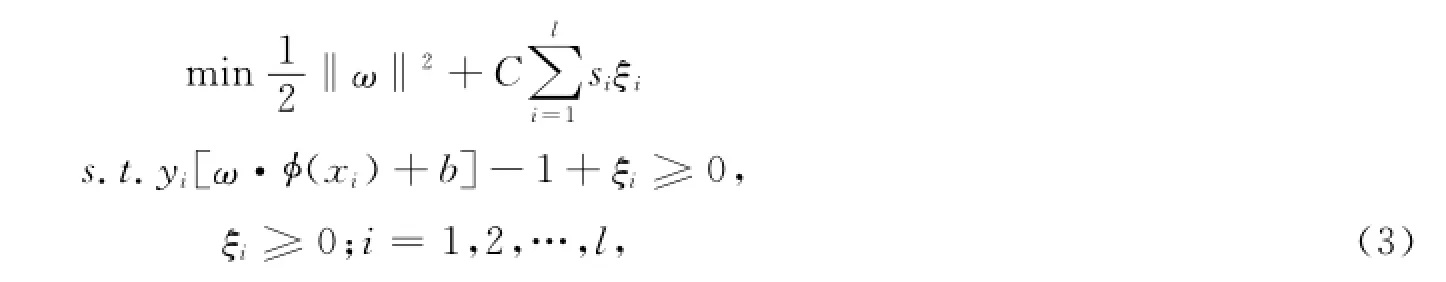
其中si为每个训练样本点的隶属度，在具体应用中采用不同方法生成.最后得到最优判别函数为

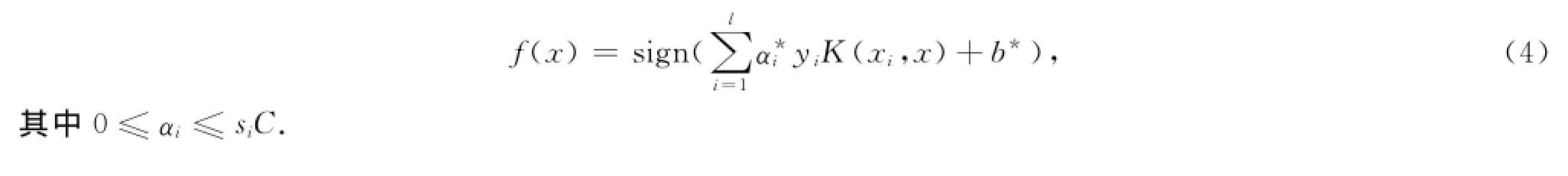
3 直觉模糊支持向量机

给定训练样本集T＝｛（x1，y1，μ1，π1），（x2，y2，μ2，π2），…，（x l，y l，μl，πl）｝，其中μi为样本x i的隶属度，πi为样本x i的直觉指数.

3.1 聚类中心的确定

3.2 原始数据的直觉模糊化

1）样本点之间的距离

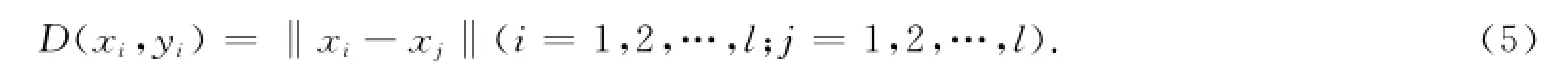
2）样本点的同类点密度、异类点密度分别为

式中｜｜表示集合的势，即集合中元素的个数，R为可调节的样本点邻域半径.

如图2，虚线内的样本为不存在异类样本的区域，错分率很低，赋予一个很大隶属度，虚线与实线间的样本为存在错分的样本赋予一个小的隶属度，同时赋予直觉指数.

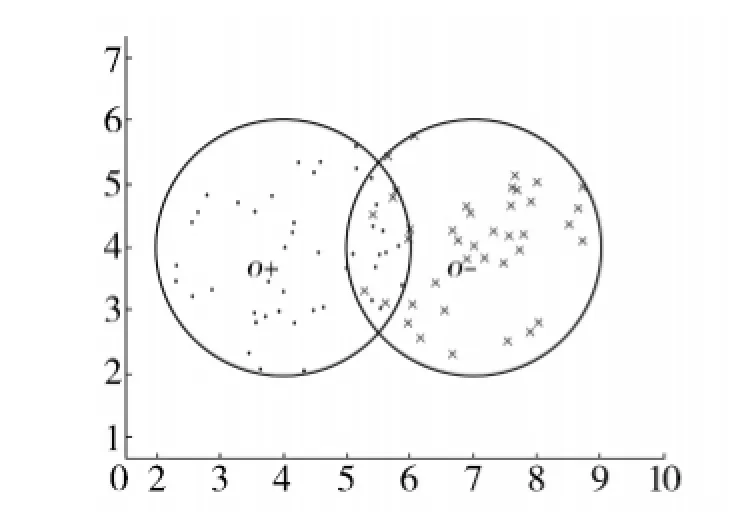
图1 数据的聚类中心Fig.1 Cluster center of data samples

图2 隶属度与犹豫度的表示 Fig.2 Expression of membership degree and hesitation degree

3）定义样本的隶属度

其中m为［0，1］的可调参数.

4）定义直觉指数

其中ρ＋＋为正类中同类密度，ρ＋－为正类中异类密度，ρ－＋为负类中同类密度，ρ－－为负类中异类密度，R为样本点的临域.

3.3 数据分类算法

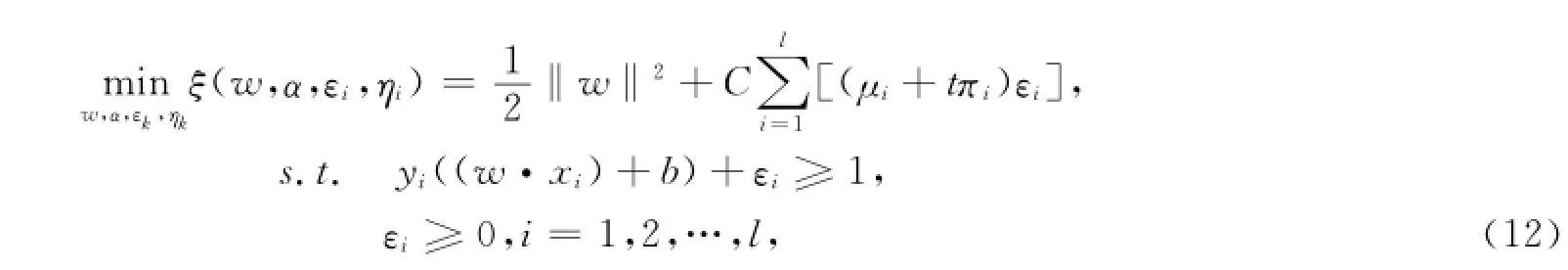
其中t为可调参数（t可以大于1，但要满足μi＋tπi≤1）.

引入Lagrange乘子

由此求解问题变为下面的二次优化问题

其中C＞0为惩罚参数，表示对错分样本惩罚的程度；μi为样本点的模糊隶属度；εi≥0为松弛变量；K（xi，y j）＝φ（x i）·φ（x j）为满足Mecer核定理的核函数.

4 仿真实验

采用MATLAB编程语言在PC机上对人工数据集进行实验.如图3所示，实验所用数据集为人工数据集，选取59个样本，取t＝2，R＝0.2，m＝0.5，正类用□表示，负类用×表示，核函数为多项式核函数d＝1，C＝5000，黑线为直觉模糊支持向量机，红线为模糊支持向量机，绿线为支持向量机.从图3可以看出，虽然有几个负类样本散落在正类中但由于样本点间的距离比较大，成为野点的可能性更大.而靠近负类的那3个正类样本比较紧密，成为野点的可能性较小，从图中可明显看出，SVM明显把那3个正类样本点归于负类，FSVM虽然较SVM有所修正但仍把那3个正类样本点归为负类，IFSVM则把边界那3个正类样本点归为正类，更符合人的判断的习惯

图3 人工数据集的分类结果Fig.3 Classification of artificial data sets

5 结论

为了较好地解决基于模糊集的模糊支持向量机存在的一类问题，基于直觉模糊集和模糊支持向量机，本文构建了直觉模糊支持向量机，它是模糊支持向量机的一种有意义的拓广.它通过样本点到聚类中心的距离确定样本点的隶属度，再通过单个样本附近样本点的紧密程度确定该样本的直觉指数，从而更准确地区分隶属度相同的不同样本点对该类的贡献程度，这样就使支持向量机对边缘样本点有所取舍，降低了野点的影响，提高了支持向量机分类的精度.仿真实验验证了该算法的有效性.把本算法应用到真实数据集及推广到多类问题是作者未来的研究方向.

［1］VAPNIK V N.The Nature of Statistical Learning Theory［M］.New York：Springer－Verlag，1995.

［2］哈明虎，王超，张植明，等.不确定统计学习理论［M］.北京：科学出版社，2010.

［3］LIN C F，WANG S D.Fuzzy support vector machines［J］.IEEE Transaction on Neural Networks，2002，13：464－471.

［4］LIN C F，WANG S D.Fuzzy support vector machines with automatic membership setting［J］.Studies in Fuzziness and Soft Computing，2005，177：233－254.

［5］张翔，肖小玲，徐光佑.模糊支持向量机中隶属度的确定与分析［J］.中国图象图形学报，2006，11（8）：1188－1192.

［6］ZADEH L A.Fuzzy sets［J］.Information and Control，1965，8：338－353.

［7］陈水利，李敬功，王向公.模糊集理论及其应用［M］.北京：科学出版社，2005.

［8］ATANASSOV K.Intuitionistic fuzzy sets［J］.Fuzzy Sets and Systems，1986，20：87－96.

［9］ATANASSOV K T.New operations defined over the intuitionistic fuzzy sets［J］.Fuzzy Sets and Systems，1994，61：137－142.

［10］DESCHRIJVER G，ETIENNE E.On the position of intuitionistic fuzzy set theory in the framework of theories modelling imprecision［J］.Information Sciences，2007，177：1860－1866.

［11］TAMALIKA C.A new measure using intuitionistic fuzzy set theory and its application to edge detection［J］.Applied Soft Computing，2008，8：919－927.

［12］VAHID K，GHOLAM A M.Intuitionistic fuzzy set vs.fuzzy set application in medical pattern recognition［J］.Artificial Intelligence in Medicine，2009，47：43－52.

［13］HUNG W L，YANG M S.On the J－divergence of intuitionistic fuzzy sets with its application to pattern recognition［J］.Information Sciences，2008，178：1641－1650.

［14］IOANNIS K V，GEORGE D S.Intuitionistic fuzzy information－Applications to pattern recognition［J］.Pattern Recognition Letters，2007，28：197－206.

［15］徐泽水.直觉模糊信息集成理论及应用［M］.北京：科学出版社，2008.

Intuitionistic Fuzzy Support Vector Machine

HA Ming－hu1，HUANG Shu1，WANG Chao2，WANG Xiao－li1
（1.College of Mathematics and Computer，Hebei University，Baoding 071002，China；2.College of Physics Science and Technology，Hebei University，Baoding 071002，China）

Since the traditional fuzzy support vector machine hardly distinguishes between sparse sample points and dense sample points with the same membership，it may further reduce the classification accuracy.In order to solve the problem，by using the fuzzy support vector machine and intuitionistic fuzzy sets，the intuitionistic fuzzy support vector machine is constructed.The simulation experiment shows that the classified result by using the intuitionistic fuzzy support vector machine is more accurate than the traditional fuzzy support vector machine and the fuzzy support vector machine.

fuzzy support vector machine；intuitionistic fuzzy set；intuitionistic fuzzy support vector machine

TP 181

A

1000－1565（2011）03－0225－05

2010－09－27

国家自然科学基金资助项目（60773062；61073121）；河北省自然科学基金资助项目（2008000633）；河北大学自然科学基金资助项目（2008－125）

哈明虎（1963－），男，河北肃宁人，河北大学教授，博士生导师，主要从事广义测度、不确定统计学习理论和智能管理方面的研究. E－mail：mhha＠hbu.edu.cn

王兰英）