基于主成分分析法的遗传神经网络模型对电力系统的短期负荷预测

黄媛玉，毛弋

（湖南大学信息科学与工程学院，中国长沙 410082;湖南大学电气工程与科学学院，中国长沙 410082）

基于主成分分析法的遗传神经网络模型对电力系统的短期负荷预测

黄媛玉，毛弋*

（湖南大学信息科学与工程学院，中国长沙 410082;湖南大学电气工程与科学学院，中国长沙 410082）

针对BP神经网络的两个主要缺点，网络训练速度慢，对初始权值阈值敏感，容易陷入局部极小点，本文利用多元统计分析的主成分分析方法（Principal components analysis，PCA），在不损失原始负荷数据主要信息的前提下提取负荷数据的主成分，有效地减少了预测模型的输入量.同时将遗传算法（GA）与BP神经网络结合，利用GA的全局搜索优化BP网络的结构参数，有效克服BP算法的局部收敛等问题.实验结果表明，该方法提高了预测精度，得到了较好的预测结果.

电力系统;负荷预测;主成分分析;遗传算法;BP神经网络

电力系统短期负荷预测是电力生产部门的重要工作之一，它主要用于预报未来几小时、一天至几天的电力负荷.通过准确的负荷预测，可以经济合理地安排机组启停，减少旋转备用容量，合理安排检修计划，降低发电成本，提高经济效益，是电力系统运行的安全性、经沪生和供电质量的重要保障.

BP神经网络已广泛应用于短期负荷预测中，其最主要的特点是有很强的非线性拟合能力，可映射任意复杂的非线性关系.具有高度的容错性和鲁棒性以及强大的白组织、自学习能力.

短期负荷预测中输入变量的选择直接影响神经网络的学习速度、网络结构的复杂性和网络泛化的精度.通常，为了提高负荷预测精度，输入变量必须包括尽可能多的影响因素，如当天的温度、湿度、风速、当天是否为工作日、休息日、节假日等，从而导致BP神经网络的输入节点数量过多，网络的复杂度增大，进而使得训练次数多，学习效率低，收敛速度慢.若初始权值阈值选取不当，又易形成局部极小而得不到全局最优.目前，为保证短期负荷预测预测精度，解决BP神经网络输入参数以及初始权值阈值的确定问题，国内外学者已做了大量的研究［1－5］.文献［4］提出了一种结合数据挖掘技术和神经网络的短期负荷预测模型，利刚数据挖掘中的聚类技术将历史负荷数据进行聚类，根据聚类后的分类信息对定性属性利用粗糙集进行属性约简，由约简结果进一步生成决策规则树，然后利用自适应神经网络进行预测.文献［5］提出了一种模糊神经网络模型，利用模糊理论处理非线性问题的能力以及从大量数据中抽取相似性的功能，赋予神经网络模糊的输入变量和模糊的权值阈值，通过训练不断调整神经网络权值阈值来适应环境变化，从而提高系统性能.

为解决这一系列问题，本文利用主成分分析方法对原始负荷数据进行适当的处理，去除数据间的相关性，删除其中的部分冗余信息，以降低数据的维数，得到主成分分量，然后再对这些主成分分量用GA－BP神经网络建模进行预测.由于采用了GA对BP神经网络的连接权进行优化，有效克服了BP算法的局部收敛等问题.通过算例结果分析，证明了该模型的有效性.

1 主成分分析方法

1.1 主成分分析的基本原理

主成分分析方法是一种将多个指标化为少数几个不相关的综合指标的多元统计分析方法.它是通过矩阵的特征分析来对原始数据进行线性空间投影，从而达到降低数据维数的目的，其优点在于它既保留了原数据的大部分信息，又去除了原始数据的相关性，减少了数据量，很好地实现了数据的降维和简化.利用主成分分析得到的主成分与原始变量之间的基本关系如下:（1）每个主成分都是各原始变量的线性组合;（2）主成分的数目大大少于原始变量的数目;（3）主成分保留了原始变量绝大多数信息;（4）各个主成分之间互不相关．

设对某一事物的研究涉及P个指标，分别用x1，x2，…，xP表示，这P个指标构成P维随机向量为X=（x1，x2，…，xP）′．对X进行线性变换，形成新的综合变量，用Y表示，即新的综合变量可以由原来的变量线性表示为下式:

式中满足ui′ui=1，Yi与Yj相互无关，Y1，Y2，…，YP的方差依次减小．则称Y1，Y2，…，YP为原始变量的第一、第二、…、第P个主成分．

1．2 主成分分析步骤

具体的计算步骤如下:（1）根据研究问题选取初始分析变量;（2）根据初始变量特性判断由协方差矩阵求主成分还是由相关矩阵求主成分;（3）求协方差矩阵或相关矩阵的特征根与相应标准特征向量;（4）得到主成分的表达式，计算各个主成分的方差贡献率及累计方差贡献率，从而选取主成分;（5）结合主成分对研究问题进行分析并深入研究．

2 遗传BP神经网络模型

2．1 BP神经网络的基本原理

BP神经网络是一种多层前馈神经网络，由输入层、隐含层和输出层组成，含有一个隐含层的神经网络结构如图1所示．

图1中，P代表输入层有P个分量的输入向量，n为样本数，X为输入矩阵，W1，W2，b1，b2，a1，a2，S1，S2，n1，n2分别为隐含层和输出层神经元的权重矩阵、阈值向量、输出向量、神经元数及加权和向量．

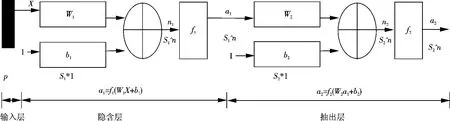
图13 层BP神经网络结构图

BP神经网络预测前首先要训练网络，通过训练使网络具有联想记忆和预测能力．BP神经网络训练过程包括以下几个步骤:

（1）网络初始化，把所有权值阈值都设置成较小的随机数．

（2）提供训练样本集，计算隐含层和输出层的输出．对于图1来说，隐含层的输出为a1=f1（W1X+b1）输出层的输出为a2=f2（W2a1+b2）．

（3）计算误差，调整权值阈值．

（4）反复进行步骤（2）～（3），直到误差满足精度为止．

2．2 遗传BP神经网络模型［6-7］

BP神经网络的学习就是对网络的权值和阈值进行学习和调整．为了避免因为初始权值阈值的选取不当，而造成网络在训练时陷入局部最小，本文引入遗传算法对网络初始参数进行优化．所谓网络参数的优化，就是寻找良好的网络权值和阈值．使得网络全局误差极小化．

具体的实现步骤如下:

（1）参数编码:将BP网络的权值和阈值作为基因，采用二进制编码方式进行编码，每个基因编码代表解空间的一个解．

（2）在编码的解空间中，随机生成一个初始群体（不要求一定是可行解）．

（3）对群体中的每一个个体进行适应度评价，本文采用BP神经网络训练得到的误差作为适应度函数．

（4）选择操作:按轮盘赌法将当前解群体中适应度最高的个体结构完整地复制到下一代群体中．

计算自适应交叉概率，对个体进行交叉．

（6）变异操作:将个体按照适应度大小进行排序，计算自适应变异概率，对个体进行变异操作．

（7）反复进行步骤（3）～（6），每进行一次循环称为群体进化了一代，直至进化了K代（K为预置的进化代数）．

（8）从第K代群体中选出适应度值最大的个体，该个体对应的就是BP神经网络训练时的权值和阈值的最佳初始解．

（9）利用训练好的神经网络进行预测．

3 主成分分析的遗传神经网络算法模型

将PCA、GA算法和BP神经网络三者结合，建立预测模型，利用PCA先对原始数据进行适当的处理，筛选出主成分，从而确定BP神经网络的拓扑结构，然后再利用GA算法从初始权值阈值的解群中选取出一组优秀的初始权值阈值.目的是为了克服传统神经网络的两大主要缺点:（1）输入变量过多时，网络结构复杂，训练速度慢，学习速度急剧下降;（2）初始权值阈值选取的盲目性，使得训练容易陷入局部极小点.对传统BP神经网络进行改进后，由于相对稳定了训练次数和最终权值阈值，大大加快了训练速度.

由于短期负荷预测中的输入变量中，常常涉及到负荷、温度、天气因素等不同的指标，同时本文BP网络每层神经元节点的激活函数采用sigmoid函数，必须:降输入量处理为区间［0，1］之间的数据，所以从相关系数矩阵出发进行主成分分析.具体步骤如下:

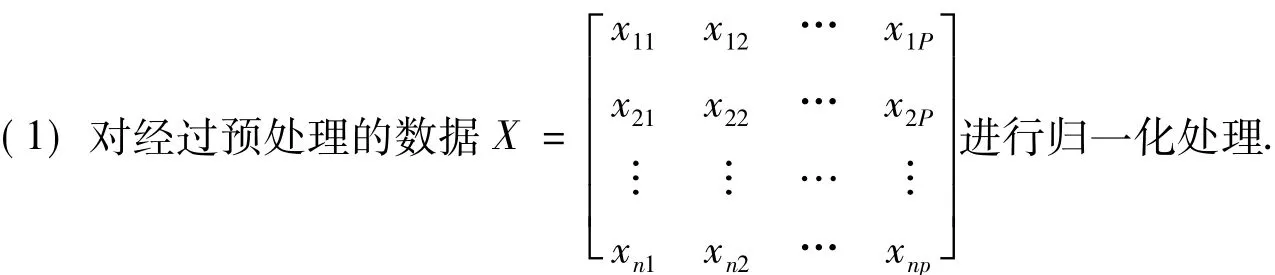
归一化方法有很多种形式，这里采用公式:

n为样本数，每个样本为P维;xij为第i个样本的第j维的取值;x1，x2，…，xp表示X的各列向量;xi．max，xi．min分别为第i个样本中的最大、最小值．在实际应用中，xi．max一般取实际最大值的1．1倍;xi．min一般取实际最小输入量得0．9倍．若为温度值，一般取xi．min=－50℃，xi．max=50℃．

（2）计算样本各维间相关系数矩阵R（rij）P×P．

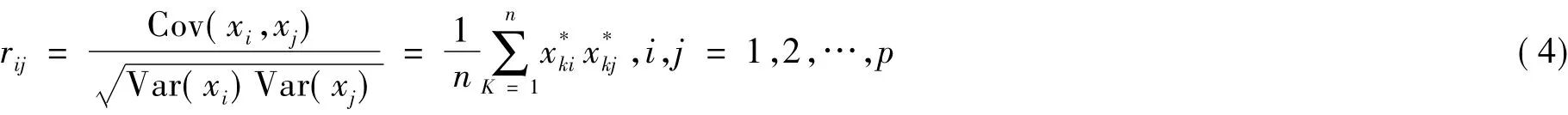
式中Cov（xi，xj）表示数据矩阵中第i列和第j列之间的协方差;Var（xi），Var（xj）为xi、xj的方差，计算公式为

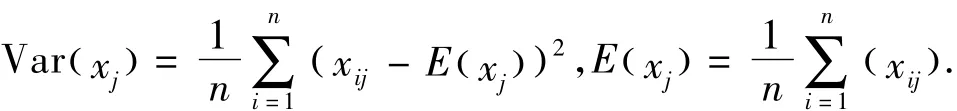
（3）求相关系数矩阵只的特征值和特征向量．

求得R的p个特征值λ1，λ2，…，λp（特征值均大于等于零）及相应的特征向量e1，e2，…，ep．

（4）求各个主成分的方差贡献率．

第k个主成分Yk的方差贡献率为

（5）筛选主成分．

将各主成分的方差贡献率由高到低排列，计算累计方差贡献率

当前m个主成分的累计方差贡献率达蓟桔息反映精凌的要求，即满足M≥85%时，求出λ1，λ2，…，λm对应的特征向量e1，e2，…，em，利用公式:

求得m个主成分（Y1，Y2，…，Ym）作为遗传BP神经网絡的输入变量．

显然，第k个主成分Yk=e'kX，k=1，2，…，m，将第i个样本的值（xi1，xi2，…，xip）代入Yk的表达式，经计算得到的值称为第i个样本在第k个主成分的得分，记为Yik=e'k（xi1，xi2，…，xip）．

主成分分析的遗传神经网络示意图如图2所示．

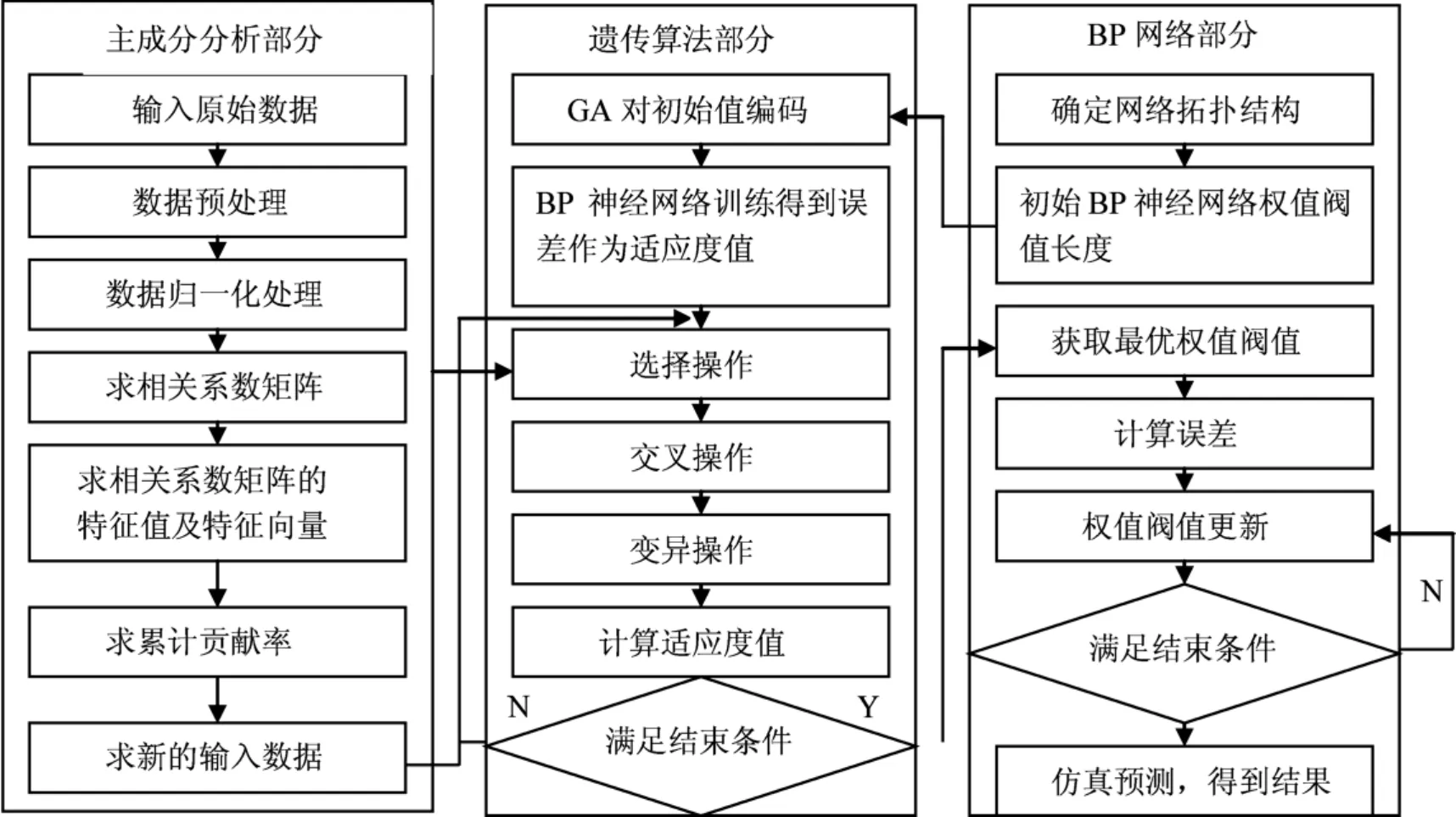
图2 主成分分析的遗传神经网络示意图

4 负荷预测仿真试验

为了验证所述主成分分析的遗传神经网络的可行性和有效性［8］，以南方某市的2004年7月10日到7月20日的12个整点有功负荷值以及2004年7月11日到7月21日的最高气温、最低气温和天气特征值（晴天、阴天还是雨天）为原始数据，对7月21日的日负荷进行预测建模为例进行讨论．日负荷预测的影响因素集见表1．

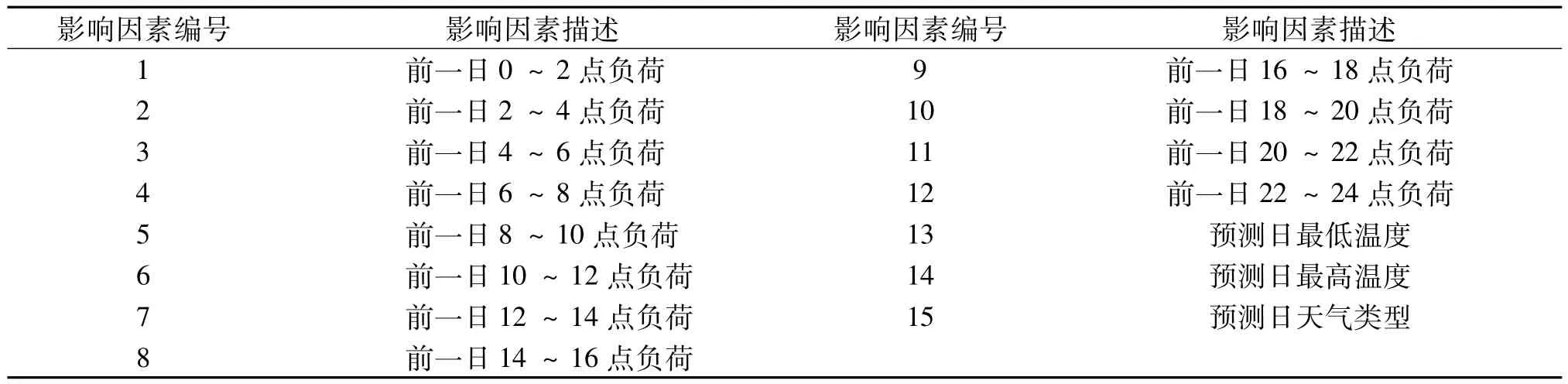
表1 日负荷预测的影响因素集

故有15个输入变量．本文将获得的原始数据预处理之后，利用公式（3）将其进行归一化处理，然后求出相关系数矩阵，利用公式（6）计算累计方差贡献率，见表2．

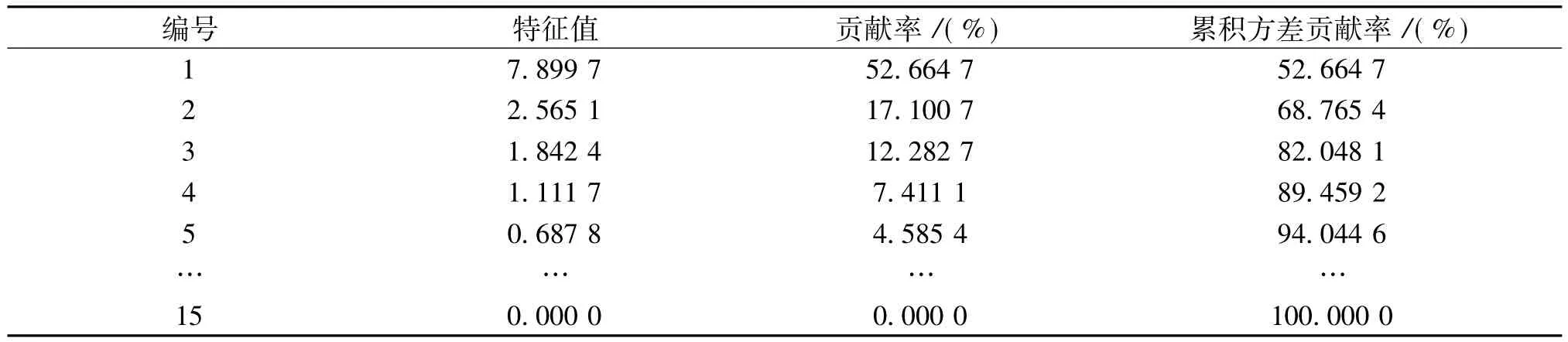
表2 特征值及累计方差贡献率

由表2可确定前4个特征值的累积方差贡献率已经大于85%，所以选择4个主成分．选定4个主成分后，利用公式（7）计算出新的输入变量．将得到的输入变量输入遗传神经网络中进行预测．

5 预测结果的比较

运用matlab编程并进行仿真训练，对未经过主成分分析的数据，建立BP神经网络模型和GABP遗传神经网络模型.输入层有工5个神经元，输出层有工2个神经元，隐含层节点的选取采用反复试验的方法，确定为31个.对经过主成分分析的数据，同样建立BP神经网络模型和GABP遗传神经网络模型.输入层有4个神经元，输出层有土2个神经元，反复试验后，确定隐含层节点为24个.神经网络隐含层节点转移函数选用tansig函数，输出层节点转移函数选用pure帆函数.表3是在4组不同的神经网络性能及预测误差比较.图3为4组不同的神经网络预测的相对误差曲线.

表34 组不同的神经网络性能及预测误差比较

从表3可以看出，主成分分析的遗传神经网络消除了网络输入因子间的相关性，减少了输入变量，简化了网络结构，提高了预测精度.从图3可以得出PCA－GABP网络预测各个点的相对误差较小，各点的可靠性大.

6 总结

利用PCA对样本集进行筛选，选出新的训练和测试样本集，从而减少了BP神经网络建模时的输入个数，同时消除了输入因子的相关性并简化网络结构，大大提高网络的学习速率.用GA的全局搜索能力来优化BP网络的结构参数，有效地克服BP算法易陷入局部收敛等问题，并将基于主成分分析的遗传神经网络的数学模型成功地应用于短期负荷预测研究中［9－11］.得到的PCA－GABP神经网络模型能达到较高的精度，为影响因素多且机理尚不清楚的电力市场提供了一个有效的方法和手段.

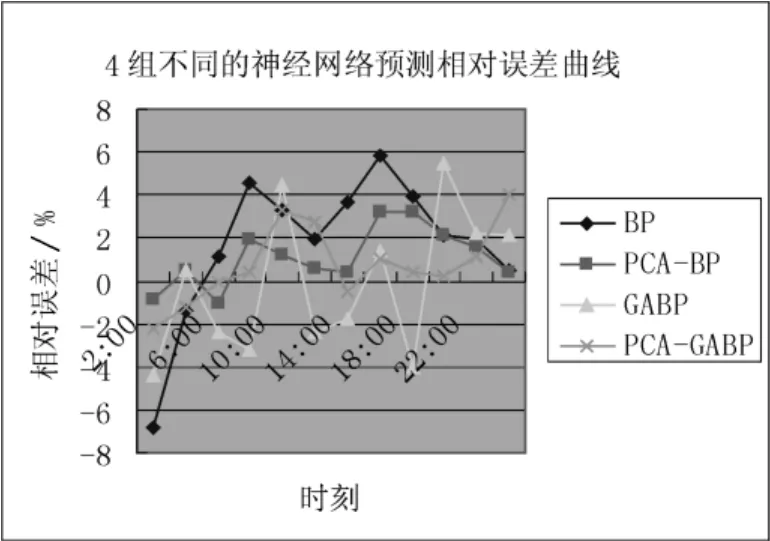
图34 组不同的神经网络预测相对误差曲线

［1］高山，单渊达.神经网络短期负荷预测输入变量选择新方法［J］.电力系统自动化，2001，25（20）:41－44.

［2］尹成群，康丽峰，孙伟，等.基于粗糙集和主成分分析结合的短期负荷预测［J］.华北电力大学学报，2007，34（1）:1－4.

［3］张晓星，周淙，任海军，等.基于增量约简算法确定电力负荷预测模型输入参数的研究［J］.电力系统自动化，2005，29（13）:40－44.

［4］牛东晓，王建军，李莉，等.基于粗糙集和决策树的自适应神经网络短期负荷预测方法［J］.电力自动化设备，2009，29（10）:30－34.

［5］胡越黎，计慧杰.短期电力负荷预测的模糊神经网络方法［J］.应用科学学报，2009，27（1）:79－83.

［6］谢宏，程浩忠，张国立，等.基于粗糙集理论建立短期电力负荷神经网络预测模型［J］.中国电机工程学报，2003，23 （11）:1－4.

［7］雷绍兰，孙才新，周湶，等.基于径向基神经网络和自适应神经模糊系统的电力短期负荷预测方法［J］.中国电机工程学报，2005，25（22）:78－82.

［8］程其云，王有元，陈伟根.基于改进主成分分析的短期负荷预测方法［J］.电网技术，2005，29（3）:64－67.

［9］杜鹃，改进的TSK型动态模糊神经网络在短期负荷预测的应用［J］.电网技术，2010，34（4）:69－75.

［10］梁海峰，涂光瑜，唐红卫.遗传神经网络在电力系统短期负荷预测中的应用［J］.2001，25（1）:49－53.

［11］高海龙，张国立.改进遗传神经网络及其在负荷预测中的应用［J］.华北电力大学学报，2009，36（5）:37－40.

Power System Short-term Loading Forecasting by Genetic Neutral Network Based on Principal Components Analysis

HUANG Yuan-yu，MAO Yi*
（School of Information and Science，Hunan University，Changsha 410082，China;
School of Electrical Engineering and Science，Hunan University，Changsha 410082，China）

The principal components analysis was used in order to solve two main weaknesses of BP neural network such as the speed of network′s training is slow，sensitive to the initial weight and threshold，and easy to fall into the partial minimal point.The main component of load data can be obtained without losing initial load data of the main information so that the input quantity of the prediction model can be decreased.At the same time，the local convergence and other problems of BP algorithm can be effectively overcome based on the combination of genetic algorithm（GA）with BP neural network，and using GA′s global searching function to optimize BP network′s structure parameters.This model is applied in the power system short－term load forecasting simulation process.The results show that it can improve the performance of network and the accuracy of predictions.

power system;load forecasting;principal components analysis;genetic algorithm;BP neural network

TM743

A

1000－2537（2011）05－0026－06

2011－05－01

湖南省自然科学基金资助项目（10JJ5055）

*通讯作者，E－mail:breeze_hs@yahoo.cn

（编辑陈笑梅）