一种地面目标跟踪算法的设计与实现*
2011-12-07邱晓波刘洪岩朱东旭侯永强
邱晓波,刘洪岩,朱东旭,侯永强
(1装甲兵工程学院,北京 100072;2北京理工大学自动化学院,北京 100081)
0 引言
在现代战争条件下,实时准确地掌握敌我双方地面军事运动目标的战场位置及机动状态对于陆战平台指挥与控制系统起到至关重要作用[1-2]。目标跟踪理论最初是从跟踪空中目标发展起来的,对地跟踪系统相对来说发展比较晚,而且与对空跟踪相比,对地面目标的跟踪有其自己的复杂性,主要表现在:目标的运动更加多样、密度更大、探测率低、杂波密度大等[3]。但是不论地面环境如何复杂,与跟踪空中目标一样,对地面目标的跟踪算法仍然主要解决两个方面问题,即:机动目标运动模型及跟踪滤波算法。
针对地面目标的探测率低且杂波密度大的情况,多传感器信息融合技术能够最大限度的利用来自各个传感器的原始量测数据并行多层次的处理,从而为陆战平台目标跟踪系统提供精确的目标状态信息以获得最佳的作战效果[4]。因此在滤波算法设计上,采用多传感器加权观测融合Kalman滤波算法[5]进行目标的状态估计。
变结构交互多模型(VSIMM)估计方法是一种已成功地应用于对地面目标的跟踪的估计方法[6]。目前,应用变结构交互多模型估计方法实施对地面目标的跟踪都主要以先验的道路信息为基础。这种方法在应用于复杂战场和不确定的环境,以及跟踪坦克、越野车辆等具有高通过性的地面运动目标时,跟踪效能有限。针对地面装甲目标在不同的工作阶段运动状态不同[7]的特点,设计了新的模型自适应方法对此类目标进行跟踪。
1 变结构多模型算法
固定结构多模型算法(FSIMM)在滤波过程中整个模型集的结构保持不变,而变结构交互多模型算法(VSIMM)则考虑在不同时刻选用不同模型集。算法基本思想是:先建立一个总模型集,在跟踪过程中根据目标的模式状态在总模型集中选择匹配的模型组成子集,在跟踪的过程中,可以选取一个子集来覆盖目标的机动量,且各子集可以按一定的规则相互传递。
1.1 模型集的自适应
VSIMM算法包括两个部分内容:模型集的自适应及模型集合序列条件估计。文中在模型集的自适应上,采用模型组切换模型组切换算法(MGS)[8-9]实现。这是一个比较容易实现的VSIMM算法。MGS算法使用硬切换的方式。在模型组硬切换中,切换是根据一系列确定的规则来完成的。因此,在任何时刻仅有一个模型组在运行,它相对于使用整个模型集合的固定结构多模型算法在计算量上有本质的减少。MGS算法的一个循环周期的计算流程如图1所示[8]。
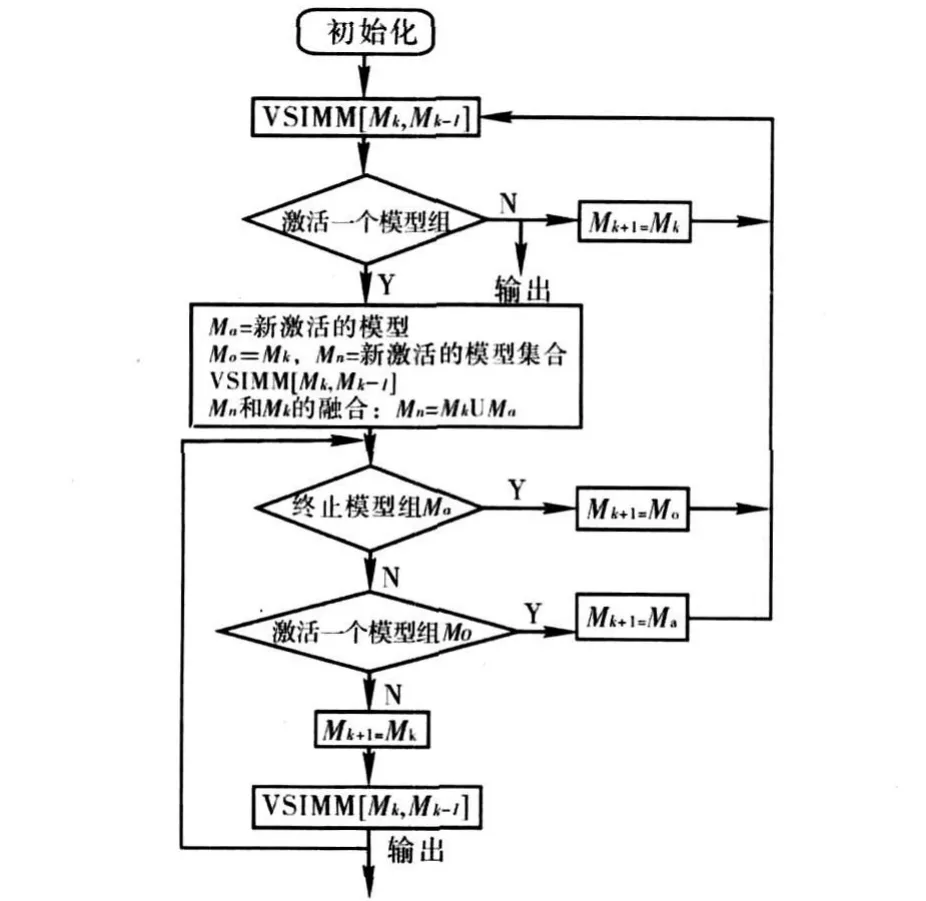
图1 MGS算法计算流程
1.2 模型集合序列条件估计
模型集合序列条件估计包括以下两步:
1)新模型和滤波器的初始化:即给新激活的模型分配初始概率以及为新激活的模型的滤波器确定初始状态估计和协方差。
2)算法的VSIMM[Mk,Mk-1]递归:新模型初始化的混合估计与IMM算法中的混合步骤是相同的。这个递归方法的特点是递归时自动对所有新激活的模型(滤波器)进行最优初始化:给所有的新激活的模型分配最优的初始概率,并基于这些模型的滤波器以最优的初始条件进行初始化。
模型集合序列条件估计具体计算过程可参考文献[8],此处不再赘述。
2 算法的具体设计
2.1 模型集设计
实际的战场环境下,坦克装甲车辆等军事目标由于具有强大的机动性能,在复杂多变的战场环境中仍具有较高的通过性,受到路网或其它地面环境的约束相对较小。所以,以地形或道路先验信息为基础的变结构交互多模型估计方法的跟踪算法将不再适用于跟踪该场景下的坦克等地面军事运动目标。对于坦克等越野车辆这类受道路情况影响不明显的目标,除公路网先验知识外,还可应用的先验信息包括:目标动力学模型、目标类型信息、目标所处环境地形信息、战术背景信息、目标电磁特征信息等[10]。为了简单起见,仅考虑应用以目标种类运动特性及运动模式先验信息[7],利用变结构交互多模型方法跟踪战场环境下的地面运动目标。
根据装甲目标特点,主要有以下几个工作阶段:起动阶段、行进阶段、射击阶段及规避运动阶段,处于不同阶段的坦克运动状态不同。在起动阶段,坦克驾驶员最有可能的操作为加速行驶;在行进阶段,坦克运动主要为匀速运动;在射击阶段,坦克驾驶员最有可能的操作为“减速—匀速—加速”行驶;坦克的规避运动主要为变加速运动或“S”形机动。由此可以确定4个模型组:
定义1:起动阶段模型组为m1,包含模型为匀速直线运动模型和匀加速直线运动模型;
定义2:行进阶段模型组为m2,包含模型为匀速直线运动模型;
定义3:射击阶段模型组为m3,包含模型为匀速直线运动模型和匀加速直线运动模型;
定义4:规避运动阶段模型组为m4,包含模型为匀速直线运动模型、匀加速直线运动模型和匀速率转弯运动模型[11]。
这样,4个模型组m1、m2、m3、m4分别对应坦克的起步阶段、迁徙阶段、射击阶段以及规避运动阶段。
2.2 加权观测融合Kalman滤波器
对多传感器系统,加权观测融合Kalman滤波原理是先将各传感器的观测方程在一定最优准则下融合为一个新的观测方程,然后将它们与状态方程联立可实现观测融合Kalman滤波器。
考虑各传感器的观测方程具有相同观测阵情形的加权观测融合Kalman滤波器。文献[5]已证明它具有全局最优性的优点。
Kalman滤波有两个基本方程:即状态方程和测量方程。对于一个目标跟踪系统而言,状态方程是描述目标运动的方程,假设目标运动模型用A表示,则目标跟踪系统的状态方程式为:
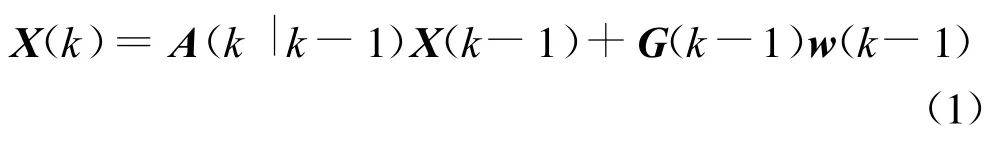
式中:X(k)为目标在tk时刻的n维状态矢量;A(k|k-1)为n×n维状态转移矩阵;G(k-1)为tk-1时刻扰动矩阵,w(k-1)为tk-1时刻均值为零、方差阵为Q的输入噪声。
L个传感器的跟踪系统观测方程为:

式中:Z i(k)为tk时刻第i传感器观测矢量,H(k)为观测矩阵,v i(k)为第i传感器观测噪声,其均值为零,方差阵为R i。
则多传感器观测方程组等价于一个加权观测融合方程:

其中:

相应的最优加权观测融合Kalman滤波器为:

其中,估值 Σ满足稳态 Riccati方程:

在实际应用中,为了减小计算负担,可设置一个死区T d,在一个周期T d内,估值Σ保持不变。仅在时刻t=T d,2T d,3T d…处计算估值 Σ,以减小计算负担。
3 算法仿真分析
为了验证此跟踪算法的跟踪性能,分别对固定结构交互多模型算法及上文算法在Matlab7.0上进行Monte Carlo仿真实验。其中IMM算法的模型集设定为一个CV模型,一个CA模型,一个匀速转弯(CT)[11]模型。变结构算法模型组为上文中的m1、m2、m3、m4。两种模型算法均采用加权观测融合Kalman滤波器进行滤波,设置死区T d=200,假设有3个相同传感器分别对目标进行观测,采样时间间隔T=1s,令系统噪声方差 σw=1,三个传感器测量噪声方差分别为=0.4,=2.5,σ2v3=6。假设被跟踪目标为一运动的坦克,Monte Carlo仿真次数设置为50次。不失一般性,仿真场景假设如下:
在二维空间内,首先模拟坦克的迁徙阶段,假设目标从原点开始运动,初始速度为(11,10)在 0~20s做匀速直线运动;20~70s模拟坦克战斗过程中规避运动即“S”形机动,假设目标作连续匀速率转弯机动,转弯速率 为 9°/s,70 ~90s模拟坦克射击阶段,假设目标首先作 6s的匀减速运动,加速度为(-1,-1.5),然后作10s的匀速运动,最后以加速度(2,1)作持续时间4s的匀加速运动。


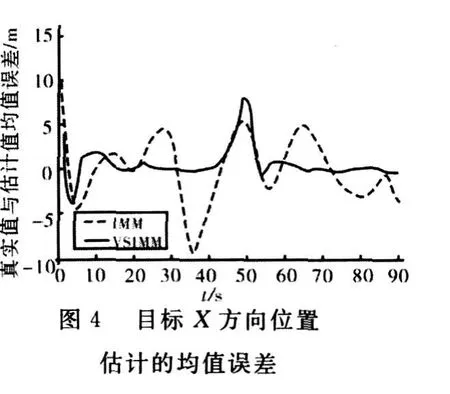


目标运动路径及基于两种算法的目标位置与速度估计如图2~图7所示。
仿真结果表明:在设置场景下,相对于固定结构的交互多模型算法,文中的算法具有比较理想的跟踪效果,位置及速度的均值及均方根误差都有一定的改善。虽然从精度上讲,该算法难以满足对目标进行射击的要求,但对于陆战平台指控系统,更加关注的是对于战场形势的把握、威胁评估,而该算法完全能满足要求。
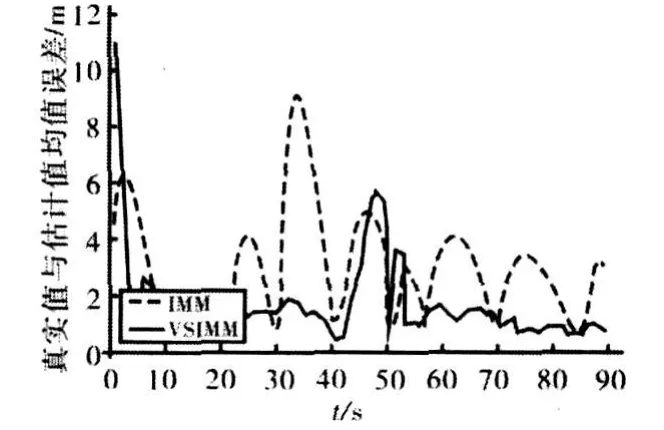
图7 目标X方向速度估计的均方根误差

表1 目标X方向位置及速度的平均误差
4 结论
文中针对地面运动目标的具体特点,具体研究了对一种地面运动目标(坦克)进行跟踪的VSIMM算法的应用,给出了算法的详细设计过程,仿真结果表明,采用本算法的目标跟踪精度比传统方案有所提高。为地面目标跟踪算法的设计提供了新的参考。
对于地面运动目标跟踪问题,变结构交互多模型算法有着巨大优势及应用前景,采用VSIMM算法,结合目标类型、运动特性以及道路、建筑、桥梁、地形、地貌可以被预先掌握的先验信息,将会对于地面目标跟踪的目标提供极大便利。
[1] 周启煌,候朝帧,陈正捷,等.陆战平台电子信息系统[M].北京:国防工业出版社,2006.
[2] 周启煌,常天庆,邱晓波.战车火控与指控系统[M].北京:国防工业出版社,2003.
[3] Chee-Yee Chong,David Garren,Timothy P Grayson.Ground target tracking,A historical perspective[C]//IEEE Transactions on Aerospace,Conference Proceedings,2000.
[4] 权太范.目标跟踪新理论与技术[M].北京:国防工业出版社,2009.
[5] 邓自立,王欣,高媛.建模与估计[M].北京:科学出版社,2007.
[6] T Kirubarajan,Bar-Shalom Y,L Kadar.Ground target tracking with variable structure IMM estimator[J].IEEE Transactions on Aerospace and Electronic Systems,2000,36(1):26-46.
[7] 黎阳诗,赵魏,毛士艺.基于变结构交互多模型的地面目标跟踪算法研究[C]//全国第十届信号与信息处理、四届DSP应用技术联合学术会议论文集:68-73.
[8] X R Li,X R Zhi,Y M Zhang.Multiple-model estimation with variable structure,Part III:Model-group switching algorithm[J].IEEE Transactions on Aerospaceand Electronic Systems,1999,35(1):225-241.
[9] X R Li,Y M Zhang,X R Zhi.Multiple-model estimation with variable structure,Part IV:Design and evaluation of model-group switching algorithm[J].IEEE Transactions on Aerospace and Electronic Systems,1999,35(1):242-254.
[10] 徐烨烽,李志宇,仇海涛,等.跟踪可移动地面目标的新途径[J].弹箭与制导学报,2008,28(3):71-73.
[11] 孙福明,吴秀清,王鹏伟.转弯机动目标的两层交互多模型跟踪算法[J].控制理论与应用,2008,25(2):233-236.
