缺失数据下多元正态模型Monte Carlo EM算法

王继霞，刘次华

(1.河南师范大学 数学与信息科学学院 河南 新乡 453007； 2.华中科技大学 数学与统计学院 湖北 武汉 430074)

缺失数据下多元正态模型MonteCarloEM算法

王继霞1，刘次华2

(1.河南师范大学 数学与信息科学学院 河南 新乡 453007； 2.华中科技大学 数学与统计学院 湖北 武汉 430074)

研究含有缺失数据的多元正态模型参数的极大似然估计问题，利用Monte Carlo EM算法求得多元正态模型参数的迭代解，并证明了此迭代解收敛到最优解，且其收敛速度是二阶的.

多元正态模型； 缺失数据； EM算法； Monte Carlo EM算法； Newton-Raphson算法

0 引言

EM算法[1-2]是常用的求后验众数的估计的一种数据增广算法，但由于求出其E步中积分的显式表达式有时很困难，甚至不可能，为了解决这个问题，将EM算法中的E步的积分用Monte Carlo模拟来有效实现，使其应用性大大增强.但是Dempster、Laird和Rubin[3-4]指出，EM算法的收敛速率是线性的，被缺失信息的倒数所控制，这样，当缺失数据的比例很高时，收敛速度非常缓慢.鉴于此，作者研究含缺失数据下多元正态模型参数的极大似然估计问题，将Monte Carlo EM算法与Newton-Raphson算法结合，给出均值向量的迭代解，并证明了该算法在后验众数附近具有二阶收敛速度.

1 参数的极大似然估计

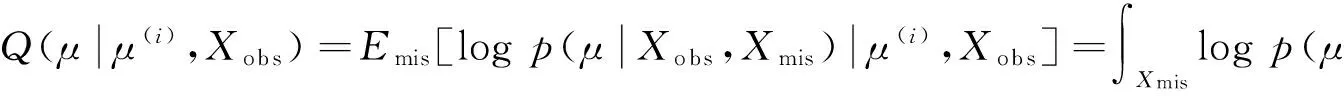
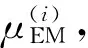
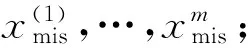
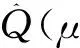
N-R步 令

(1)

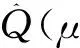
在上述算法中，由于μ的增广后验分布与缺失数据Xmis的条件预测分布易知且形式较简单，故N-R步中的数学期望与方差容易求得.

2 收敛性的证明

(2)

其中Gij(x)是Hesse矩阵G(x)的第i行第j列的元素，则对一切i，上述算法有定义，且当n充分大时，所得序列{μ(i)}收敛到最优解μ*，并且序列具有二阶收敛速度.

(3)

(4)

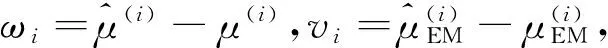
(5)

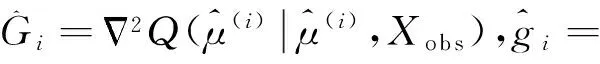
令h=-hi得

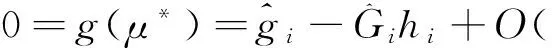
(6)

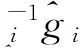
由O(·)的定义可知,存在常数C,使得

‖hi+1‖≤C‖hi‖2,

(7)

‖hi+1‖≤γ‖hi‖,

[1] Little R J A, Rubin D R. Statistical Analysis with Missing Data[M]. New York: Wiley,1987.

[2] Shi N Z,Zhong S R,Guo J H.The restricted EM algorithm under inequality restrictions on the parameters[J].Journal of Multivariate Analysis, 2005,92(4):53-76.

[3] Booth J G, Hobert J P.Maximizing generalized linear mixed model likelihoods with automated Monte Carlo EM algorithm[J].Journal of the Royal Statistical Society: Ser B, 1999,61(2):265-285.

[4] Dempster A P, Laird N M, Rubin D B. Maximum likelihood from incomplete data via the EM algorithm (with discussion)[J].Journal of the Royal Statistical Society: Ser B, 1977, 39(3):1-38.

[5] 罗季.Monte Carlo EM加速算法[J].应用概率统计,2008,24(3):312-318.

[6] Geweke J.Bayesian inference in econometric models using Monte Carlo integration[J].Econometrica,1989,57(2):1317-1339.

[7] 茆诗松,王静龙,濮晓龙.高等数理统计[M].北京:高等教育出版社,1998.

MonteCarloEMAlgorithmforMultivariateNormalDistributionunderMissingData

WANG Ji-xia1，LIU Ci-hua2

(1.CollegeofMathematicsandInformationScience,HenanNormalUniversity,Xinxiang453007,China; 2.DepartmentofMath,HuazhongUniversityofScienceandTechnology,Wuhan430074,China)

Maximum likelihood estimations of the parameters of multivariate normal distribution models under missing data were studied. The iterative solution of the parameters of multivariate normal distribution models were obtained through the Monte Carlo EM algorithm and this solution converge to the optimum solution were proved and the convergence rate of this solution was secondary.

multivariate normal distribution; missing data; EM algorithm; Monte Carlo EM algorithm; Newton-Raphson algorithm

O 212.1

A

1671-6841(2011)03-0059-03

2010-04-24

国家自然科学基金资助项目，编号10671057；河南省教育厅软科学研究计划,编号2010B110013.

王继霞(1978-),女,讲师,硕士，主要从事保序回归、约束统计推断等方面的研究，E-mail: jixiawang@163.com.