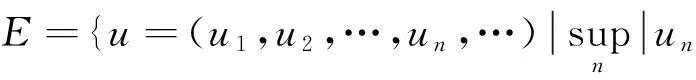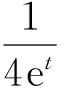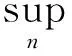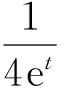Banach空间脉冲微分方程整体解的存在性
2011-12-02汪子莲
汪子莲, 丁 珂
(1.兰州工业高等专科学校 基础学科部 甘肃 兰州 730050; 2.中山大学 岭南学院 广东 广州 510275)
Banach空间脉冲微分方程整体解的存在性
汪子莲1, 丁 珂2
(1.兰州工业高等专科学校 基础学科部 甘肃 兰州 730050; 2.中山大学 岭南学院 广东 广州 510275)
利用Darbo不动点定理研究了Banach空间中一类含有无穷多个跳跃点的一阶脉冲微分方程初值问题,在较弱的条件下获得了其整体解的存在性.
正规锥; 脉冲微分方程; 非紧性测度; 初值问题
0 引言
脉冲微分方程理论研究在固定时刻或不固定时刻发生快速变化或跳跃的发展过程,是对自然界发展过程更直接的反映,近年来得到了广泛关注[1-4].
本文研究有序Banach空间E中脉冲微分方程初值问题
(1)

最近,抽象空间中脉冲微分方程初值问题得到了广泛的研究[2-4],但都是考虑在有限闭区间上局部解的存在性,并且考虑的是有限个脉冲点的情形.文[5-6]在耗散型条件下获得了没有脉冲的微分方程初值问题
(2)
在Hibert空间H中整体解的存在性.本文运用不同于文[5-6]的方法,获得了Banach空间E中含有无穷多个脉冲点的微分方程初值问题(1)整体解的存在性.
1 预备工作及引理
设E为有序Bananch空间,其正元锥P正规,正规常数为N,E中的序关系“≤”由锥P引出[7],x≤y⟺y-x∈P.


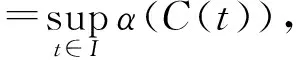

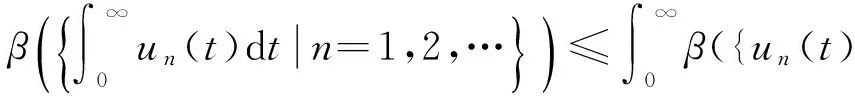
引理3(Darbo) 设E为Banach空间,Ω⊂E为非空有界凸闭集,若映像A:Ω→Ω是严格集压缩的,则A在Ω中必有不动点.
首先考察线性脉冲微分方程初值问题
(3)
其中h(t)∈BPC(J,E).
引理4对∀h(t)∈BPC(J,E),x0∈E和yk∈E,k=1,2,…,线性脉冲初值问题(3)有唯一解u∈BPC(J,E)∩C1(J′,E),且
(4)
证明设y0=θ,如果u∈BPC(J,E)∩C1(J′,E)是线性脉冲初值问题(1)的解,则u限制在Jk上满足线性微分方程初值问题
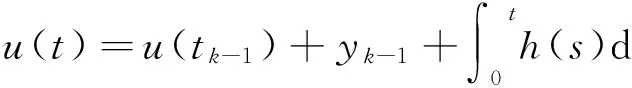
相反,直接验证可知,由(4)式定义的函数u(t)是直线性脉冲微分方程初值问题(3)的解.

引理5假设条件
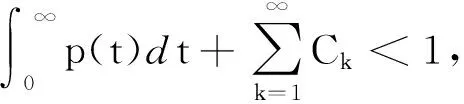
‖f(t,u)‖≤p(t)‖u‖+q(t),∀t∈J,u∈E;‖Ik(u)‖≤Ck‖u‖,k=1,2,…
成立,则A:BPC(J,E)→BPC(J,E)且u∈BPC(J,E)∩C1(J′,E)是问题(1)的解当且仅当u∈BPC(J,E)是算子A的不动点.
证明对∀u∈BPC(J,E),显然,Au∈BPC(J,E),于是

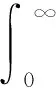
故‖Au‖≤R,从而Au∈BPC(J,E).因此,算子A有定义.又由引理4可知,u∈BPC(J,E)∩C1(J′,E)是问题(1)的解当且仅当u∈BPC(J,E)是算子A的不动点.


首先证明α(AC)≤d.事实上,由算子A的定义及假设H1易知(AC)(t)为Jk上等度连续的函数族,且对∀ε>0,∃N,当t1,t2>N时,对一切u∈C,有
‖(Au)(t1)-(Au)(t2)‖<ε.
(5)
因为函数族(AC)(t)在每个Ji(i=1,2,…,k)上等度连续,由引理1可知

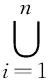
(6)
因而对∀Au1,Au2∈ACi,当t>tk时,由(5)式与(6)式,有
‖(Au1)(t)-(Au2)(t)‖≤‖(Au1)(t)-(Au1)(tk)‖+‖(Au1)(tk)-(Au2)(tk)‖+
‖(Au2)(tk)-(Au2)(t)‖<3ε+d,t>tk.
(7)
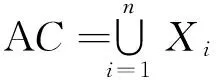
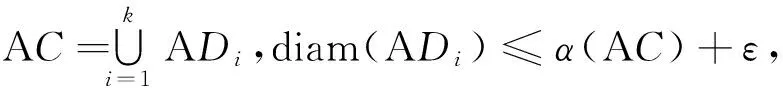
‖(Au1)(t)-(Au2)(t)‖≤‖Au1-Au2‖≤α(AC)+ε,
(8)


2 主要结果
定理1设E为有序Banach空间,其正元锥P正规,正规常数为N.f∈C(J×E,E),Ik∈C(E,E),k=1,2,….若条件H1满足,并且假设H2如下:
H2存在l∈L[0,+∞)及非负常数Mk,使得对任意有界集D⊂E,有
α(f(t,D))≤l(t)α(D);α(Ik(D))≤Mkα(D),k=1,2,…,
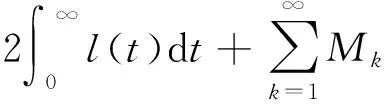
证明由算子A的定义、假设H1及引理5,易知A:BPC(J,E)→BPC(J,E)连续.
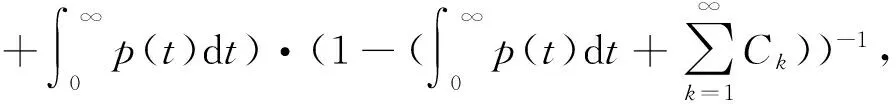
下面证明A:B→B.事实上,对∀u∈B,由算子A的定义及假设H1,有
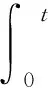

因此,A为从凸闭集B到B的连续算子.
由引理2及假设H2,有

由t的任意性可知

(9)
由(9)式、假设H2及引理2,有

(10)
所以,A:B→B为严格集压缩映射.
因此,由引理3可知,A在B中至少有一个不动点u,故u∈BPC(J,E)为问题(1)的解.证毕.
下面给出一个例子说明我们的结论.
例1考虑无穷维脉冲系统
(11)
其中,0 定理2脉冲微分系统(11)在[0,+∞)中至少存在一个解. (12) 显然,x0∈E,f∈C(J×E,E),Ik∈C(E,E),k=1,2,….下面验证H1与H2成立. 故H1满足. 由文[8-9]知,h(t,D)在E中相对紧,即α(h(t,D))=0,t∈J.因此,有 α(f(t,D))≤l(t)α(D),α(Ik(D))≤Mkα(D),t∈J,k=1,2,…, 故H2满足.因此,由定理1可知结论成立. [1] Lakshmikantham V,Bainov D D,Simeonov P S.Theory of Impulsive Differential Equations[M].Singapore:World Scientific,1989:2-18. [2] Sun Jingxian. Extremal solutions initial value problem for integro-differential of mixed type in Banach spaces[J].Ann Diff Eqs,1992,8(1):469-475. [3] Guo Dajun, Liu Xinzhi. Extremal solutions of nonlinear impulsive integro-differential equations in Banach spaces[J].J Anal Math Anal,1993,177(2):538-553. [4] Liu Xinzhi, Guo Dajun. Initial value problems for first-order impulsive integro-differential equations on unbound domains in a Banach space[J].Comm Appl Nonlinear Anal,1995,2(1):65-83. [5] Martin J R H. Differential equations on closed subsets of a Banach space[J].Trans Amer Math Aoc,1973,17(1):399-414. [6] Deiling K.On existence and uniqueness for differential equations[J].Ann Mat Pura Appl,1975,106(1):1-12. [7] 郭大钧.非线性分析中的半序方法[M].济南:山东科学技术出版社,2000:15-20. [8] Guo Dajun,Lakshmikantham V.Nonlinear in Abstract Cones[M].San Diego:Academic Press,Inc,1988:24-25. [9] 杨洁,孟风娟.一类二阶超二次哈密顿系统的周期解[J].郑州大学学报:理学版,2009,41(4):6-10. ExistenceofGlobalSolutionsforImpulsiveDifferentialEquationsinBanachSpaces WANG Zi-lian1, DING Ke2 (1.CollegeofBasicCourses,LanzhouPolytechnicCollege,Lanzhou730050,China; 2.LingnanCollege,SunYat-setUniversity,Guangzhou510275,China) By using Darbo fixed point theorem, a kind of initial value problems for first order impulsive differential equations with infinite skip points in a Banach space was studied.And the existence of global solutions was obtained under weak conditions. normal cone; impulsive differential equation; measure of noncompactness; initial value problems O 175.15 A 1671-6841(2011)03-0022-05 2010-05-08 甘肃省教育厅科研项目,编号0712B- 02. 汪子莲(1964-),女,副教授,主要从事常微分方程边值问题研究,E-mail:sapingddk@163.com.