有关纯子模结构研究

张金羽

（河南工业大学 理学院，河南 郑州 450001）

有关纯子模结构研究

张金羽

（河南工业大学 理学院，河南 郑州 450001）

讨论了模M的τ-挠根Tτ(M)的结构。利用Tτ(M)作为模M的τ-纯子模的最小性得出结论：Tτ(M)为M的所有τ-纯子模的交。

模；纯子模；τ-挠根Tτ(M)

0 引言

定义1[1]设R-mod是左R-模范畴，τ是R-mod中的一个挠理论，M是左R-模。M是τ-挠模当且仅当对任意的内射模E∈τ，有

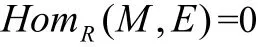
当且仅当存在一个内射模E′∈τ，使

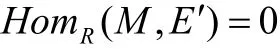
定义2[2]设R-mod是左R-模范畴，τ是R-mod中的一个挠理论，M是左R-模。M是τ-挠自由模当且仅当存在内射模E′∈τ及集合Ω，使

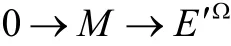
是正合列；当且仅当存在内射模E∈τ，使

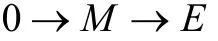
是正合列。

显然，τ-挠模与τ-挠自由模是两个对偶的概念。M既是τ-挠模又是τ-挠自由模当且仅当M=0。

1 Tτ( M)的结构描述

命题1 设τ是R-mod中的一个挠理论。M是左R-模，N是M的子模，则以下命题等价：

（i）M/N是τ-挠自由模；

（ii）存在

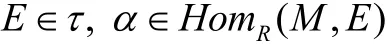
使

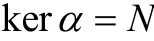
证明 （i）⇒（ii）由已知有内射模 ∈τ E ，使左R-模正合列

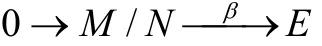
成立，因此存在模同态

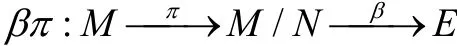
其中π是自然同态。

任取

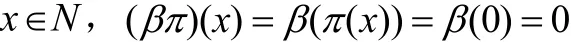
即

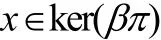
从而

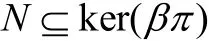
反之，任取

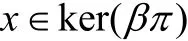
有

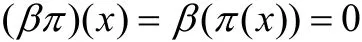
但β为单射，得

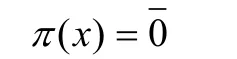
即x∈N，从而

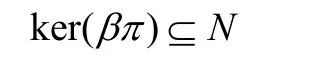
所以（ii）成立；

（ii）⇒（i）考察交换图。由于

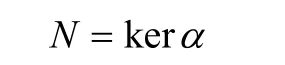
根据模同态基本定理，

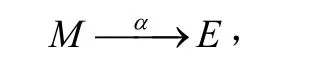
存在唯一的模同态π↓β

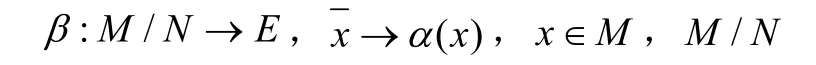
使图表可交换，即α=βπ，此时β为单的模同态，所以M/ N 是τ-挠自由模。

2 利用τ-纯度刻画τ-纯子模

定义3 设N是左R-模M的子模，称M的所有包含N的τ-纯子模的交为N在M中的τ-纯度，记作PurM(N)。

定理1 设τ是R-mod中的挠理论，N是左R-模M的子模，则以下命题等价：

（i）M/N是τ-挠模；

（ii）对任何

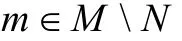
R /(N：m)是τ-挠模；

（iii）存在R的τ-稠密左理想I使Im⊆N。

证明 （i）⇔（ii）设M/N是τ-挠模，对任意的

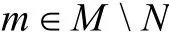
R (m + N)是M/N的非零子模。由于τ-挠模关于子模封闭，所以 R (m + N)是τ-挠模，又知有模同构

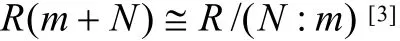
得结论成立；

反之，设 R /(N：m)是τ-挠模，那么由（*）式及m的取法知 R (m + N)是M/N的任意非零的循环子模，并且是τ-挠模。作直和

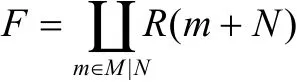
则易见M/N是F的商模。由于τ-挠模关于直和、商模封闭，所以M/N是τ-挠模；

（ii）⇔（iii）如果对任何

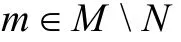
R /(N：m)是τ-挠模，那么(N：m)是R的τ-稠密左理想，又知

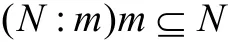
所以(N：m)为所求；

反之，如果有R的τ-稠密左理想I使得

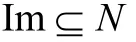
则

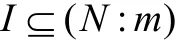
所以(N：m)是R的τ-稠密左理想，得 R /(N：m)是τ-挠模。

3 结论

给出了模M的τ-挠根Tτ(M)的一种新的结构描述，即Tτ(M)为M的所有τ-纯子模的交。

[1] J. S. Golan. Torsion Theories[M]. New York： John Wiley & Sons. Inc, 1986.

[2] J. Rotman. An Introduction to Homological Algebra[M]. New York： Academic Press, 1979.

[3] 周伯壎.同调代数[M].北京：科学出版社,1988.

（责任编辑、校对：赵光峰）

Research on the Structure of Pure Submodule

ZHANG Jin-yu

(School of science, Henan university of Technology, Zhengzhou 450001, China)

This paper discusses the problem of the structure of τ-torsion radical Tτ(M). Depending on the theory that τ-torsion radical Tτ(M) of M which is the minimum τ-pure submodule, it draw the conclusion： Tτ(M)is the intersection of all the τ-pure submodules of M.

module; pure submodule; τ-torsion radical Tτ(M)

2011-02-26

张金羽（1970-），男，吉林四平人，硕士，河南工业大学理学院讲师，研究方向为基础数学。

O154.2

A

1009-9115(2011)05-0007-02