关于一类特殊的射影平坦的(α, β)度量的构造

许 飞，张改平，张 欢

（装甲兵工程学院 基础部，北京 100072）

关于一类特殊的射影平坦的(α, β)度量的构造

许 飞，张改平，张 欢

（装甲兵工程学院 基础部，北京 100072）

构造了含五个参数的 F =α+β形式的(α,β) 度量，给出其射影平坦的条件，并计算了此种条件下的旗曲率。

(α, β)度量；射影平坦度量；Finsler度量；旗曲率

射影平坦是Finsler几何研究中非常重要的一个方面[1]，最早是由一个世纪前Hibert公布的第四问题转化而来，即找出所有的Finsler度量，使得直线具有最短路径，具有这种性质的Finsler度量称为射影平坦的Finsler度量。常旗曲率[2,3]也是Finsler几何中研究的一个重要方面，它是Riemann几何中截面曲率的推广，本文在此理论基础上构造了一类射影平坦且具有常旗曲率的例子。

1 Finsler几何

定义1 光滑流形M上的Finsler度量就是TM上的一个函数 F：TM → [0,+∞)，满足：

（1）正则性

F在TM{0}上光滑；

（2）一阶正齐次性

F (x,λy )=λF (x,y)，∀λ＞0；

则称F是流形M上的Finsler度量，赋予Finsler度量F的光滑流形M称为Finsler流形。

Rn中一个开集U上的Finsler度量F如果在U上的测地线全是直线，即测地线全σ(t)是常向量，则称度量F是射影平坦的，文献[4]给出了射影平坦的几个等价条件。

设F是Rn的开集U上的Finsler度量，则下面的几个条件是等价的：

（1）F在U上的测地线全是直线；

（2）F测地系数具有以下形式：

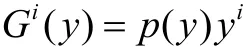
其中

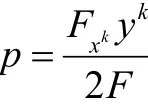
（3）F满足

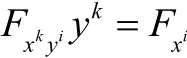
定义2 设(M,F)为Finsler流形，任给流形上一点x，设该点处的切空间中的旗平面P是由 {y,u} ⊂TxM 张成，旗曲率K(P,y)定义为

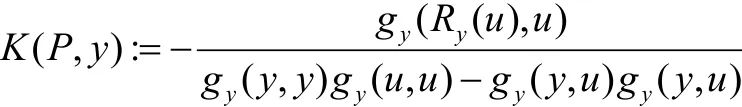
若K为常数，则称为常旗曲率。

Finsler度量中特殊而重要的一类度量是(α, )β度量，它是由一个Riemannn度量α，一个1-形式β以及光滑流形M上函数φ组成，具体形式是 F=αφ(β/α)，例如

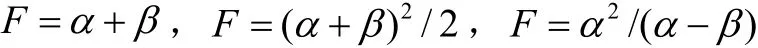
等都是(α,)β度量。

沈忠民[3]构造了一类局部射影平坦，具有零旗曲率的(α, )β度量，形式如下：

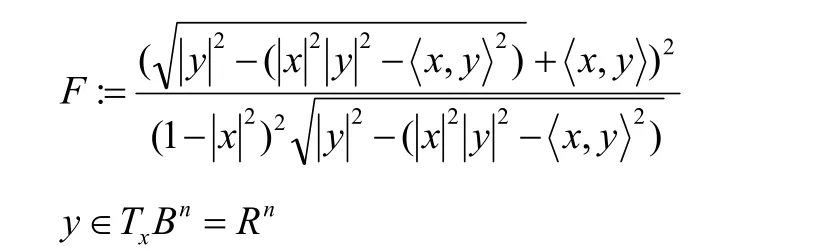
可以具体地将其看作为具有 F=(α+ β)2/α形式的(α, β)度量，其中

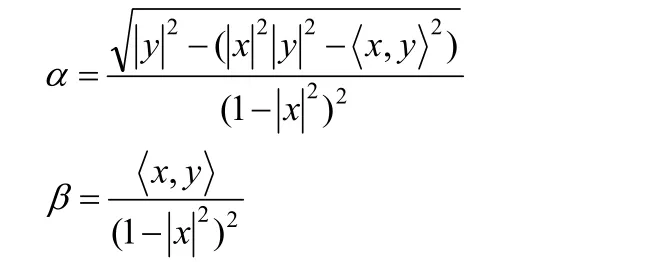
随后，杨春红[5]构造了一个具有三个参数的射影平坦，具有零旗曲率的(α, )β度量，形式如下：

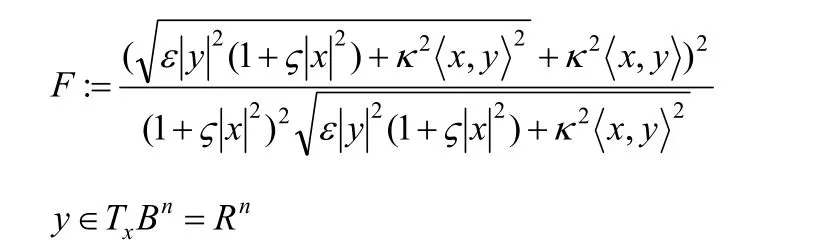
也可以具体地将其看作为具有 F=(α+ β)2/α形式的(α,β)度量，其中

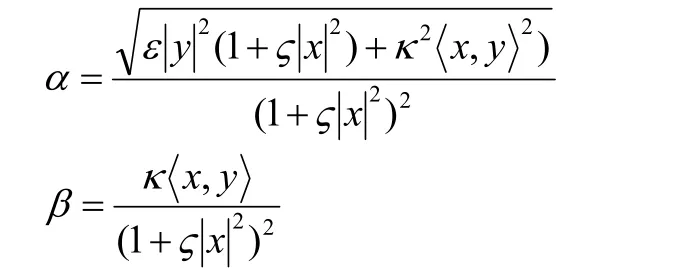
可见，文献[5]的构造是文献[3]的构造的推广。

本文将在此基础上对(α, β) 度量中的另外一种形式F =α+β，也即通常所讲的Randers构造了一个具有五个参数的Finsler度量，并讨论其射影平坦的条件和旗曲率。

2 射影平坦的条件

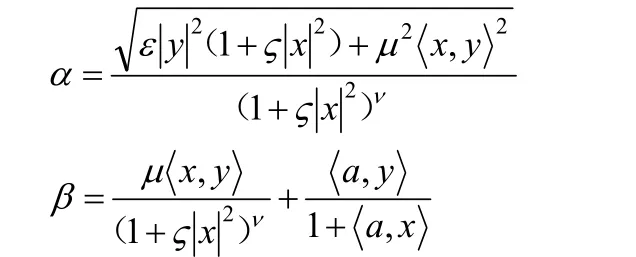
定理1 设 F =α+β为定义在Rn的开子集Ω上，其中α为Riemann度量，β为1-形式：那么 F =α+β为射影平坦的 Finsler度量的充分必要条件是ν=1，a∈v，且 μ2+ςε=0

证明 若 F =α+β射影平坦，即

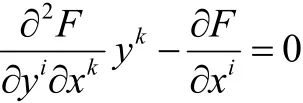
易证β为射影平坦的Finsler度量。

下面证α射影平坦的条件。令

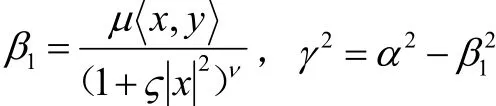
则

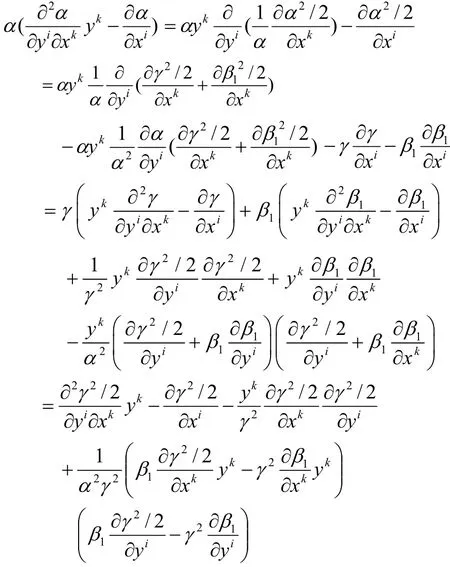
令

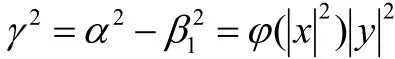
将

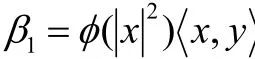
代入上式并化简

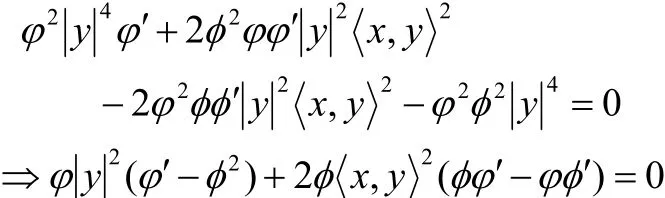
即

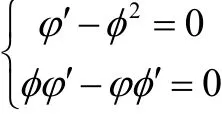
解此方程组得：

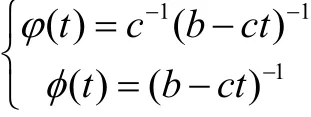
其中b, c为任意常数。

由于

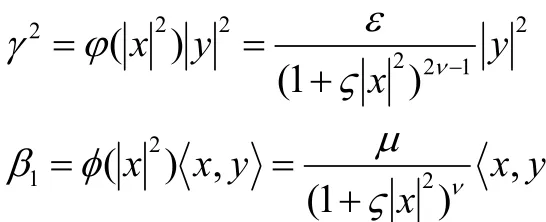
则可以解得当

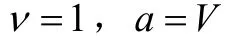
且

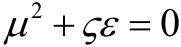
时，F为射影平坦的Finsler度量。

反之也可以证明。

3 旗曲率的计算

命题[4]任意一个局部射影平坦的 Finsler度量具有迷向旗曲率，此时旗曲率为

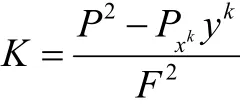
其中射影因子

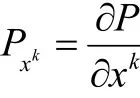
定理2 设 F =α+β为定义在Rn的开子集Ω上，其中α为Riemann度量，β为1-形式，当且具有如下形式：

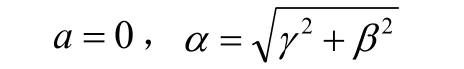
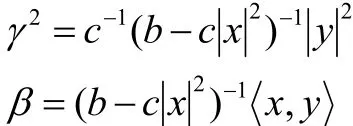
则F的旗曲率为

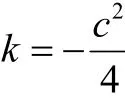
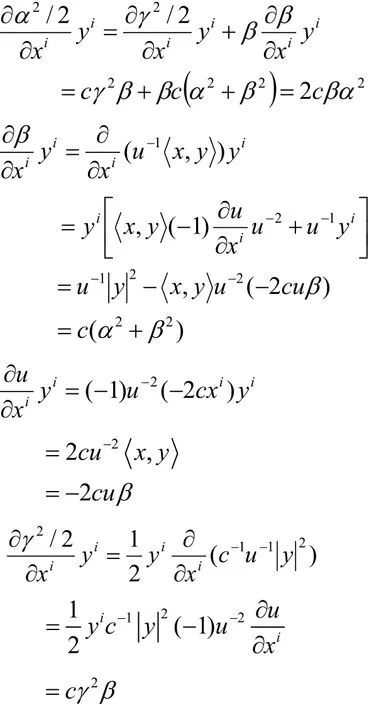
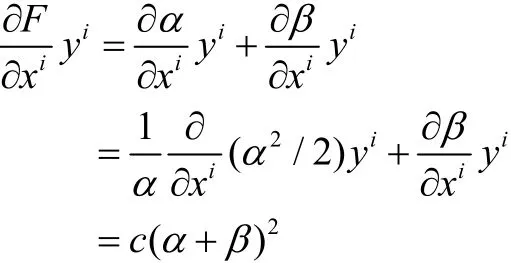
下面计算射影因子。

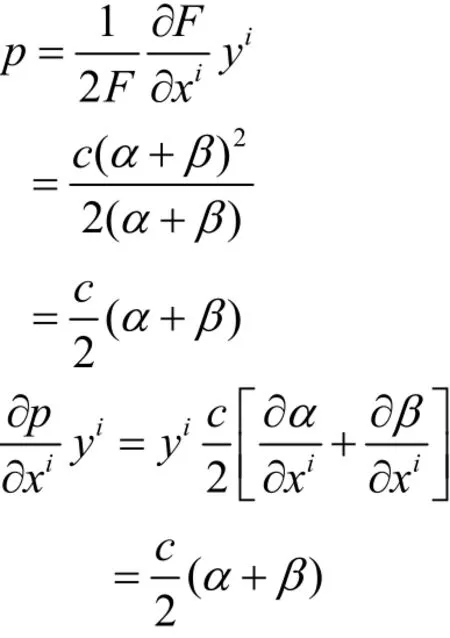
则

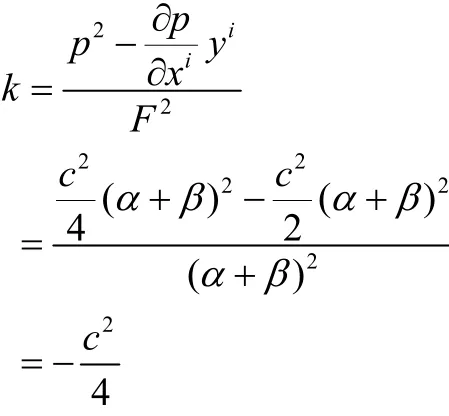
即旗曲率为

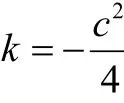
[1] X. Mo. An Introduction to Finsler Geometry[M]. Hackensack, NJ： World Scientific Publisher, 2006.

[2] Chen X, Mo X, Shen Z. On the flag curvature of Finsler metrics of scalar curvature[J]. J London Math Soc, 2003, 68(2)： 762-780.

[3] Shen Z. Projectivly flat Finsler metrics of constant flag curvature[J]. Trans of Amer Marh Soc, 2003, 355(4)： 1713-1728.

[4] Shen Z. Lectrues on Finsler Geametry[M]. Singapore：World Scientific Publishers, 2001.

[5] 杨春红.莫小欢.射影平坦的(α,)β度量的构造[J].内蒙古大学学报(自然科学版),2006,(6).

（责任编辑、校对：赵光峰）

Construction of a Kind of Special Projectively Flat (α, β) Metrics

XU Fei, ZHANG Gai-ping, ZHANG Huan

(Department of Basic Courses, The Academy of Armored Forces Engineering, Beijing 100072, China)

This paper constructs projectively (α,β) metric with 5-parametrers in the form of F =α+β, giving the condition of projectively flat and computing flag curvature.

(α, β) metrics; projectively flat metrics; finsler metrics; flag curvature

2010-10-07

许飞（1981-），男，河北张家口人，硕士，装甲兵工程学院基础部助教，研究方向为微分几何。

O186

A

1009-9115(2011)05-0004-03