探究2011年浙江省数学高考解析几何试题的来源及解法
2011-11-30诸暨市天马高级中学浙江诸暨311800
●(诸暨市天马高级中学 浙江诸暨 311800)
探究2011年浙江省数学高考解析几何试题的来源及解法
●王铁松(诸暨市天马高级中学 浙江诸暨 311800)
2011年浙江省数学高考理科卷的解析几何试题在直线方程表达上对学生的要求达到了前所未有的高度.笔者将对这一试题追根溯源并给出新的解法.
1 试题溯源

图1
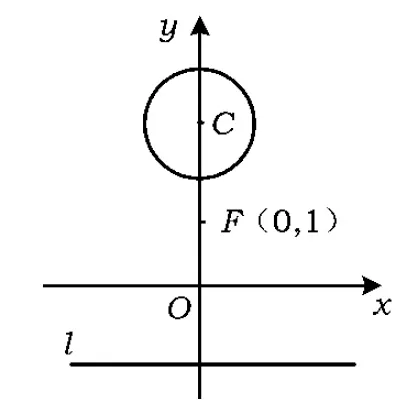
图2
例1如图1,已知抛物线C1:x2=y,圆C2:x2+(y-4)2=1的圆心为点M.
(1)求点M到抛物线C1的准线的距离;
(2)已知点P是抛物线C1上一点(异于原点),过点P作圆C2的2条切线,交抛物线C1于点A,B,若过点M,P的直线l垂直于AB,求直线l的方程.
(2011年浙江省数学高考理科试题)
本试题的雏形出现在1999年浙江省数学会考中:
例2如图2,已知点F(0,1),直线l:y=-2,及圆C:x2+(y-3)2=1.
(1)若动点M到点F的距离比它到直线l的距离小1,求动点M的轨迹E的方程.
(2)过轨迹E上一点P作圆C的切线,切点为A,B.要使四边形PACB的面积S最小,求点P的坐标及S的最小值.
(1999年浙江省数学会考试题)
会考卷的命题重心在于探究轨迹方程及通过圆几何关系的等价转换变为求动点到圆心距离的最小值,其对直线方程的要求几乎为零.
试题的另一个来源是2008年全国高中数学联赛试题:
例3如图3,P是抛物线y2=2x上的动点,点B,C在y轴上,圆(x-1)2+y2=1内切于△PBC,求△PBC面积的最小值.
(2008年全国高中数学联赛试题)

图3
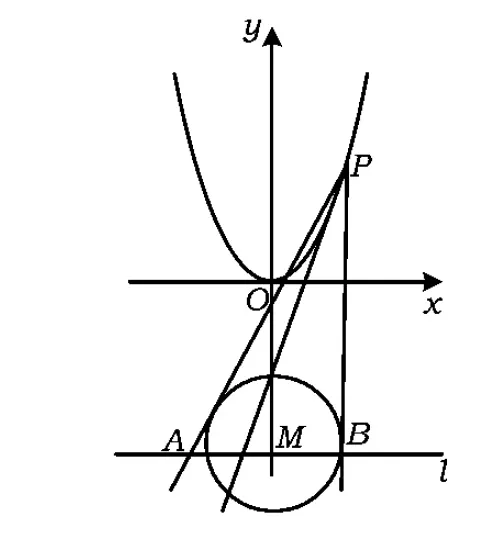
图4
例1与例3的不同点在于切线是与直线相交还是仍与抛物线相交,但都对从一点发出2条切线及其方程的表达上提出了较高要求.注意到在2011年浙江省数学高考文科卷中,命题者给出的也是与直线相交的问题,与例3同出一辙.
例4如图4,设P是抛物线C1:x2=y上的动点.过点P做圆C2的2条切线,交直线l:y=-3于点A,B.
(1)求C2的圆心M到抛物线C1准线的距离.
(2)是否存在点P,使线段AB被抛物线C1在点P处的切线平分,若存在,求出点P的坐标;若不存在,请说明理由.
(2011年浙江省数学高考文科试题)
2 试题求解
例1的解答有2种基本方案:
一是利用点斜式或直线方程的两点式写出切线方程,虽然是2条切线但可以用同一个形式来表示,这是此类问题的特点.
设P(t,t2),过点P的圆的切线斜率为k,则切线方程为y-t2=k(x-t).
由直线与圆相切得

从而
(t2-1)k2-2t(t2-4)k+(t2-4)2-1=0,
由韦达定理得
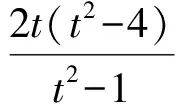
其中k1,k2为切线的斜率.
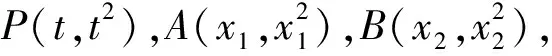
y-t2=(x1+t)(x-t).
由直线与圆相切得

从而
同理x2满足
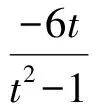
下面就是求出直线AB,PM的斜率,由2条直线垂直其斜率之积为-1建立关于t的方程即可.
上述的解法要求能预见到这样的一个一元二次方程存在,然后进行有效的表达和运算.
二是利用直线PM的位置关系进行解析.直线PM既是∠APB的平分线又满足与对边AB垂直,则△APB为等腰三角形,即点P位于线段AB的中垂线上,进而将问题转化为“中点与垂直”问题,进行更为简洁的解析如下:
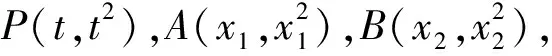
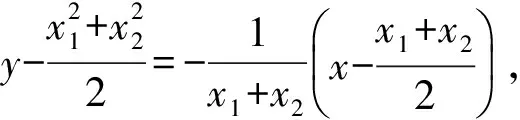
从而

也即直线PM的方程.
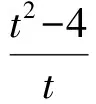
对比得到
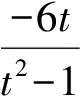
3 深刻反思
3.1 在解析几何复习中的解题教学
在解析几何复习中,关注较多的是经过某一点的直线,并在直线位置的变化中探究与曲线相交所产生的位置关系和数量关系.在解决此类问题时,学生对直线方程的挖掘与探究较少.其实,解析几何表达的精髓无非是坐标与方程,而方程的核心则是直线方程.曲线方程往往是已知的,而直线方程则要根据位置关系进行有效的表达.常见的情况有以下几种:经过一个定点、已知直线的方向、经过2个点、没有任何位置关系的信息,可以利用直线方程点斜式、斜截式和两点式来表示,还要有效地假设未知的信息,譬如引进斜率作为变量,或者同时引进斜率和截距作为变量.总之,直线及其位置关系只有通过方程才能展开运算,只有运算才能对几何关系进行有效的表达.
例1中从1个动点发出2条直线,学生可能想到用点斜式或结合与抛物线的另一个交点利用两点式来表示直线,但由于缺乏后面运算的预见性而不敢为.敢想却不敢为或者为而无所作为,这是考生中普遍存在的一个心理和能力上的障碍.笔者认为这与教学中存在的急功近利、教师单纯追求复习有效有一定关系,教师没有留出足够的时间让学生消化吸收,缺少真正的内化与落实.
3.2 如何更好地整合竞赛与高考资源
“高考试题竞赛化,竞赛试题高考化”,这是近几年命题中出现的一个新动向,尤其体现在名校的自主招生试题中.下面是近年来各级各类竞赛中出现的相关试题,供大家参考.
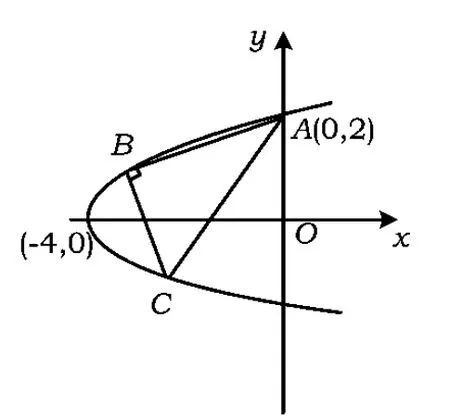
图5
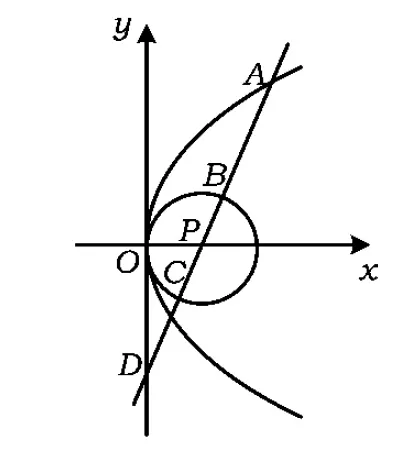
图6
1.如图5,已知点A(0,2)和抛物线y2=x+4上点B,C使得AB⊥BC,求点C的纵坐标的取值范围.
(2002年全国高中数学联赛试题)
2.如图6,给定圆P:x2+y2=2x及抛物线S:y2=4x,过圆心P作直线,此直线与上述2条曲线的4个交点自上而下顺次记为A,B,C,D.如果线段AB,BC,CD的长按此顺序构成一个等差数列,求直线l的方程.
(2006年江西省南昌市高中数学竞赛试题)
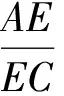
(2005年全国高中数学联赛试题)

(2009年全国高中数学联赛新疆预赛试题)

图7

图8
另外在一般的模拟卷中有以下相似试题.
5.如图9,过x轴上的动点A(a,0)向抛物线y=x2+1引2条切线AP,AQ,点P,Q分别为切点.
(1)若切线AP,AQ的斜率分别为k1,k2,求证:k1k2为定值;
(2)求证:直线PQ过定点;
(3)若a≠0,试求S△APQ:|OA|的最小值.
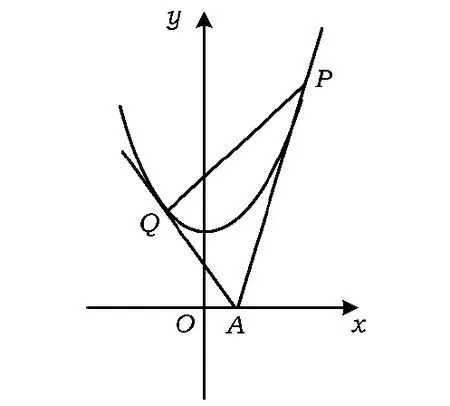
图9

图10
(1)求椭圆方程;
(2)如图10,过圆D:x2+y2=1上任意一点P引椭圆的2条切线m,n,求证:m⊥n.
7.设Q是直线y=-1上的一个动点,O为坐标原点,过点Q作x轴的垂线l,过点O作直线OQ的垂线交直线l于P.
(1)求点P的轨迹C的方程;
(2)过点A(-2,4)作圆B:x2+(y-2)2=1的2条切线交曲线C于点M,N,试判断并证明直线MN与圆B的位置关系.
