注重“一题多解、一题多变” 追求有效教学
——记一堂高三复习公开课及教学反思
2011-11-30台州中学浙江台州317000
●(台州中学 浙江台州 317000)
注重“一题多解、一题多变”追求有效教学
——记一堂高三复习公开课及教学反思
●毕里兵(台州中学 浙江台州 317000)
中学数学的课堂教学非常注重有效教学,无论是高一、高二的新课还是高三的复习课,有效教学都是热点和重点.课堂教学的40分时间如何高效、有效地发挥,这是一个难题.课堂的引入、问题的抛出、例题的讲解、习题的布置以及作业的合理选择等必须有效设计,才能让课堂有效.数学课堂教学的核心是培养学生的数学思维,高质量的数学课就必须注重数学的特征,尤其是在解题中注重连通性、变通性,才能让学生有所感有所悟.而要在这方面做得有效,笔者认为例题教学尤其是对应的变式教学非常重要.笔者有幸参加了当地高三数学有效性教学的公开课,就课堂教学中“如何才能更有效地让学生领悟数学思想,活用数学解题方法”,做了“一题多解、一解多题”与“一题多变、一变多题”教学方式的大胆尝试,受到了广泛好评,在此与读者共享.
1 案例回顾
和通常的复习课一样,本着“低起点、高要求”的目标,先抛出一个常见的有关二次函数恒成立的问题:
例1已知函数f(x)=x2+ax+3-a,a∈R.
(1)若f(x)≥0在x∈R上恒成立,求a的取值范围;
(2)若f(x)≥0在x∈[1,2]上恒成立,求a的取值范围.
(对于第(1)小题,学生利用一元二次不等式的解法可直接作答.)
1.1 函数思想
师:f(x)≥0在x∈[1,2]上恒成立等价于什么?
生:f(x)在[1,2]上时f(x)min≥0.
师:那么,如何求f(x)在[1,2]上的f(x)min呢?
生:利用对称轴与区间[1,2]的位置关系来分类讨论.
(以下过程由学生口述,教师板书.)
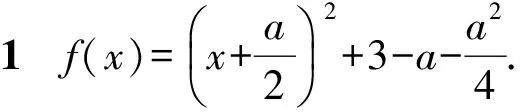
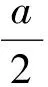
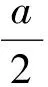
综上所述,a≥-7.
1.2 方程思想
解法2f(x)≥0在x∈[1,2]上恒成立即f(x)=0有且只有以下4种情况:
(1)无实根:Δ<0,即-6 (3)在(-∞,1]上有2个根: 故 a≥2. (4)在[2,+∞)上有2个根: 故 -7≤a≤-6. 综上所述,a≥-7. (学生甲刚说完,学生乙就站起来了.) 学生乙:可用参变分离方法. 1.3 参变分离方法 解法3f(x)≥0在x∈[1,2]上恒成立,故a(x-1)≥-(x2+3)在[1,2]上恒成立. (1)当x=1时,0≥-4恒成立,a∈R. (2)当x∈(1,2]时,不等式可化为 在x∈[1,2]上恒成立.又令 在x∈[1,2]上恒成立.故g(x)在[1,2]上递增,g(x)max=g(2)=-7,从而a≥-7. 综上所述,a≥-7. (此解法给出后,学生丙又站了起来.) 学生丙:a(x-1)≥(x2+3)在[1,2]上恒成立,画出不等式左、右2边函数的图像,从图像上可分析求解. 1.4 数形结合思想 解法4a(x-1)≥-(x2+3)在[1,2]上恒成立,在同一坐标系中作出图像 y1=a(x-1),y2=-(x2+3). 由题意知,函数y1=a(x-1)(1≤x≤2)的图像恒在函数y2=-(x2+3)(1≤x≤2)的图像上方. (1)当a≥0时,观察图像即得. (2)当a<0时,若y1=a(x-1)的图像与函数y2=-(x2+3)的图像相切,则 a(x-1)=-(x2+3),Δ=0, 故 a=-6或a=2(舍去), 当a=-6时,切点为(3,-12),不在考虑的定义域内. 要使函数y1=a(x-1)(1≤x≤2)的图像恒在函数y2=-(x2+3)(1≤x≤2)的图像上方,只要当x=2时,y1=y2即可,故a≥-7. 综上所述,a≥-7. (此法给出后,教师环顾四周,学生面面相觑,只听见一个学生在嘀咕.) 学生丁:若f(x)≥0的解集是A,则[1,2]⊆A. 1.5 集合观点 解法5(1)当Δ≤0,即-6≤a≤2时,不等式恒成立. (2)当Δ>0,即a<-6或a>2时,x2+ax+3-a≥0的解集是 要使f(x)≥0在x∈[1,2]上恒成立,只要 即 故 -7≤a<-6或a>2或a<-6. 综上所述,a≥-7. 其实这2个问题的设计入口很宽,看似普通,但能触动学生思维的火花,培养学生的数学思维品质,让学生在解决同一问题时各抒己见,让课堂引入变得十分有效. 1.6 变式演练 师:f(x)≥0在某个区间上恒成立,这又让我们想到了什么? 生:如果函数在某个区间上递增,它的导函数在这个区间上恒大于0. 师:非常好,利用这种关系,你能把条件改一下,变成另一个题吗? (学生分组讨论,最后形成以下3题.) 变式2已知函数f(x)=6x4+8ax3+12(3-a)x2+a+9在(0,+∞)上不单调,求a的取值范围. 变式3已知函数f(x)=[x3+(a+3)x2+(a+9)x+a+9]e-x,且f(x)≥f(2)对任意的x∈[1,2]都成立,求a的取值范围. 师:非常好,我们通过知识之间的联系,把原题变成了另一种形式.下面能否利用函数单调性的定义继续变题呢? 成立,求a的取值范围. 其实上述5个变式的设计,看似复杂,但是都可以通过适当变形、求导、移项等方式很快转化为课堂中的源问题.同时,让学生感受到“一题多解、一解多题”与“一题多变、一变多题”,这也使笔者最初的设计得到了有效尝试.课堂教学的有效性通过层层设计,不仅点燃了学生思维的火花,而且越烧越旺,为学生在解题和变题方面构建了知识基础,进一步培养了学生的数学思维品质. 笔者认为“一题多解”与“一题多变”是数学课堂有效教学重要的教学方式,它可以让学生在研究问题的过程中,领悟重要的数学思想和数学方法,灵活高效地解决数学问题. “一题多解”可训练思维的多向性.平时教学中要注意相关题型一般解法的指导,习惯称之为通法.学好通法,就能用一种解法去解决一类问题,这样既节约了时间,又最大限度地接触了诸多题目,可以达到“熟能生巧、以不变应万变”的效果.一题多解是开发智力、培养能力的一种行之有效的方法.进行思维分析,探讨阶梯规律和对习题的多角度追踪,能以少胜多地巩固基础知识,提高分析问题和解决问题的能力.掌握基本的解题方法和技巧,对沟通不同知识之间的联系、开拓思路、培养发散思维能力、激发学生的学习兴趣是十分有益的.例题教学中的解法1、解法2都属于通法,一般的学生都能想到,但是分类讨论容易疏忽,而解法3是在感觉分类讨论易错的前提下,想到参变分离法,此法可以避开分类讨论,得分会更高些,在解法3中注意发现的话,又产生了解法4.在课堂教学和复习中充满灵感、激情和理想的过程不能仅仅停留在习题本身文字信息所传达的通性通法,而是应该重视对已有解法的提炼、延伸,提高学生解题的灵活性,注重激发兴趣和求知欲,使课堂教学达到事半功倍的效果. “一题多变”可训练思维的变通性.利用“一题多变”构建新知识的最近发展区,寻找知识的生长点,引起学生的认知冲突,激发探究的热情,不断从一类问题引申到另一类问题,给学生的思维发展提供阶梯,让学生在探究中感悟知识、建构网络,这才能较大幅度地提高学生的学习效率.在例题教学中,如果注意到函数的单调性与导函数正负性的关系,就会思考:能否设计一个函数使其导函数就是原问题中的f(x),并且具有在[1,2]上递增性质的函数.因此有了变式1,而变式2、变式3都是单调性的不同表述而已.由高中教材函数单调性的定义,就有变式4、变式5.通过适当变换变化为多个与原题内容不同,但解法相同或相近的题目.“一题多变”有利于扩大学生视野,深化知识,举一反三,触类旁通,从而提高学生的解题能力,激发学生的学习兴趣,增强求知欲,提高课堂效率. 追求有效教学,教师必须重视研题的过程.只有教师的不断研究、不断反思,才能孕育教学智慧.笔者希望有一种反思文化,由此生成的教案才能真正体现教师的眼光、思想,由此进行的教学活动才能真正体现教师的创造,从而更好地走进学生的心灵,使课堂充满生命活力. [1] 罗增儒. 数学解题学引论[M].西安:陕西师范大学出版社,2008. [2] 罗增儒.中学数学解题的理论与实践[M].南宁:广西教育出版社,2008. [3] 波利亚.怎样解题:数学思维的新方法[M].上海:上海科技教育出版社,2007.
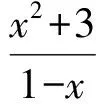
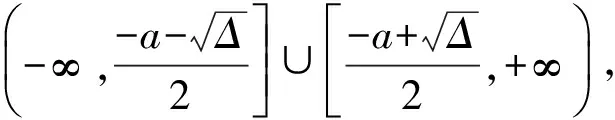
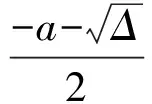
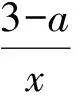
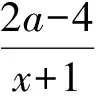
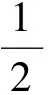
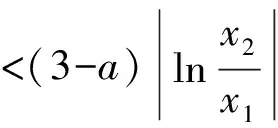
2 教学反思
