一个三角形面积关系式的再探究
2011-11-30常德市第六中学湖南常德415003
中学教研(数学) 2011年11期
●(常德市第六中学 湖南常德 415003)
一个三角形面积关系式的再探究
●彭世金(常德市第六中学 湖南常德 415003)
文献[1]研究了有心圆锥曲线涉及三角形面积的一个关系式,得到如下命题:


受其启发,笔者想到:如果线段AB是曲线Γ过中心的弦(不在轴上),那么上述结论是否还成立?通过探究,得到一个肯定的结果.


图1
证明如图1,连结OP,OQ,设M(x0,y0),A(m,n),B(-m,-n),则PQ,AP,BQ的方程分别为
(1)
(2)
(3)
式(1)-式(3),得OP的方程为
b2(x0-m)x+a2(y0-n)y=0,
因此

式(1)-式(2),得OQ的方程为
b2(x0+m)x+a2(y0+n)y=0,
因此

于是

因为点M(x0,y0),A(m,n)在椭圆上,所以
2式相减得

从而






令y0-n=-tb2(x0+m),x0-m=ta2(y0+n),则点M到AP的距离


点M到BQ的距离

从而

于是



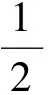
得

图2


性质2类似于性质1可证,此处从略.
[1] 梁鲁湘,姜坤崇.有心圆锥曲线涉及三角形面积的一个关系式[J].上海中学数学,2010(12):39.
