一道圆内接四边形面积最值高考题的研究

●(安康学院数学与应用数学研究所 陕西安康 725000)

一道圆内接四边形面积最值高考题的研究

●赵临龙(安康学院数学与应用数学研究所 陕西安康 725000)

在近几年数学高考试题中，有关圆内接四形边面积最值问题不断出现，人们对此开展了广泛讨论.

1 结论

2007年，田富德[1]给出了封闭二次曲线内接四边形对角线交点与直角坐标轴原点重合的四边形面积最大的结论.

2010年，周怡阳[2]结合2009年全国数学高考理科试题第16题，讨论了圆内接四边形对角线交点不与直角坐标轴原点重合的四边形面积最大值.现将此解法上升为一般理论.

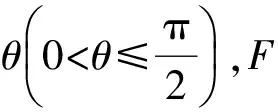
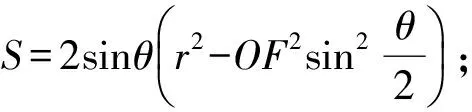
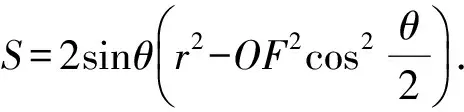
推论1若圆O：x2+y2=r2的内接四边形的对角线相互垂直，F为圆内一定点，则四边形面积最大值S=2r2-OF2.

但在实际中，往往是无法知道圆内接四边形对角线的夹角.因此，笔者[3]对圆内接四边形的对角线斜率形式作以讨论.

定理3若圆O：x2+y2=r2的内接四边形的对角线斜率分别为k1,k2(k1,k2≠0)，F为圆内一定点且|OF|=m>0,则四边形面积S是

推论3若圆O:x2+y2=r2的内接四边形的对角线相互垂直，F为圆内一定点且|OF|=m>0，则四边形面积S最值是

(1)当且仅当k1=1,k2=-1时,即OF平分四边形ABCD对角线AC，BD的交角时，四边形ABCD的面积取最大值S=2r2-m2；

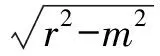
定理4若圆O：x2+y2=r2的内接四边形的对角线斜率k1,k2满足k1k2=-a(a>0且a≠1)，F为圆内一定点且|OF|=m>0,则四边形面积S最值是

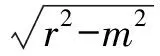
2 应用

(2009年全国数学高考理科试题)

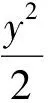
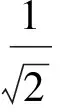
S椭圆四边形∶S椭圆=S圆四边形∶S圆，

即

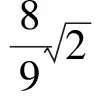
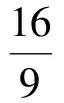
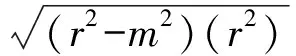
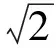
此时，由仿射变换知，当椭圆内接四边形的对角线斜率分别为0和∞时，四边形的面积取最大值2.

图1

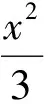
(2)求四边形ABCD面积的最小值.

(2007年全国数学高考理科试题)

解(1)略.

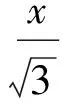
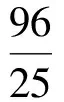
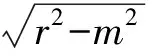
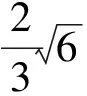
此时，由仿射变换知，当椭圆内接四边形的对角线斜率分别为0和∞时，四边形的面积取最大值为4.

有兴趣的读者，可以用此理论解决2007年安徽省数学高考文科试题：

例4设F是抛物线G：x2=4y的焦点.

(1)过点P(0，-4)作抛物线G的切线，求切线方程；

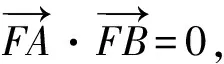
(此文为安康学院重点扶持学科《基础数学》建设项目(AZXZ0107)和安康学院高层次科研专项经费课题(AYQDZR201107)部分成果.)

[1] 田富德.封闭二次曲线内接四边形的面积最值问题[J]．数学教学，2007(11)：33-34.

[2] 周怡阳.探究一个圆内接四边形面积的最值[J].数学通讯，2010(Z3)：86-87.

[3] 赵临龙.圆内接四边形面积最值的理论研究[J].河南科学，2011(6)：643-647.

[4] 朱德祥.高等几何[M].北京：高等教育出版社，1983.