利用高斯伪谱法求解小推力伴星最优释放轨迹
2011-11-26段传辉董云峰
段传辉 董云峰
(北京航空航天大学宇航学院,北京100191)
1 引言
航天器编队飞行可以完成单个航天器所不能完成的任务,近年来成为国内外航天领域的研究重点[1]。
航天器相对运动轨迹控制是编队飞行的重要内容,传统方法一般以脉冲变轨完成。近年来由于小推力发动机技术逐渐成熟,以效率高、寿命长的特点得到充分的重视[2-4]。
求解航天器最优轨迹问题的方法通常可分为直接法和间接法[5-7],间接法利用Pontryagin原理,将最优控制问题转化为常微分方程的两点边值问题;间接法可以获得很高的精度,但是因初值猜测很困难,收敛半径小使得两点边值问题很难求解[5]。直接法的思想是将状态量和控制量离散化,将最优控制问题转化为非线性规划(NLP)问题,然后用常规的NLP求解方法,如系列二次规划方法(SQP)求得近似解。直接法有许多种,各种方法在计算量、收敛性等方面各有差异,近年来由David Benson和Huntington提出的高斯伪谱法对平滑型最优控制问题有很好的收敛性,以较少节点即可获得较高的精度[7-8]。国内的学者利用高斯伪谱法求解了深空探测、高超声速飞行器的再入、月球软着陆等最优轨迹问题[6,9-10]。
本文针对双星编队的伴飞星的释放任务,提出基于小推力变轨完成的从主星投放至形成稳定绕飞构型的燃料最省释放轨迹,利用高斯伪谱法将C-W方程描述的连续型最优控制问题转化为NLP问题,再利用SQP方法求解此NLP问题并给出了仿真算例。
2 相对运动描述及稳定绕飞条件
考虑目标航天器在圆轨道或者近圆轨道上运行,追踪航天器与目标航天器的位置误差远小于圆的半径,速度差远小于目标航天器的在轨运行速度。定义相对运动坐标系,其原点位于目标航天器质心,x轴指向速度方向,y轴指向目标飞行器矢径方向,z轴与x和y轴构成右手正交系。

式中A和B的定义为

考虑航天器不受轨控的绕飞情形,即令式(1)中T为零,可解出相对位置随时间的变化关系[11]为
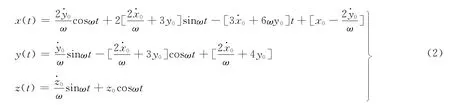
从式(2)可以看出,z方向和x,y是相互独立的,可单独分析。此外,三轴中仅x(t)中含有随时间线性增长的项为形成长期稳定的绕飞,则必须满足条件

此时,x-y平面内的方程可转化为
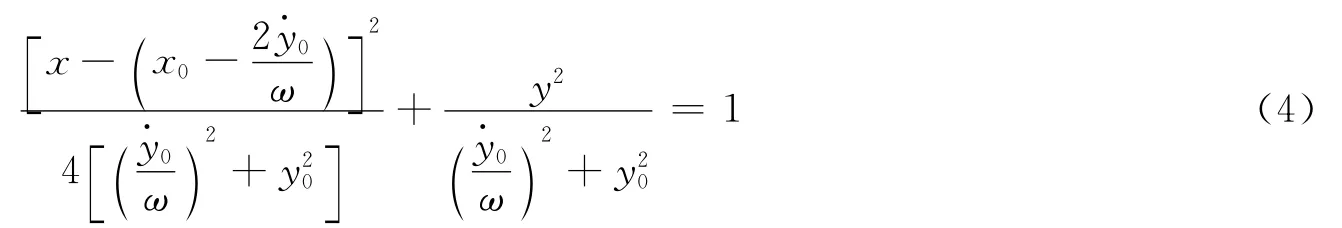
由此可见,飞行器的相对运动轨迹在x-y平面投影为一椭圆,其半长轴为半短轴为半长轴的一半,进一步分析可知,相对运动轨迹在y-z,x-z平面的投影也为椭圆,但其长轴和短轴不一定与坐标轴重合[12]。
上述椭圆的圆心在x轴还有常值偏移量,为达到伴星对目标星的较好观测效果,可进一步令

只要航天器的相对位置与相对速度初始条件满足式(3)和式(5),在近距离且不考虑摄动情况下,伴星相对目标星的轨迹为一个空间椭圆,且椭圆中心在目标星质心。
小型的伴星一般由主星搭载,入轨后通过航天员或者主星上的分离机构释放,初始相对位置Δr≈0,相对速度Δv≈0,此状态一般不满足式(3)和式(5)所确定的稳定的椭圆轨迹绕飞的初始条件,因此伴星投放后必须实施变轨,才能进入稳定的绕飞状态。
传统的变轨一般由脉冲控制来完成,只需进行有限次的脉冲即可进入目标轨道,此种方式计算简便,但是误差较大,不能精确调整。利用有限小推力发动机可以得到比脉冲控制更为精确的变轨,且可以充分利用已有的最优控制理论,对变轨过程进行优化。本文选用推力恒定,方向可变的常值小推力发动机完成伴星的释放轨迹控制,则关于求解推力器喷气方向单位矢量u=[ux,uy,uz]T的最优控制问题可描述如下。
边界点约束:x(t0)=[r0,v0],x(tf)=[rf,vf],在初始状态选取时注意刚释放时r0≈0,v0≈0,在终端时刻,即变轨结束点(椭圆绕飞构型的入口点处),rf一般取为102m~103m的级别,而vf是根据rf的取值及式(3)和式(5)的约束条件来确定的。
过程约束:由于控制量u是方向矢量,必须满足
3 高斯伪谱法求解最优控制问题
高斯伪谱法的基本思想是通过将随时间连续变化的状态量和控制量在有限个数的时间点进行离散,用这些离散点上Lagrange差值多项式近似表达状态量和控制量函数,再利用Gauss数值积分将积分约束转化为代数求和约束,最终将最优控制问题转化为NLP问题来求解。
设x(t)∈Rn为状态变量,u(t)∈Rm为控制变量,t0和tf为起始和结束时刻,则一个典型的Bolza型的最优控制问题[8]可描述为确定u(t),使以下指标函数为最小。
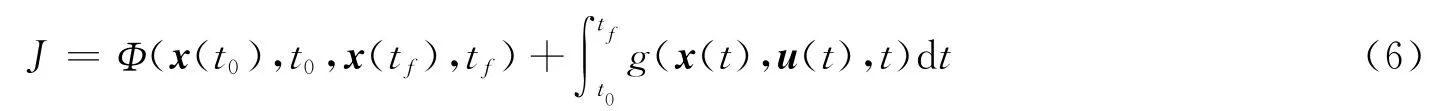
式中Φ为终端指标;g为积分型指标。式(6)中各变量满足以下约束

式中ψ为等式约束;C为不等式约束。由于Gauss积分定义在[-1,1],需将以上t∈[t0,tf]描述变换为τ∈[-1,1],变换方法为

对于一个定义在[-1,1]上的函数f(t),取Legendre-Gauss多项式的K个零点(LG点)τ1~τK,则可利用Gauss积分公式将积分求解转化为近似求和运算
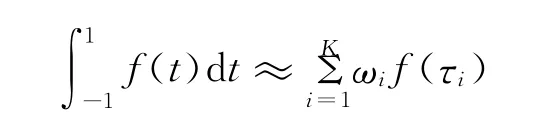
式中ωi为第i处的高斯权重,ωi和τi只与个数K有关,求解方法参见文献[7]。
利用起始点τ=-1及K个LG零点共计K+1个点,对x(t)进行K+1次多项式Lagrange差值[8]得到:
Lagrange差值可以保证在K+1个差值点处有x(τi)=X(τi),其他点处二者则近似相等。
同理,对u(t)在K个LG零点处进行Lagrange差值(因差值点个数不同


式中Dki为微分矩阵,仅与LG点的个数K有关,可在算法开始前离线确定,其定义[8]为
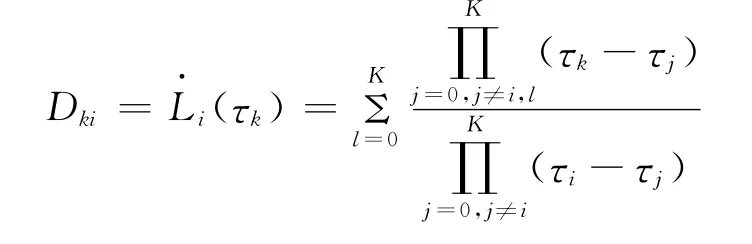
针对伴星释放最优轨迹控制的具体问题,设起始时刻t0=0,状态变量为x=[x,y,z,vx,vy,vz]T,控制变量为推力器方向矢量u=[ux,uy,uz]T,动力学微分方程的右端函数为f(x,u)。将连续量的x(τ)和u(τ)在[-1,1]区间进行离散,其中x(τ)的离散点取为起始点、终止点及K个LG点,构成一个6(K+2)维的未知向量[X0,X1,…,XK,Xf],控制量u(τ)的离散点选取在K个LG点处,构成一个3K维的未知向量[U1,U2,…,UK]。
根据高斯伪谱法,离散变换之后,连续型的最优控制问题的微分方程约束可化作6K维的代数约束Rk,其表达式为
边界条件为ψ(x(t0),t0,x(tf),tf)=0,即上文所述的释放初始及结束时刻的位置、速度应满足的条件,其维数为12。
过程约束为C(Xk,Uk,τk,tf)≤0,(k=1,2,…,K),即每个LG点处Uk模为1的条件,其维数是6K。
指标函数为min(J),J=tf。
至此,伴星释放最优控制问题转化为针对9K+13维的未知量Y=[X0,…,XK,Xf,U1,U2,…,UK,tf],在满足Rk=0,Rf=0,ψ=0,C≤0条件下的一个非线性规划问题,可用现有的非线性规划问题求解方法进行求解,本文选用效率比较高的系列二次规划法求解。
由于高斯伪谱法求解得到的控制量是有限点处的近似解,而完整的控制问题需要知道任意时刻的控制量,本文选用三次样条差值法在所求解得到的离散点处的控制量[U1,U2,…,UK]上进行差值,以此获得控制量在整个时间历程上随时间连续变化的函数u(t)。
4 仿真算例
考虑目标飞行器轨道高度为h=500km的圆轨道,伴星质量m=200kg,推力器推力T=1N,高斯伪谱法计算节点K=100,起始点的相对位置x,y,z为2m,相对速度Vx,Vy,Vz为0.01m/s。
终端时刻的伴星在主星的轨道坐标系下的位置即椭圆绕飞入口的坐标为[1 000m,600m,-500m],终端时刻的vx和vy可由式(3)和式(5)的绕飞条件来确定,再设vz=vy,则终端的位置和速度完全确定。
在Matlab环境下,高斯伪谱法建模的开源软件包GPOPS将最优控制问题转化为NLP问题,最终转化出的NLP再用基于SQP的SNOPT[13]求解器来完成求解。在SNOPT中迭代575次,最终求解得到伴星释放过程持续时间tf=1 179.1s。图1~图3分别为释放过程中的控制量、相对位置、相对速度随时间的变化曲线。
从图1可以看出,整个变轨过程中除y方向控制量有一个较小尖峰之外,基本上是一个平滑的变化过程,这种平滑的变化易于推力器的实现。从图2和图3可以看出两个航天器的相对距离、速度从开始释放时基本为零,平稳地过渡到稳定椭圆绕飞的要求值,没有出现较大的波动。
图4是伴星从释放到稳定的围绕主星飞行20天的三维轨迹,可见卫星经过最优变轨控制,顺利进入预定的椭圆绕飞轨道。由于在变轨结束时刻的相对位置和相对速度与椭圆绕飞所需的值之间仍有误差,造成x轴方向仍有常值漂移项,按照所求解出的离散控制量进行三次样条差值,积分相对运动方程所得到tf时刻的相对位置和速度为x=1 000m,vy=0.553 41m/s,则由式(3)得到的x方向常值飘移速率为3vx+6ωy=-6.275×10-5m/s,随着时间推进,绕飞曲线将逐步偏离预设轨道。实际上,即使变轨过程完全没有误差,在摄动力作用下,伴星相对运动轨道也将逐步飘移,要完成稳定的绕飞,需要不断地进行轨道修正。本文仅考虑释放轨迹的最优控制,对绕飞保持控制问题不做讨论。

图1 控制量的时间历程Fig.1 Result of control

图2 相对位置时间历程Fig.2 Result of relative position
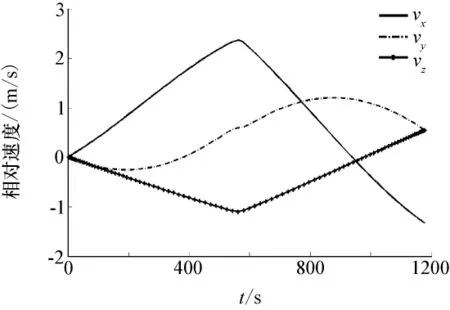
图3 相对速度的时间历程Fig.3 Result of relative velocity

图4 释放与绕飞三维轨迹Fig.4 3Dfigure of releasing and around-flight orbit
5 结束语
本文利用高斯伪谱法,以无控的椭圆绕飞构型为最终目标,求解了小推力伴星的最优释放轨迹,仿真算例表明高斯伪谱法无需对状态量和控制量给出较好的猜测即可收敛,根据其求解出的离散控制量进行拟合后得到的连续控制量能够让状态变量控制到指定值。
[1]张育林,曾国强,王兆魁,等.分布式卫星系统理论及应用[M].北京:科学出版社,2008:3-11.ZHANG YULIN,ZENG GUOQIANG,WANG ZHAOKUI,et al.Theory and application of distribute satellite system [M].Beijing:Science Press,2008:3-11.
[2]顾大可,段广仁,张卯瑞.有限推力交会的最省燃料轨迹[J].宇航学报,2010,31(1):75-81.GU DAKE,DUAN GUANGREN,ZHANG MAORUI.Fuel-optimal trajectories for finite-thrust rendezvous[J].Journal of Astronautics,2010,31 (1):75-81.
[3]师鹏,李宝军,赵育善.有限推力下的航天器绕飞轨道保持与控制[J].北京航空航天大学学报.2007,33(7):757-760.SHI PENG,LI BAOJUN,ZHAO YUSHAN.Orbital maintenance and control of spacecraft fly-around with finite-thrust[J].Journal of Beijing University of Aeronautics and Astronautics,2007,33 (7):757-760.
[4]吴文华,曹喜滨,张世杰,等.编队卫星相对轨道与姿态一体化耦合控制[J].南京航空航天大学学报,2010,42 (1):13-20.WU WENHUA,CAO XIBIN,ZHANG SHIJIE,et al.Relative orbit and attitude integrated coupled control for formation satellite[J].Journal of Nanjing University of Aeronautics & Astronautics.2010,42 (1):13-20.
[5]周文雅,杨涤,李顺利.利用高斯伪谱法求解具有最大横程的再入轨迹[J].系统工程与电子技术,2010,32 (5):1039-1042.ZHOU WENYA,YANG DI,LI SHUNLI.Solution of reentry trajectory with maximum cross range by using Gauss pseudospectral method[J].Systems Engineering and Electronics,2010,32 (5):1039-1042.
[6]尚海滨,崔平远,徐瑞,等.基于高斯伪光谱法的星际小推力转移轨道快速优化[J].宇航学报,2010,31 (4):1005-1011.SHANG HAIBIN,CUI PINGYUAN,XU RUI,et al.Fast optimization of interplanetary low-thrust transfer trajectory based on Gauss pseudospectral algorithm [J].Journal of Astronautics,2010,31 (4):1005-1011.
[7]DAVID BENSON.A Gauss pseudospectral transcription for optimal control[D].Cambridge:Department of Aeronautics and Astronautics,MIT,2004.
[8]HUNTINGTON GEOFFREY TODD.Advancement and analysis of a Gauss pseudospectral transcription for optimal control problems[D].Cambridge:Department of Aeronautics and Astronautics,MIT,2007
[9]雍恩米,唐国金,陈磊.基于Gauss伪谱法的高超声速飞行器再入轨迹快速优化[J].宇航学报,2008,29 (6):1766-1772.YONG ENMI,TANG GUOJIN,CHEN LEI.Rapid trajectory optimization for hypersonic reentry vehicle via Gauss pseudospectral method [J].Journal of Astronautics,2008,29 (6):1766-1772.
[10]彭祺擘,李海阳,沈红新.基于高斯伪谱法的月球定点着陆轨道快速优化设计[J].宇航学报,2010,31 (4):1012-1016.PENG QIBO,LI HAIYANG,SHEN HONGXIN.Rapid lunar exact-landing trajectory optimization via Gauss pseudospectral method[J].Journal of Astronautics,2010,31 (4):1012-1016.
[11]刘暾,赵骏.空间飞行器动力学[M].哈尔滨:哈尔滨工业大学出版社,2003:83-89.LIU TUN,ZHAO JUN.Spacecraft dynamics[M].Harbin:Press of Harbin Institute of Technology,2003:83-89.
[12]肖业伦.航空航天器运动的建模[M].北京:北京航空航天大学出版社,2003:118-122.XIAO YELUN.Model of aircraft and spacecraft dynamics[M].Beijing:Beihang University Press,2003:118-122.
[13]GILL PHILIP E,MURRAY WALTER,SAUNDERS MICHAEL A.SNOPT:an SQP algorithm for large-scale constrained optimization [J].SIAM Journal on Optimization,2002,12 (4):979-1006.
