基于扩张状态观测器的航天器自适应姿态控制
2011-11-26袁国平史小平李隆
袁国平 史小平 李隆
(哈尔滨工业大学控制与仿真中心,哈尔滨150001)
1 引言
目前,许多空间任务(例如对地观测)要求航天器具有良好的姿态机动性能。航天器迅速、精确地完成机动任务可以增加其使用范围,获得更多的有用信息。但航天器在姿态机动中滚转、俯仰和偏航三轴运动相互耦合影响,是一个典型的非线性问题,控制器综合难度大。另外,航天器在运行期间,不可避免地会受到各种环境力矩的干扰。同时,航天器执行部件安装误差等因素造成输出力矩的偏差也会影响姿态控制精度。因此,寻求一种控制律使航天器能够在各种不确定性下快速完成姿态机动任务成为研究热点之一。
自抗扰控制器(ADRC)是一种几乎不依赖于受控对象模型的非线性控制算法,具有良好的鲁棒性和处理非线性问题的能力。它包含跟踪微分器,扩张状态观测器(ESO)和非线性反馈等技术[1-3]。作为核心技术的扩张状态观测器,除能够对系统状态进行观测外,还能精确地估计出系统的非线性及外界干扰信息,在航天器控制研究中得到了广泛的应用。文献[4]将ADRC应用于带挠性太阳翼的航天器偏航轴的姿态稳定控制。文献[5]提出了一种双闭环的ADRC,利用该算法实现挠性航天器的高精度姿态稳定控制。文献[6]利用ADRC研究了三通道的姿态机动控制问题,并对控制器参数进行了整定。文献[7]针对柔性多体航天器,利用自抗扰算法,实现了姿态稳定控制。文献[8]将ESO和模糊自适应控制相结合,设计了带转动部件的挠性卫星的姿态稳定控制算法。
针对航天器的姿态机动问题,本文利用ESO能够准确地获取航天器三轴间非线性耦合及其他未知外界干扰信息的能力,设计了一种仅需要姿态角测量值的自适应输出反馈控制律;在此基础上,利用Lyapunov方法对系统的稳定性进行了分析;最后,将提出的方法应用于航天器多轴同时机动的姿态控制问题。
2 模型的建立
本文考虑的航天器近似为刚体,由动量矩定理,可将其动力学方程写成

式中J=diag(JxJyJz)为沿航天器本体主惯量轴的转动惯量矩阵;ω=[ωxωyωz]T是航天器相对惯性坐标系的瞬时转速在本体坐标系中的矢量;u(t)=[uxuyuz]T为控制力矩矢量;d(t)=[dxdydz]T为作用在星体上的外干扰力矩矢量。定义斜对称矩阵S(ω)为

采用3-1-2转序的欧拉角描述航天器的姿态,其运动学方程为
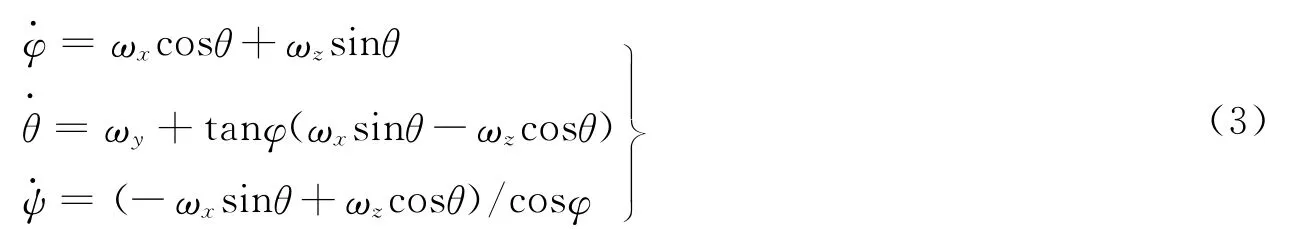
式中φ,θ,ψ分别为航天器的滚转、俯仰和偏航角。
由式(1)和式(3)可知,当航天器进行大角度机动时,其动力学方程是耦合非常强的非线性系统,直接利用非线性理论进行控制器综合的难度很大。这时,可以把复杂的动力学模型分成3个子通道,即滚转通道、俯仰通道和偏航通道[8-9]。
2.1 滚转通道模型

2.2 俯仰通道模型

2.3 偏航通道模型

通过公式(4)~(6)可以看出,航天器的3个通道之间通过非线性项fx2、fy2、fz2耦合在一起,特别当航天器进行大角度机动时,耦合非常强烈。因此,在设计3个通道控制器时,应充分考虑各个子系统之间的耦合。ESO不仅可以对系统中的非线性项进行精确的估计,并且还可以通过扩张状态观测估计不可测的状态,降低任务成本。因此,本文设计的航天器姿态机动控制器,3个通道均采用基于ESO的自适应控制算法,从而能够有效地克服各通道的相互耦合。
航天器的姿态机动问题可以转换为姿态跟踪控制,首先根据任务设计系统姿态机动的指令,然后通过控制系统使航天器的状态向量x(t)去跟踪一个目标状态向量xd(t),其中xd(t)=[xd(t),跟踪误差可以写成如下的形式
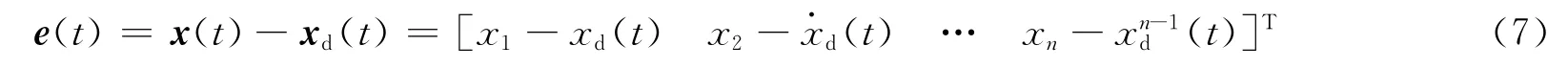
则控制的目标转化为设计一个自适应控制器使跟踪误差渐近趋近于0。
3 ESO的设计
在实际的航天任务中,使用高精度的角速率陀螺会提高系统的设计成本,在研制经费有限的情况下,可以考虑不安装;另一方面,若速率陀螺失效,就将无法获得角速度信息。故无论是从降低航天器研制成本,还是从作为角速率陀螺失效备份的角度来看,通过观测器获得速率信息不失为一个很好的选择。另外,系统中fx2、fy2、fz2这样的非线性耦合特性往往很难精确获得。为此,本节中在只有姿态角可测的情况下,利用ESO估计出系统的其他状态和未知的非线性耦合项。
下面以航天器的滚转通道为例,介绍扩张状态观测器的设计方法。

可将xx3=fx2看成总的干扰项,其中包含了其他两通道到滚转通道的耦合,外界的干扰力矩和其他未建模动态等。
取ex3=xx3,由式(7)和式(8)可得系统的误差状态方程为
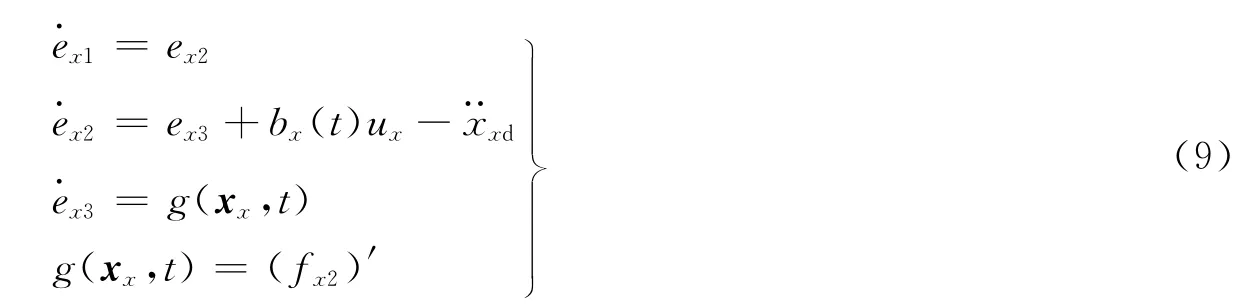
根据式(9)的形式,构造三阶的ESO[1]
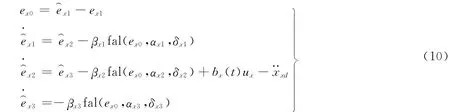
式中 fal(e0,α,δ)为在原点附近有线性段的非线性函数
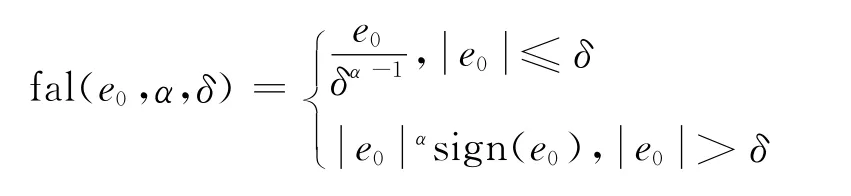
在ESO中,只要合理适当的选择参数βx1,βx2,βx3,并保证观测器中的系数α>0,0<δ<1,则观测器公式(10)就能很好地估计系统公式(9)的所有状态变量,且满足稳定性条件,最终达到如下的稳态
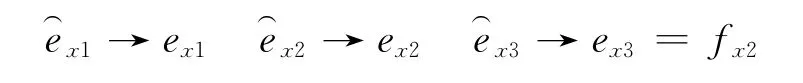
即ESO可以实时地估计出总的干扰项fx2。
由公式(5)、(6)可以看出,变换后的俯仰和偏航通道的状态方程与滚转通道有相似的形式,利用与上面相同的方法,可建立这两个通道的ESO,具体过程不再详述。
4 自适应控制器设计
由前面的叙述可知,航天器大角度机动问题可转化为:给定航天器的初始姿态和期望姿态,设计两姿态之间的运动轨迹,通过控制器使航天器跟踪期望轨迹机动到期望姿态,并最终使系统稳定在期望的平衡状态附近。
另外,考虑到控制力矩输出可能存在偏差,设计自适应律对这一偏差进行在线估计。同时为了保证估计值有界,本文采用了基于投影算子的自适应律,整体的控制结构框图如图1所示。
同样考虑到三通道控制器的相似性,在这里也以滚转通道为例来介绍控制器的设计过程。
定理 给定常数ν>0,λ>0,采用如下的自适应控制器
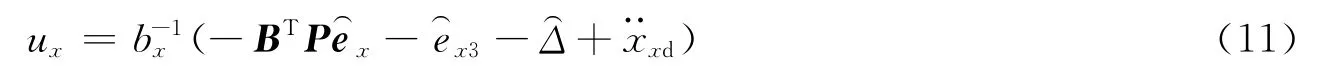
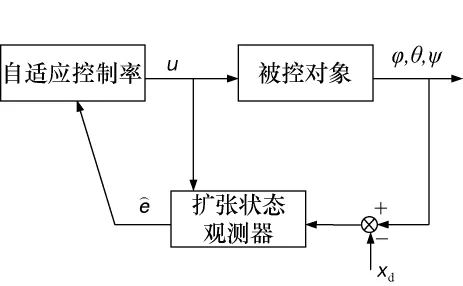
图1 控制系统结构框图Fig.1 Control system structure
和参数更新律

保证滚转通道公式(4)的姿态跟踪误差渐近趋于0,即xx→xxd。其中P为满足如下矩阵不等式的对称正定阵
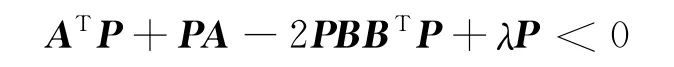
为控制力矩偏差Δ的估计值,为估计误差,即投影算子的具体定义[10]:

取Lyapunov函数

对公式(13)求导可得
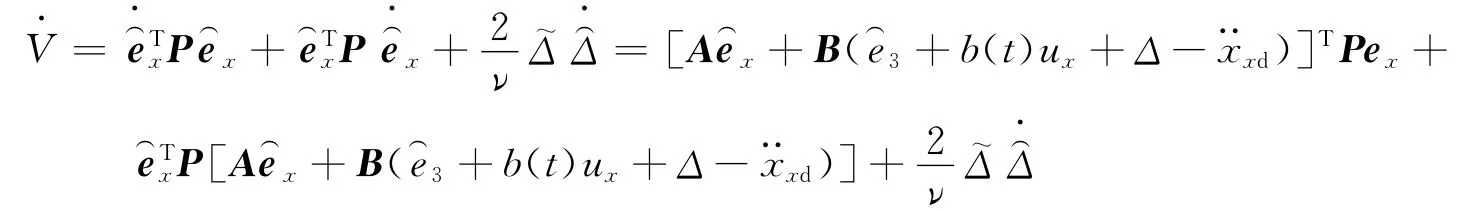
将控制率公式(11)代入,整理后得到
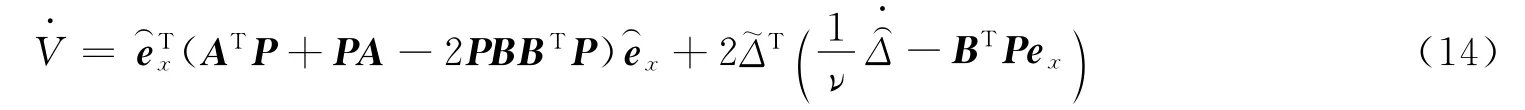
由自适应律公式(12)可得

对于任取的自适应律η,投影算子可以保证如下的性质[10]
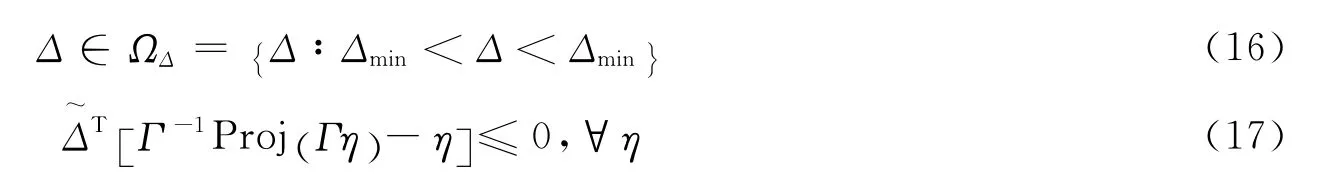
把公式(15)代入公式(14),再由投影算子性质公式(17),可得
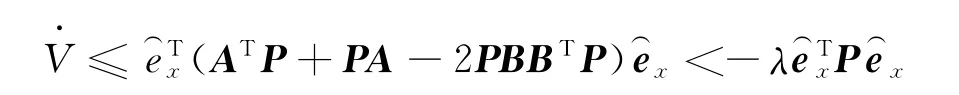
因为矩阵P正定,显然由稳定性理论可知系统的跟踪误差渐近趋于零,即xx→xxd。
偏航和俯仰通道可利用类似的方法得到控制器,最终得到三通道控制器:
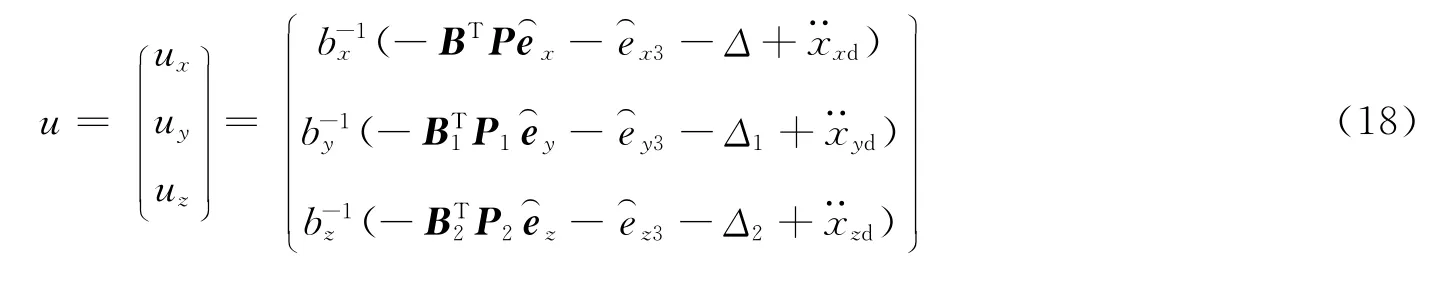
5 仿真分析
针对本文提出的基于ESO的控制方法,本节通过数字仿真来研究其在航天器大角度机动中的效果。航天器转动惯量

本文设计的控制器中需要姿态机动目标跟踪指令及其前两阶导数,为了保证系统的统一和可实现性,航天器三个姿态角的机动指令均有图2所示的系统产生。其中为姿态机动的目标值,分别为姿态机动指令、指令的一阶导数和二阶导数。
为了比较,文中设计了三组仿真试验对控制器的性能进行检验:1)滚转轴单独机动,其他两通道保持在稳定状态;2)滚转轴和偏航轴同时机动;3)三轴同时机动并且存在控制转矩输出误差。
第1组仿真试验的结果如图3和图4所示。试验中采用本文提出的方法实现了航天器滚转轴30°的姿态机动,从姿态角、角速度、控制力矩的仿真曲线中(见图3)可以看到,滚转轴机动到位的时间约为25s,偏航和俯仰轴的姿态角都趋于0°,控制力矩变化也很平稳。另外,由图4可以看出,ESO对航天器姿态角及角速率与控制指令之间的偏差都可以进行很好的估计,此跟踪误差在25s时渐近趋于零,这也反映了在控制器的作用下,姿态角精确地跟踪了参考指令。当只有单轴机动时,由动力学模型可知,航天器的三个姿态角之间的耦合并不是很严重,因此为了验证方法的有效性,还需要进行多轴同时机动的试验。
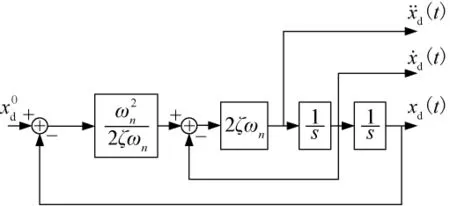
图2 指令生成系统Fig.2 Command generator

图3 三轴姿态角、角速率及控制力矩响应曲线(滚转轴机动)Fig.3 Responses of attitude angles,rates and control torques(roll axis maneuver)
图4 三轴姿态角、角速率跟踪误差估计(滚转轴机动)Fig.4 Estimates of attitude angle,rate tracking errors(roll axis maneuver)
第2组试验的结果如图5和图6所示。在控制器作用下,航天器的滚转和偏航轴在同一时间段内分别进行了20°和60°的大角度机动。从图中可以看到,偏航轴在50s左右机动到位,姿态角速率和控制力矩变化很平缓。图6给出的估计误差最终收敛于0,表明观测器在两轴同时机动时仍然能够保持优良的性能。另外,这也说明在基于ESO的控制律的作用下,航天器很好地完成了多轴机动的任务。由于执行器安装误差等原因,其输出力矩可能与期望值存在偏差,从而影响航天器的控制精度。在前两个试验中并没有考虑这一因素,为了验证采用自适应律的控制方案抑制这类误差的有效性,本文设计了第3组仿真试验。

图5 三轴姿态角、角速率及控制力矩响应曲线(双轴机动)Fig.5 Responses of attitude angles,rates and control torques(two-axis maneuver)
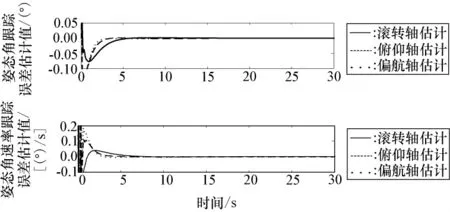
图6 三轴姿态角、角速率跟踪误差估计(双轴机动)Fig.6 Estimates of attitude angle,rate tracking errors(two-axis maneuver)
图7 ~图9给出了第3种情况的结果。在整个仿真过程中,航天器三轴的执行部件上作用有[Δx,Δy,Δz]T=[0.05,0.02,-0.03]TN·m的常值偏差力矩,航天器的滚转、俯仰和偏航三轴在同一时间段内分别进行了60°、20°和40°的机动,在约50s时三轴均机动到指定角度。图9给出了基于投影算子的自适应律对力矩偏差的估计结果,从图中可知,算法较好地完成了任务,估计值均在设定的范围之内,最后趋近于设定的误差。由于本文提出的控制律主动考虑了执行机构的输出力矩偏差,并且自适应控制算法具有良好的辨识性能,再加上ESO处理非线性的优势,使三轴耦合和力矩偏差对航天器机动性能的影响减少,提高了航天器的控制精度。
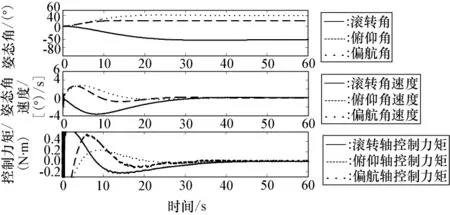
图7 三轴姿态角、角速率及控制力矩响应曲线(三轴机动)Fig.7 Responses of attitude angles,rates and control torques(three-axis maneuver)
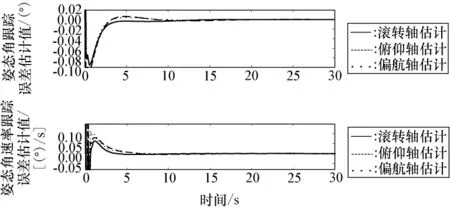
图8 三轴姿态角、角速率跟踪误差估计(三轴机动)Fig.8 Estimates of attitude angle,rate tracking errors(three-axis maneuver)
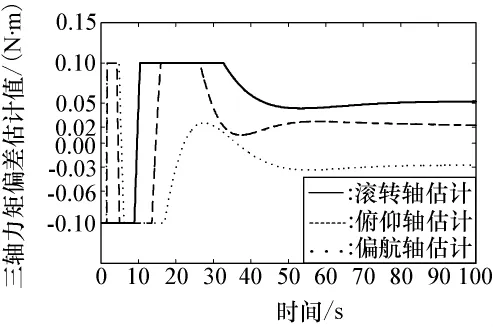
图9 控制力矩偏差估计Fig.9 Estimates of control torque errors
6 结束语
本文利用扩张状态观测器设计了一种仅需要姿态角测量值的自适应输出反馈控制律。研究表明,基于扩张状态观测器的自适应控制器在解决存在非线性耦合和干扰的控制问题时能够取得很好的效果。系统抗干扰能力增强,响应速度加快,同时算法具有较强的鲁棒性。
仿真试验表明,利用本文设计的控制器能够保证航天器完成多轴同时姿态机动的任务。但是,扩张状态观测器涉及的参数较多,需要进一步研究参数的整定和优化方法。同时,若能将本文的方法与其他诸如容错控制等方法相结合,必将会有很好的研究前景和价值。
[1]韩京清.从PID技术到 “自抗扰控制”技术[J].控制工程,2002,9(3):13-18.HAN JINGQING.From PID to active disturbance control[J].Control Engineering,2002,9(13):13-18.
[2]黄一,张文革.自抗扰控制器的发展[J].控制理论与应用,2002,19(4):485-492.HUANG YI,ZHANG WENGE.Development of active disturbance rejection controller[J].Control Theory and Applications,2002,19 (4):485-492.
[3]黄一,韩京清.非线性二阶连续扩张状态观测器的分析与设计[J].科学通报,2000,45(13):1373-1379.HUANG YI,HAN JINGQING.Analysis and design for the second order nonlinear continuous extended states observer[J].Chinese Science Bulletin,2000,45 (13):1373-1379.
[4]雷仲谋,吕振铎.非线性自抗扰控制器在航天器姿态控制系统中的应用[J].航天控制,2000,18(4):34-39.LEI ZHONGMOU,LV ZHENDUO.Nonlinear auto-disturbance rejection controller for spacecraft attitude control system [J].Aerospace Control,2000,18 (4):34-39.
[5]朱承元,杨涤,翟坤.无陀螺大挠性多体卫星的自抗扰姿态控制[J].计算机仿真,2005,22(1):43-47.ZHU CHENGYUAN,YANG DI,ZHAI KUN.Active disturbance rejection attitude controller for large flexible multi-body satellite without gyroscopes [J].Computer Simulation,2005,22(1):43-47.
[6]周黎妮,唐国金,李海阳.航天器姿态机动的自抗扰控制器设计[J].系统工程与电子技术,2007,29(12):2122-2126.ZHOU LINI,TANG GUOJIN,LI HAIYANG.Active disturbance rejection controller design for spacecraft attitude maneuver[J].Systems Engineering and Electronics,2007,29 (12):2122-2126.
[7]李顺利,李立涛,杨旭.柔性多体航天器自抗扰控制系统的研究[J].宇航学报,2007,28(4):845-849.LI SHUNLI,LI LITAO,YANG XU.Active disturbance rejection control for flexible multi-body satellite system [J].Journal of Astronautics,2007,28 (4):845-849.
[8]WANG ZUOWEI,GUO JIANXIN,HE YINGZI.Spacecraft attitude control based on extended state observer and fuzzy logic system [C].Proceedings of the 2009IEEE International Conference on Mechatronics and Automation,Changchun,China,August 9-12,2009:3894-3899.
[9]周荻,暮春棣,徐文立.空间拦截器姿态的组合控制[J].清华大学学报,1999,39(1):106-109.ZHOU DI,MU CHUNDI,XU WENLI.Integrated control for space interceptor′s attitude [J].Journal of Tsinghua University,1999,39 (1):106-109.
[10]XU LI,YAO BIN.Output feedback adaptive robust precision motion control of linear motors[J].Automatica,2001,37 (7):1029-1039.
[11]罗小元,武晓晶,华长春,等.基于观测器的非线性系统执行器死区故障的自适应跟踪控制[J].系统工程与电子技术,2009,31 (7):1701-1704.LUO XIAOYUAN,WU XIAOJING,HUA CHANGCHUN,et al.Adaptive tracking of nonlinear systems with actuator dead-zone fault based on observer[J].Systems Engineering and Electronics,2009,31 (7):1701-1704.
[12]HU QINGLEI,MA GUANGFU.Maneuvers and vibration suppression of flexible spacecraft with input nonlinearities[J].Aircraft Engineering and Aerospace Technology,2005,77 (5):388-400.
