Matlab在通信原理课程教学中的应用

孙钢灿

(郑州大学 信息工程学院，河南 郑州 450001)

1 通信原理课程特点及教学需求

通信原理课程是通信工程、电子信息工程及相关专业本科生的一门重要的专业基础课程,它在通信工程专业的课程体系结构中起着非常重要的作用,是学习后续课程的基础.本课程的理论性和实践性都很强,涉及的知识面也很广泛,难以掌握和融会贯通，因此,如何有效地提高通信原理课程的教学质量、使学生具有较强的主动获取知识和独立解决问题的能力是一项重要的工作.

通信原理课程的理论学习往往有大量复杂的数学推导,学生不会将理论知识运用于实践;同时,由于本课程的内容偏重理论,容易造成学生在学习过程中理论和实践相分离,学习效果不好.Matlab软件作为一套功能强大的科学计算工具,已成为世界上越来越多的科研和工程技术人员进行科学研究与计算的必备工具.利用Matlab强大的计算仿真和方便易用的图形绘制功能,将抽象的理论以易于理解的形式展示给学生,能达到良好的教学效果.本文通过数字调制系统中2PSK的性能分析教学,将这方面的教学经验作为案例加以介绍.

2 Matlab 软件[1-4]

Matlab由MATrix和LABoratory两词的前3个字母组合而成.20 世纪70 年代后期,时任美国新墨西哥大学计算机科学系主任的Cleve Moler教授为了减轻学生的编程负担,为学生设计了一组调用LINPACK和EISPACK库程序的通俗易用的接口,即用FORTRAN 编写的萌芽状态的Matlab.经几年的校际流传,在Little的推动下,由Little，Moler和Steve Bangert合作, 于1984年成立了MathWorks公司,把Matlab正式推向了市场.从这时起,Matlab 的内核采用C语言编写,除了原有的数值计算能力外,还新增了数据图视功能.

Matlab的语句简单明了，更符合人们平常的思维习惯，它具有良好的数据可视化功能，能将数字结果的形式表现出来，让人一目了然，已被广泛应用于数学计算和分析、自动控制、人工智能、模糊逻辑、通信系统分析与仿真、图形图像处理、金融系统、数理统计等领域.

3 数字通信系统蒙特卡洛仿真原理

蒙特卡洛仿真是指那些利用蒙特卡洛方法估计系统参数如误比特率(BER)的方法，它利用感兴趣事件出现的频率来估计其发生的概率.下面首先介绍数字通信系统性能的蒙特卡洛仿真，然后比较2PSK系统的误码率仿真结果和通信原理教科书给出的误码率理论计算结果，在此基础上加深学生对2PSK系统的误码率性能分析相关理论的理解.

通信系统的低通等效(MASK、MPSK、MFSK)见图1.调制器的输出端假设的带通信号可以表示为

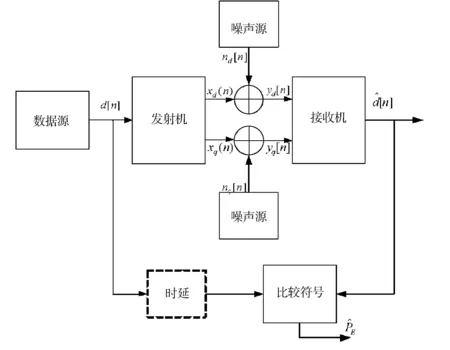
图1 简单通信系统仿真模型Fig.1 Simulation model for simple communication system

x(t，n)=Accos[2πfct+kmd[n]+θ]，

(1)

其中，Ac表示载波幅值，km是跟调制相关的常数，d[n]是第n个数据符号，θ是参考相位，因此，欧拉公式x(t，n)的复包络为

x(n)=Acexp{kmd[n]+θ}，

(2)

假设其中参考相位θ=0，所以图1中有

xd(n)=Accos(kmd[n])，

(3)

和

xq(n)=Acsin(kmd[n]) .

(4)

为了确定画出以Eb/N0为函数的误码率，保持Eb恒定，并让噪声功率在感兴趣的范围内递增，要求对图1中的噪声发生器输出端的噪声功率进行校准.由文献[5]可知，噪声方差和噪声功率谱密度(PSD)的关系为

(5)

其中，fs为采样频率，信噪比SNR定义为Eb/N0，因此有

(6)

如果能量Eb和采样频率fs都归于1，则有

(7)

上式用于确定后面仿真中的噪声标准差.

为了产生二进制PSK信号的同相和正交信号空间分量，在式(3)和式(4)中令Ac=1和km=π，由此得到

(8)

同时，xq(n)=sin(πd[n])=0，这样就给出了二进制PSK信号的空间表示，如图2所示.图2中，φ1是信号空间的基函数.由于信号空间是一维的(1个基函数产生)，在仿真中只要产生信号和噪声的直接分量，图1所示的正交分量就可以丢弃掉.

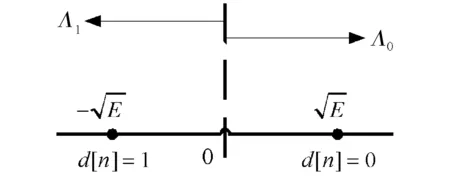
图2 二进制PSK的信号空间表示Fig.2 Signal space representation of binary PSK

(9)

由通信原理[7]可知，采用相干解调方法时，2PSK系统总误码率为

(10)

其中，r为信噪比，另一种经常用来表示误码率的函数是Q函数，由通信原理知

(11)

(12)

因此,误码率的理论值还可以表示为

(13)

结合上面给出的蒙特卡洛仿真结果和通信原理理论给出的误码率结果，采用Matlab的M语言给出2PSK系统的误码率仿真实验程序如下：

snrdB_min = -3; snrdB_max = 8; % SNR (in dB) limits

snrdB = snrdB_min:1:snrdB_max;

Nsymbols = input('Enter number of symbols > ');

snr = 10.^(snrdB/10); % convert from dB

h = waitbar(0,'SNR Iteration');

len_snr = length(snrdB);

for j=1:len_snr % increment SNR

waitbar(j/len_snr)

sigma = sqrt(1/(2*snr(j))); % noise standard deviation

error_count = 0;

for k=1:Nsymbols % simulation loop begins

d = round(rand(1)); % data

x_d = 2*d - 1; % transmitter output

n_d = sigma*randn(1); % noise

y_d = x_d + n_d; % receiver input

if y_d > 0 % test condition

d_est = 1; % conditional data estimate

else

d_est = 0; % conditional data estimate

end

if (d_est = d)

error_count = error_count + 1; % error counter

end

end % simulation loop ends

errors(j) = error_count; % store error count for plot

end

close(h)

ber_sim = errors/Nsymbols; % BER estimate

ber_theor = q(sqrt(2*snr)); % theoretical BER

semilogy(snrdB,ber_theor,snrdB,ber_sim,'o')

axis([snrdB_min snrdB_max 0.0001 1])

xlabel('SNR in dB')

ylabel('BER')

legend('Theoretical','Simulation' )

2PSK系统的误码率仿真结果由图3给出.图3中，横轴为SNR，纵轴为误比特率BER(2PSK中误码率和误比特率相等)，两条曲线分别代表蒙特卡洛仿真结果和通信原理教材给出的理论计算结果.对于每一个SNR值，发送10 000个符号，从图中看出仿真结果和理论值基本一致.但是，当SNR增加时，BER估计器的可靠性会变差，这是由于差错发生次数减少的缘故.这表明，仿真次数的选择应该与SNR有关，或者连续运行仿真程序，直到每个SNR值都记录到相同数目的差错为止.

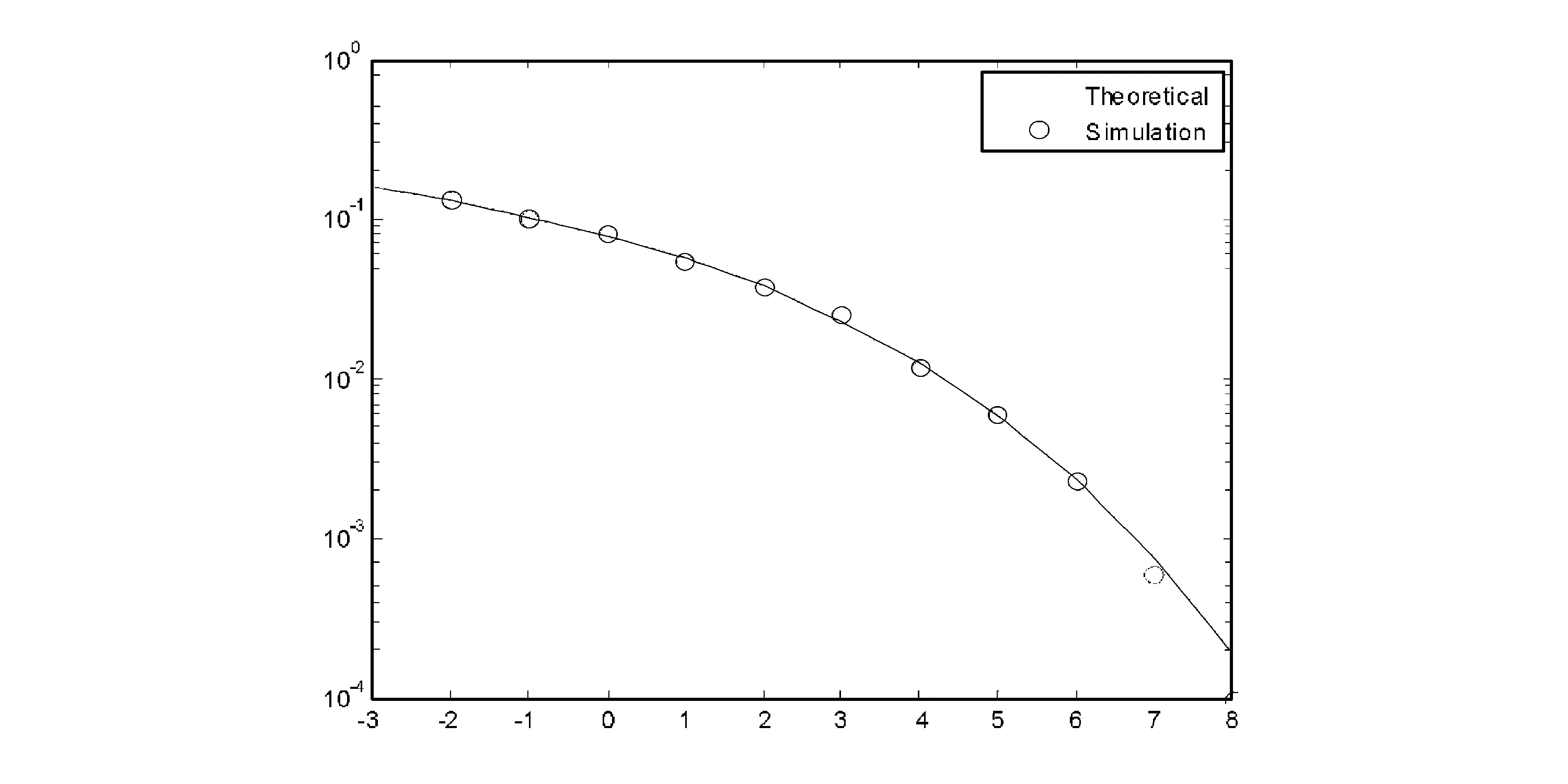
图3 二进制相移键控误比特率仿真结果Fig.3 The simulation results of Binary phase-shift keying

4 结束语

该案例给出了用Matlab工具学习通信原理课程的方法，这种方法可以使通信原理的抽象理论更易于学生理解.利用Matlab语言易于使用、后处理功能强大的优点，在通信原理课程的教学中，还可以帮助其他章节的授课，如随机信号和数字基带信号的谱特性、模拟信号的数字传输、数字信号的最佳接收等.将通信原理的主要内容以实例的形式展现, 可以将抽象的概念具体化,达到加深理解、强化记忆的效果, 既能激发学生学习的积极性, 也能提高教学质量, 具有实际意义.

参考文献：

[1] 程铃,徐冬冬.Matlab仿真在通信原理教学中的应用[J].实验室研究与探索,2010，29(2): 117-119.

[2] 刘宏波.Matlab在通信原理课程教学中的应用实例[J].实验技术与管理,2009，26(10): 87-89.

[3] 孙爱晶,刘毓.基于软件仿真的通信原理实验教程[J].实验室研究与探索,2010，29(1): 135-137.

[4] 周晓兰,张杰.Matlab在通信系统仿真中的应用[J].计算机技术与发展,2006，16(9): 166-168.

[5] Tranter W H.Principles of Communication System Simulation with Wireless Aplications[M].New Jersey: Perntice Hall，2003.

[6] Ziemer R E，Tranter W H.Principles of Communications: Systems, Modulations and Noise[M].New York: Wiley，2002.

[7] 樊昌信,曹丽娜.通信原理[M].北京: 国防工业出版社，2008.