连续刚构桥施工阶段稳定性敏感因素分析
2011-11-24康玉强龚尚龙吴海军
康玉强,龚尚龙,吴海军,王 豪
(重庆交通大学 土木建筑学院 ,重庆 400074)
随着我国交通运输事业的发展及西部大开发战略的进一步深入,在高原沟壑修建的桥梁也越来越多.连续刚构桥集高墩大跨、造价低、施工方法灵活等优点于一身,与其他桥型相比竞争力较强,在山区路段修建较多.为了能有效地减少上部结构的内力和温度、混凝土收缩徐变以及地震的影响,要求顺桥向墩的抗推刚度小,加之高强度材料和先进施工方法的不断出现,预应力混凝土连续刚构桥开始向薄壁、高墩和大跨径发展,这就使其稳定问题日渐突出.为了确保大跨高墩连续刚构桥的安全使用,对其进行稳定分析非常必要.
1 基本理论和方法
1.1 连续刚构施工阶段稳定分析现状
由于采用薄壁高墩,连续刚构桥的刚度逐渐减少,但又比柔性结构的斜拉桥、悬索桥的刚度大得多.后者的抗风稳定性问题主要通过风洞实验解决,理论计算在一定程度上是辅助手段.试验研究得到的结果较为准确,但耗费时间长、费用高.一般来说,有关连续刚构桥动力稳定的研究很少,大都在可以接受的安全储备的前提下,简化成等效静力计算[1-2].由于影响桥梁施工阶段稳定性的因素众多,难以通过简单的推导得到各要素对稳定性的影响程度,所以本文将通过实桥计算来比较分析施工阶段各要素对连续刚构桥梁稳定性的影响规律及趋势.
1.2 桥梁稳定性分析的基本方法和作用
1.2.1 第一类稳定
根据最小势能原理,可以推出第一类稳定问题的有限元平衡方程[3]为:
([KD]+[Dσ]){δ}={F},
(1)
式中,[KD]为结构弹性刚度矩阵,与外荷载无关,取决于结构的几何尺寸和材料的物理性能;[Kσ]为结构的几何刚度矩阵,与荷载大小有关;{δ}为节点位移向量;{F}为节点荷载向量.
设{F}增加λ倍,则杆内力和几何刚度矩阵相应增加λ倍,因而可以写出下式:
([KD]+λ[Kσ]){δ}=λ{F},
(2)
如果λ足够大,使得结构达到随遇平衡状态,即当{δ}变为{δ}+{Δδ},上列平衡方程也能满足,则:
([KD]+λ[Kσ])({δ}+{Δδ})=λ{F},
(3)
同时满足(1)、(2)两式的条件是:
([KD]+λ[Kσ])(Δδ)=0,
(4)
这就是要计算稳定安全系数的特征方程,若结构有n个自由度,则方程亦为n阶方程,在理论上存在n个特征对,特征值即为安全系数,特征向量即为失稳模态.在实际工程中,只有最小正的特征值λcr才有意义,为最小安全系数,此时对应的失稳临界荷载为λcr{F}.当荷载达到λcr{F}后,结构的总刚度([KD]+λ[Kσ])为零,有无穷多个解,结构失去抵抗能力,变形无限大.
1.2.2 第二类稳定
第二类稳定,极值点失稳,就是不断计入结构几何非线性和材料非线性的刚度方程,寻找结构极限荷载的过程.引入结构几何非线性和材料非线性,平衡方程的有限元列式为:
(t[Kep]+t[Kσ]){Δδ}=t[K]T{Δδ}={ΔF},
(5)
式中,t[Kep]为t时刻弹塑性刚度矩阵;t[Kσ]为结构t时刻的几何刚度矩阵;t[K]T为切线刚度矩阵;{Δδ}和{ΔF}分别为位移增量和荷载增量.
弹塑性刚度矩阵可由下式求得:
(6)
式中,[Dep]为材料弹塑性矩阵;[B]为应变矩阵;v表示整个体积域.
设屈服函数为:
F(σij,K)=0,
(7)
式中,σij为应力状态;K为硬化函数.
在增量理论中,材料达到屈服以后的应力增量与应变增量关系及其相应的弹塑性矩阵可以写为:
{dσ}={Dep}{dε},
(8)
(9)
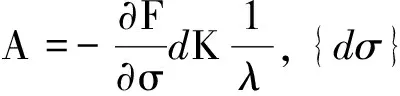
在连续刚构桥的稳定性分析中,经常采用特征值分析和非线性分析相结合的方式.特征值分析的主要目的是估计各阶临界荷载的上限,并确定相应的失稳模态.通常,确定最小的特征值及模态作为非线性分析的依据.由于连续刚构的墩高,必须同时考虑几何非线性和材料非线性的影响,其相应的初始缺陷由一阶模态确定,得到的临界荷载小于特征值分析的结果.根据已有分析结果,只计入材料非线性的结果略大于计入双非线性的结果,两者相差约5%,都为特征值的50%左右,故特征值分析能判断出屈曲荷载范围,能定性地判断结构的刚度是否合理,在结构设计的初期具有相当重要的理论和现实意义.
1.3 稳定分析单元类型的选择
在施工阶段,稳定分析一般不考虑预应力的作用,故存在以下3种单元组合方式供选择:①主梁、墩均采用梁单元,这种方法简单容易实现,整体稳定分析时适用;②主梁、墩均采用壳单元,这种组合能考虑局部板件的屈曲,如面外腹板失稳;③主梁采用梁单元,墩采用实体单元,此时可以在墩身中加入钢筋,并耦合钢筋与混凝土的自由度,实现变形协调,这种方法较为精确,尤其是能很好地分析墩在失稳过程中的结构行为.以上3种单元组合方式可用作特征值分析和非线性分析.在做非线性稳定分析时,梁、板单元一般采用双线性或多线性弹簧单元考虑塑性,实体单元一般采用Willam&Warnke破坏准则、Von Mises屈服准则及关联流动法则考虑塑性.很明显,后一种方法更为精确,但计算工作量大、成本高.
2 工程概况
东峪特大桥位于张石公路化稍营至蔚县(张保界)段高速公路 LK60+968.00(左线)及RK61+048(右线)处,横跨东峪河谷.本桥为跨径组成88 m+160 m+88 m三跨连续刚构,最大墩高56 m,采用施工方法为挂篮悬臂施工.该桥地处山口位置,地形恶劣,常年有大风,故在施工阶段应考虑风载引起的稳定问题.
3 有限元模型的建立及分析
3.1 模型及边界
由于连续刚构桥失稳多为墩的失稳,故计算时把墩高作为变化参数,分别将墩高增加1#墩高的50%(28 m)和100%(56 m),考查在荷载作用下墩高变化对稳定的影响.在施工阶段考虑预应力超张对稳定的影响.对此桥做特征值分析,分析和比较墩高、风力、挂篮、不对称施工荷载等因素对桥梁稳定的影响,为设计、施工提供指导.
3.2 荷载计算
3.2.1 风荷载计算
本桥风载计算按照JTGD 60—2004《公路桥涵设计通用规范》执行,参照推荐性行业标准JTG/TD 60-01—2004《公路桥梁抗风设计规范》.简化为静力计算,将风载等效施加到节点上[4-5].
(1)横桥向风荷载假定水平地垂直作用于桥梁各部分迎风面积得形心上标准值按规计算:
Fwh=k0k1k3WdAwh,
(5)
其中,k0为设计风速重现期换算系数,本桥为特大桥,取k0=1.0;k1为风载阻力系数,主梁的k1按(6)式计算:
(6)
式中,B为桥梁宽度,H为梁高;k3为地形、地理条件系数,本桥处在山间谷地,取k3=0.85;Wd为设计基准风压,随高度变化;Awh为迎风面积,在成桥阶段计入护栏的迎风面积.
(2)桥墩上顺桥向的风荷载标准值可按横桥向风压的70%乘以桥墩迎风面积计算:
① 主梁上顺桥向单位长度的风荷载取其横桥向风荷载的0.25倍;
传统摄影在摄影发展过程中凝结着中国乃至世界众多传统文化艺术家的智慧结晶,习近平在文艺工作座谈会上的讲话中指出,建设中国特色社会主义文化强国,需要将传统文化艺术发扬光大。如蓝晒摄影作品,作为传统摄影拍摄手法,在数码摄影拍摄手法的基础上,运用传统摄影的拍摄工具,拍摄具有现代摄影气息的传统摄影作品,以传统摄影的手法表现当代社会的特征,表现富有当代文化艺术气息的文化背景,创作与当今时代相呼应的优秀摄影作品。
② 成桥阶段的迎风面积还应计入护栏的影响;
③ 施工阶段应考虑不对称横向风作用在主梁上对墩的扭转作用.
3.2.2 施工阶段其他荷载
施工阶段结构荷载不断变化,基于安全考虑选取最大悬臂状态分析.期间可能承受的荷载有以下几种:
(1)自重,按设计图纸确定;
(2)预应力,按设计图纸确定;
(3)挂篮,按设计取值,1 100 kN;
(4)不均匀自重,由于施工误差一侧取1.05倍自重,另一侧取0.95倍自重;
(5)挂篮跌落,并考虑2倍的冲击系数;
(6)不平衡施工荷载;
(7)施工单位在梁体上堆放的一些工具材料,计算时一端悬臂作用有8.5 kN/m的均布荷载,并在其端头有200 kN的集中力,另一侧悬臂空载.
以上各种荷载按最不利进行组合,一共分16种组合计算.
工况1:自重;
工况2~4:自重+不均匀自重+(1、1.5、2)倍挂篮;
工况5:自重+不均匀自重+主梁纵横向风;
工况6:自重+不均匀自重+墩纵横向风;
工况7:自重+不均匀自重+主梁、墩纵横向风;
工况8:自重+不均匀自重+墩纵横向风+主梁纵向风+主梁横向不对称风;
工况9:自重+不均匀自重+主梁、墩纵横向风+不平衡施工荷载;
工况10:自重+不均匀自重+主梁、墩纵横向风+不平衡施工荷载+挂篮跌落;
工况11~16分别为工况5~10的风载放大2倍,其他荷载不变.
3.3 计算工况及结果
从失稳模态(见图1)可以看出,该桥施工阶段第一阶失稳为面内失稳,表现为纵倾,面外刚度大于面内刚度,桥梁的稳定性取决于墩的刚度.

图1 施工阶段失稳模态 Fig.1 Bulking mode during construction
稳定系数随荷载组合变化图(见图2)表明,在施工阶段作用于桥梁的荷载越多,稳定系数越小.同时,从工况8、9和工况14、15之间的突变可以看出,不平衡施工荷载作用下稳定系数突然减少.据此,在连续刚构的施工过程中,应严格控制混凝土浇筑方量,在主梁上堆放的施工设备及材料应注意做到两侧平衡.图中2条走势一致、偏差比不大,说明静风荷载的变化对稳定的影响在各因数中占的比例较小.
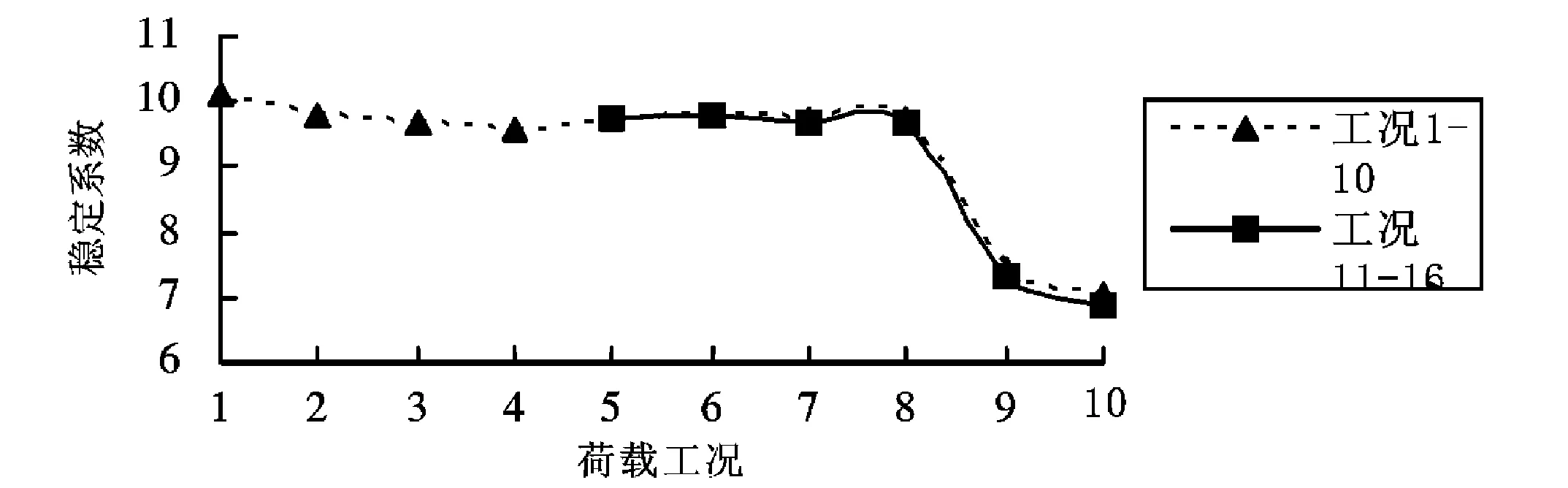
图2 稳定系数随荷载组合变化图Fig.2 Stability factor vs the load combination
从稳定系数随墩高变化图(见图3)可以看出,随着荷载的增加,稳定系数逐渐减少,总体呈现相似的变化规律;在相同的荷载组合条件下,稳定系数对墩高的变化更为敏感,稳定系数随墩高的变化率变小,说明设计墩高处于一个较合理的高度.

图3 稳定系数随墩高变化Fig.3 Stability factor vs the height of pier
稳定系数随挂篮重量变化图(见图4)表明,挂篮重量增加50%和100%对稳定的影响不是很明显,与主梁的自重相比挂篮很轻,其变化不足以影响整体的稳定性,只是其引起的静挠度在施工控制时应加以考虑.
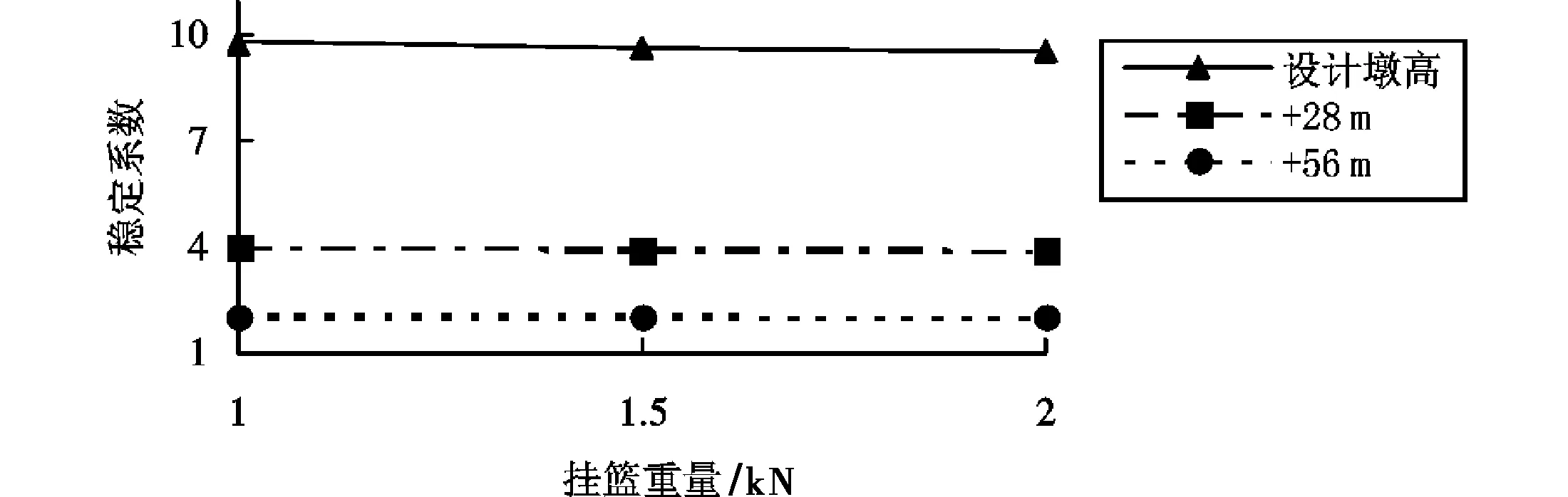
图4 稳定系数随挂篮重量变化Fig.4 Stability factor vs the weight of traveller
4 结语
通过对东峪特大桥在施工和成桥阶段进行特征值屈曲分析,可以初步得出如下结论:(1)在施工期间,结构的最小稳定系数为7.044,稳定系数与同类桥相近,能保证施工期间安全;(2)在施工时,稳定系数对挂篮重量变化不是很敏感,而风载单独作用对稳定系数的影响较小,原因是风载引起的墩的轴力小;(3)不均衡自重和挂篮跌落是影响稳定的主要因素,在施工时应着重注意控制挂篮的锚固及混凝土浇筑的进度.
同时,在连续刚构的稳定分析中仍存在以下问题:(1)收缩徐变的影响在特征值分析及非线性分析中是没有考虑的;(2)不同成桥方式的成桥内力不同,故在做成桥阶段稳定性分析时,引入施工阶段的累积内力(应力)是值得研究的.
参考文献:
[1] 程进,肖汝诚,项海帆.大跨径桥梁静风稳定性分析方法的探讨与改进[J].中国公路学报,2001,14(2):30-32.
[2] 李萍,廖萍,龙晓鸿,等.薄壁高墩大跨度连续刚构桥的非线性稳定分析[J].工程力学,2006,23(5):119-124.
[3] 李国豪.桥梁结构稳定与振动[M].北京:中国铁道出版社,1996.
[4] JTGD 60-2004.公路桥涵设计通用规范[S].2004.
[5] JTG/TD 60-01-2004.公路桥梁抗风设计规范[S].2004.
[6] 王解军,梁锦锋.风载作用下高墩连续刚构桥的非线性稳定分析[J].中南林业科技大学学报,2008,28(2):74-79.
[7] Yaua J D,Yangb Y B. Geometrically nonlinear analysis of planar circular arches based on rigid element concept—a structural approach[J].Engineering Structures, 2008,30(1):955-964.
[8] Hamid R,Valipour,Stephen J,et al. Nonlinear reinforced concrete frame element with torsion[J].Engineering Structures,2010,32(1):988-100.
