一种非线性不确定系统的鲁棒H∞滤波方法研究*

乔国栋，黎 康，曾海波

（1.北京控制工程研究所，北京 100190；

2.空间智能控制技术重点实验室，北京100190）

一种非线性不确定系统的鲁棒H∞滤波方法研究*

乔国栋1，2，黎 康1，2，曾海波1，2

（1.北京控制工程研究所，北京 100190；

2.空间智能控制技术重点实验室，北京100190）

考虑EKF滤波方法的线性化过程对估计误差的影响，提出一种非线性不确定系统的鲁棒H∞滤波方法.基于 H∞理论，该算法将滤波模型和观测模型在线性化过程中所产生的误差作为系统的不确定部分，力求此误差对导航精度的影响最小，并且利用李亚普诺夫方法证明了该滤波算法的稳定性.利用所提算法对月球环绕段自主导航系统进行滤波估计，仿真结果证实了算法的有效性.

李亚普诺夫稳定性；非线性不确定系统；鲁棒H∞滤波；月球探测

自主导航系统都是精密的，但其工作的环境容易受到各种外界环境的干扰，另外，其本身也存在着传感器误差，这些因素都会影响导航的精度.为了在已有硬件基础上提高导航精度，必须采取强有效的滤波方法.目前应用最广泛的是扩展卡尔曼滤波［1］，这是一种非线性滤波方法，该算法在线性化过程中忽略高阶项，必然会降低导航精度，且当模型受到干扰发生变化时，EKF滤波算法往往会使系统发散［2］.

本文提出一种非线性不确定系统的鲁棒H∞滤波方法，该算法是基于H∞理论［3］设计的，将滤波模型和观测模型在线性化过程中所产生的误差作为系统的不确定部分，力求其对导航精度的影响最小，通过李亚普诺夫方法证明了该鲁棒H∞滤波算法的稳定性，利用所提算对月球环绕段自主导航系统进行滤波估计，证实了所提算法的精度优于传统的EKF算法.

1 鲁棒H∞滤波器的结构

考虑非线性不确定系统：

式中，x（t）表示状态变量；y（t）表示测量输出；w（t）为系统的模型误差，即不确定项；为测量噪声，其统计特性已知，即

对于非线性不确定系统（1），设计鲁棒H∞滤波器形式为

式中，P（t）是黎卡提方程的解，R为系统的测量方差阵.定义系统的估计误差为ζ=x（t）-（t），则估计误差的动力学方程为

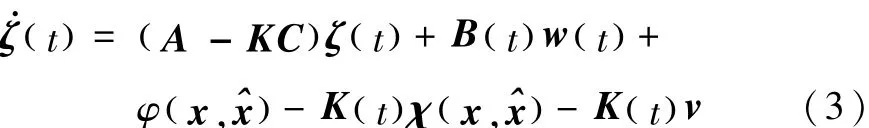
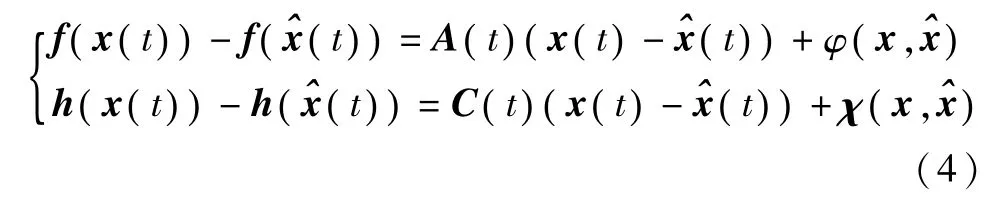
式中，γ为H∞控制中的衰减因子，Q为有界的对称正定矩阵.

2 鲁棒滤波器稳定性证明

为了保证鲁棒H∞滤波器的稳定性，需作如下

假设：

假设1.P矩阵为对称有界阵，即

式中，p1，p2均为正实数.

假设2.模型误差 w和测量噪声 v，分别满足 w，v∈L2，w，v∈L∞.

假设3.对于式（5）中的L，定义LTL是有界的，即

式中，l1，l2为正实数.

假设4.观测矩阵C（t）是有界的

式中，c2为一正实数.

假设 5.存在正实数 κφ，εφ与 κχ，εχ，能够保证非线性残差项满足

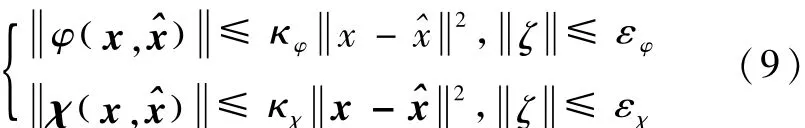
引理 1［3].若假设 4、5满足，则存在常数 ε=对于一切满足条件以及的 ζ，均满足

对于非线性鲁棒 H∞滤波器（2）和（3），选取李亚谱诺夫函数

式中，P（t）为黎卡提微分方程（5）的解，由假设1可知：

由式（12）可以看出，V（t）为正定有界函数.对式（11）计算微分，得

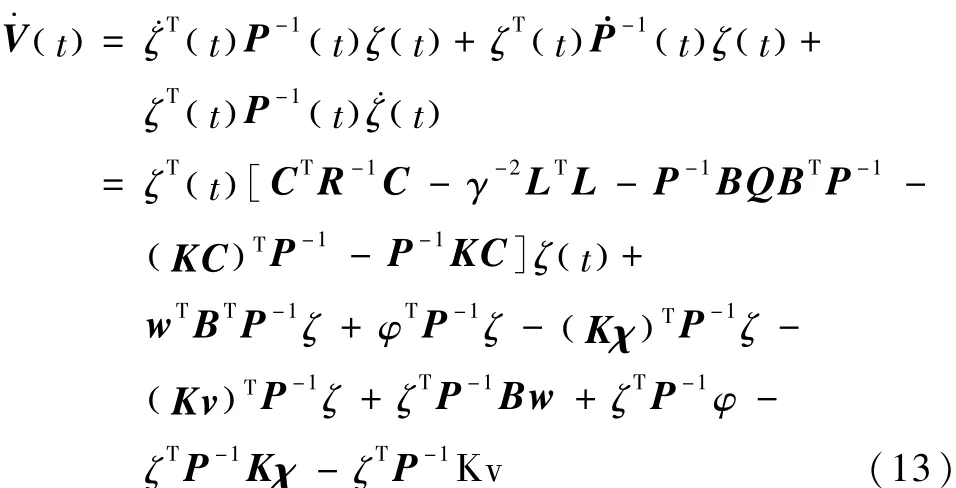
式中，P-1可由黎卡提微分方程（5）计算，

由此可得

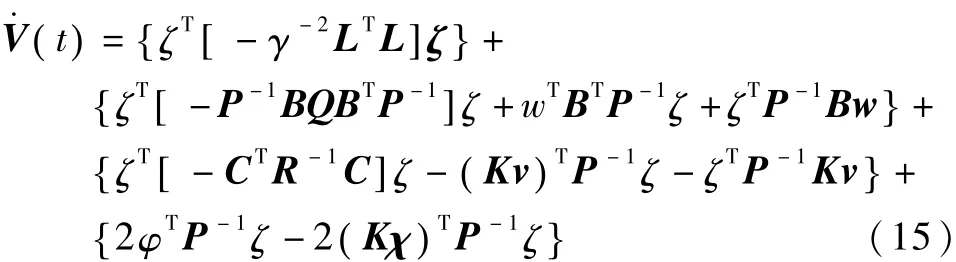
式（15）中的第二项可改写为

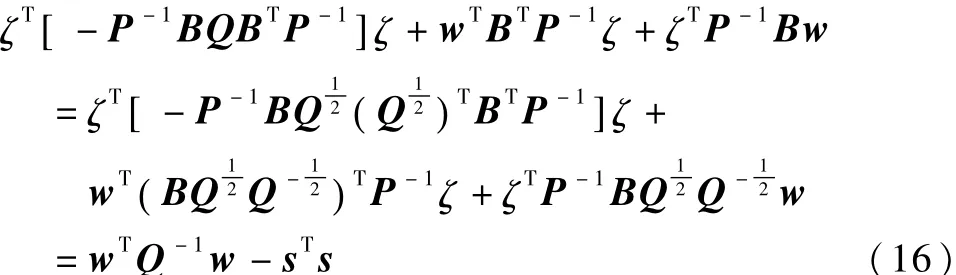
将式（16）和式（17）代入式（15），得

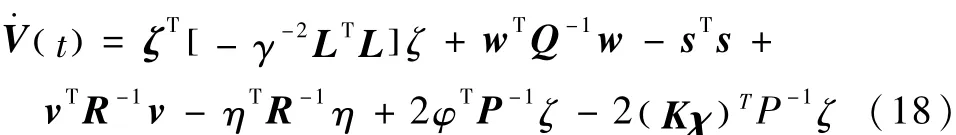
由引理1，可得

若估计误差ζ≤ ε2，则

式（21）中的残差项wTQ-1w+vTR-1v由假设2得

式中，dw，dv分别为w和v的上界，μ，r分别为Q，R阵的下界，对式（21）两边进行积分，得

考虑到V（t）=ζT（t） P-1（t）ζ（t），且

ζT其中 p2a为 P（t）矩阵的上界，因此，

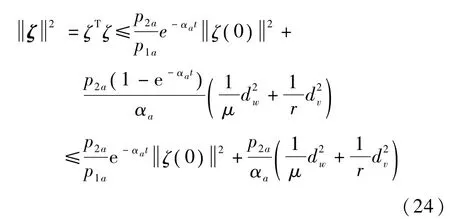
式中，p1a为P（t）矩阵的下界，随着时间的增加，式（24）中的第一项逐渐趋于零，所以，误差的稳态值为

给出所提鲁棒H∞滤波器的代价函数，由假设3及式（20）可知：

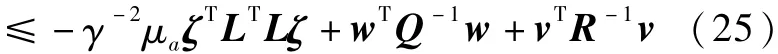
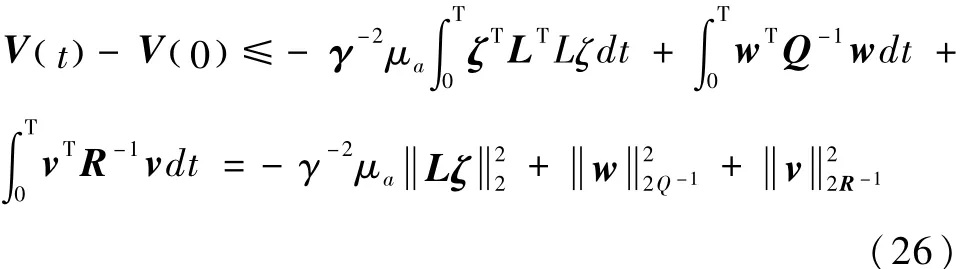
式中定义：

定义鲁棒H∞滤波器的代价函数为

3 鲁棒H∞滤波器设计方法

前面已经给出鲁棒H∞滤波器的构型来进行稳定性分析，本节主要给出鲁棒H∞滤波器的设计步.

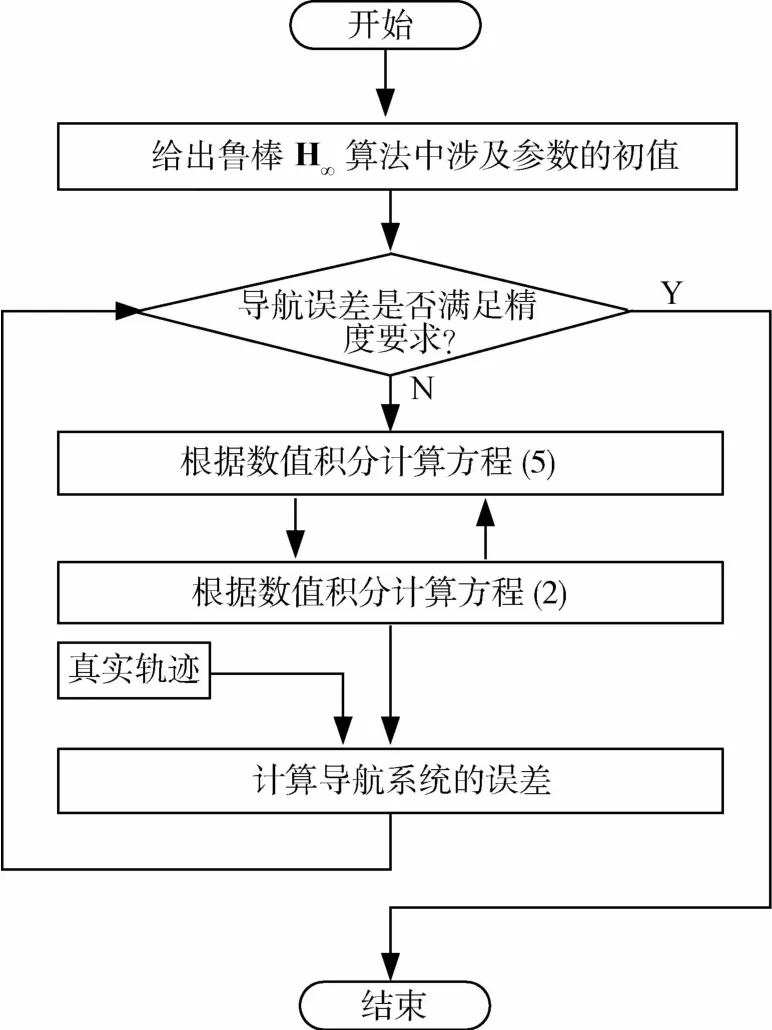
图1 鲁棒H∞滤波器的设计步骤

由图1可知，本文所提的鲁棒 H∞滤波算法将传统的EKF算法中的测量更新步骤分解到方程（2）与方程（5）中，仅仅需要计算2个微分方程，就能够解算导航系统的状态变量，操作方便.

4 月球探测环绕段仿真

为了验证所提鲁棒 H∞滤波算法的有效性，以月球探测环绕段［4-5］自主导航系统为例，分别利用所提算法与EKF算法对导航系统进行滤波估计，然后分析两者的计算结果.

4.1 仿真条件

导航坐标系：月心J2000惯性系.起始时间：2007.7.1，12：00.结束时间：2007.7.2，12：00.轨道初始根数：

（1）半长轴：1938km；

（2）离心率：0.001；

（3）轨道倾角：89.5。；

（4）近月点幅角：45。；

（5）升交点赤经：45。；

（6）平近点角：0。.

真实模型：由STK产生，主要考虑的摄动加速度包括月球非球形引力摄动，地球引力摄动，太阳引力摄动，月球固体潮摄动，月球物理天平动.

滤波模型：仅考虑月心引力.

测量频率：30s.

观测模型：月心矢量及视半径.

测量误差：0.06。（1σ）.

滤波估计状态变量：探测器的位置和速度.

滤波算法：鲁棒H∞滤波算法.

滤波算法中所用参数选取：

矩阵 B=I6×6，I表示单位矩阵.

矩阵 L=I6×6.

矩阵 P=10-8I6×6.

加权矩阵 Q=10-3I6×6.

4.2 滤波模型

导航滤波方程仅考虑月球重力场中心引力，其它摄动项归入动力学模型误差［6］.导航滤波器的状态包括探测器在月心赤道惯性系中的位置矢量r=［x y z］T和速度矢量 v=［vxvyvz］T.轨道动力学方程可改写为如下的状态方程，

式中x为状态矢量，w为动力学模型误差，可作为模型噪声，

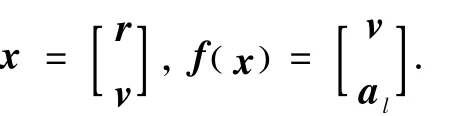
在扩展卡尔曼滤波（EKF）算法中要用到状态转移阵，可如下计算：

月心引力加速度al对位置矢量r和速度矢量v的偏导数分别为

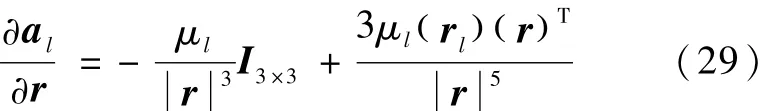
式中，rl表示月球星历.系统的状态转移矩阵 Φ在忽略高阶项的情况下，可采用 Taylor展式计算得

式中，A表示偏微分矩阵；Δt表示仿真步长.

4.3 观测模型

以月心矢量ul作为观测量，则测量方程为

式中，r和rl分别代表探测器和月球的位置矢量；以月球视半径θ作为观测量，则观测方程为

式中，Rm代表月球半径.

4.4 仿真结果

图2与图3分别给出了鲁棒H∞滤波与传统的EKF算法计算的位置误差与速度误差.

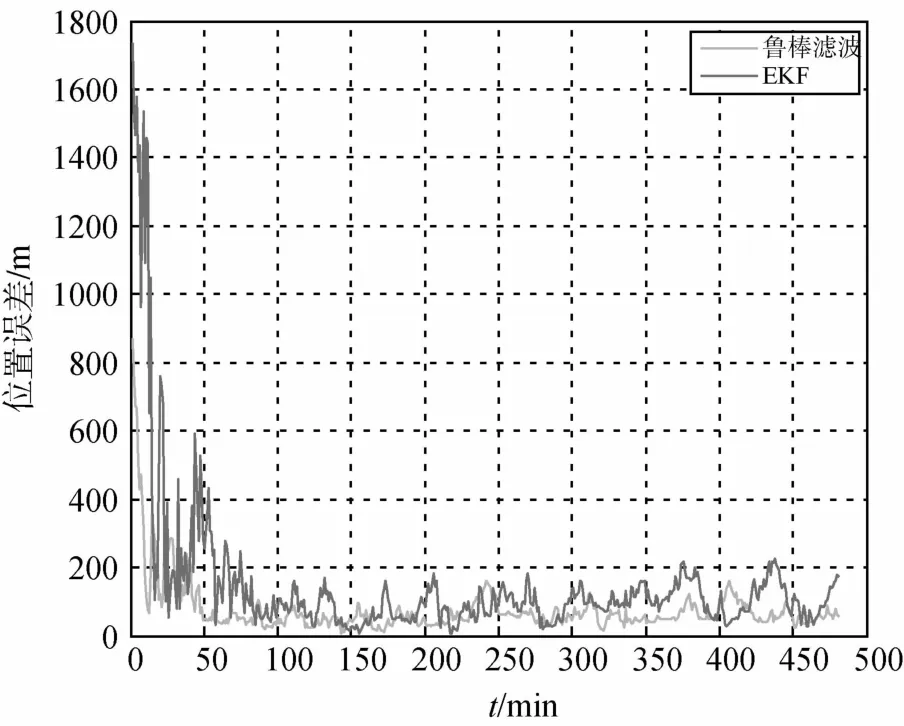
图2 鲁棒H∞滤波与EKF位置误差比较

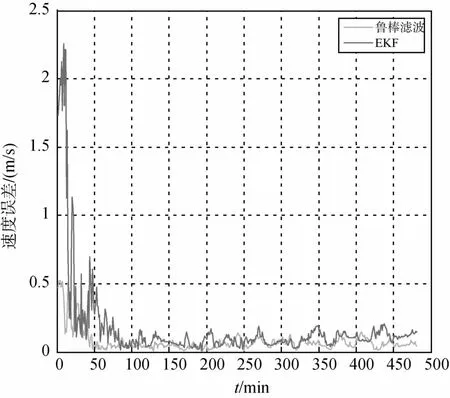
图3 鲁棒H∞滤波与EKF速度误差比较

从图中可以看出，在相同初始条件的前提下，鲁棒H∞的滤波算法的计算结果明显优于传统的EKF滤波算法.

5 结 论

本文提出一种非线性不确定系统的鲁棒H∞滤波方法，该算法结构简单，仅需要解算两个微分方程（式（2）、（5）），就可将状态变量准确的估算出来，同时所提的鲁棒H∞滤波算法将模型在线性化过程中所产生的误差作为系统的不确定部分，力求将此误差对导航精度的影响降至最小，通过对月球环绕段自主导航系统的仿真研究，证实了所提算法的精度优于传统的EKF算法.

［1］ 秦永元，张洪钺，汪叔华.卡尔曼滤波与组合导航原理［M］.西安：西北工业大学出版社，2004

［2］ Xiong K，Liu L D，Liu Y W.Nonlinear robust filter design for satellite attitude determ ination［J］ IET Control Theoryamp;Applications， 2010，4（7）：1222-1234

［3］ Rief K S.An EKF-based nonlinear observer with a prescribed degree of stability［J］.Automatica， 1998，34（9）：1119-1123

［4］ 宗红，王淑一，王大轶.嫦娥一号卫星的地月转移变轨控制［J］.空间控制技术与应用，2008，34（1）：44-50

［5］ 黄欣，卢欣.嫦娥一号卫星紫外月球敏感器［J］.空间控制技术与应用，2008，34（1）：51-55

［6］ 刘林，王歆.月球探测器轨道力学［M］.北京：国防工业出版社，2006

Robust H∞Filter A lgorithm for Non linear Uncertain System

QIAO Guodong1，2，LIKang1，2，ZENG Haibao1，2
（1.Beijing Institute of Control Engineering， Beijing 100190；2.Science and Technology on Space Intelligent Control Laboratory， Beijing 100190， China）

In light of the effect of linearization on estimation error in EKF filter，a kind of robust H∞filter algorithm for nonlinear uncertain system is proposed.Based on H∞theory， the proposed algorithm is designed.The linearization errors of filter model and measure model are defined as uncertain parts of the system；the robust H∞filter algorithm could m inim ize the effect of uncertain parts on navigation acccuracy.By using Lyapunov method，the stability of proposed algorithm is proven.Both robust H∞filter algorithm and EKF algorithm are utilized to estimate states of the autonomous navigation system in the lunar-rounding phase，the simulation results validate effectiveness of the robust H∞filter algorithm.

Lyapunov stability； nonlinear uncertain system；robust H∞filter；lunar exp loration

V448

A

1674-1579（2011）04-0045-04

10.3969/j.issn.1674-1579.2011.04.009

*国防基础科研项目（A0320080019）.

2011-05-28

乔国栋（1980—），男，山西人，工程师，研究方向为制导、导航与控制（e-mail：qiaoguodong@bice.org.cn）.