几乎处处收敛、近一致收敛和依测度收敛之间的等价条件研究

续小磊 (宁夏大学数学计算机学院,宁夏 银川 750021)

续晓欣 (中北大学理学院数学系，山西 太原 030051)

几乎处处收敛、近一致收敛和依测度收敛之间的等价条件研究

续小磊 (宁夏大学数学计算机学院,宁夏 银川 750021)

续晓欣 (中北大学理学院数学系，山西 太原 030051)

研究了函数列的近一致收敛、几乎处处收敛和依测度收敛之间的关系，在此基础上给出了它们之间彼此等价的充分必要条件。

测度；可测集；可测函数列；几乎处处收敛；近一致收敛；依测度收敛

可测函数序列的收敛性有很多种，如几乎处处收敛、依测度收敛、依概率收敛、完全收敛、一致收敛、几乎一致收敛、近一致收敛、平均收敛、强收敛和弱收敛等。如此多收敛之间的强弱关系引起了许多测度论学者们的关注[1-6]。其中，几个经典定理，如Egoroff (逆)定理、Lebesgue定理、Riesz定理在测度有限的前提下对几乎处处收敛、近一致收敛和依测度收敛做了最基本研究：一致收敛是很强的收敛，在一般情况下很难实现，因而应用大受限制，而处处收敛和几乎处处收敛的条件相对弱一些。

下面，笔者研究了测度有限可测集上几乎处处有限的可测函数列和一般可测集上的几乎处处有限的单调可测函数列几乎处处收敛、近一致收敛和依测度收敛3种收敛之间的等价条件。

1 基本概念

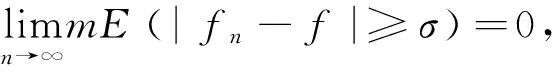
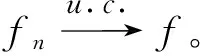
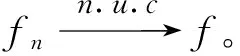
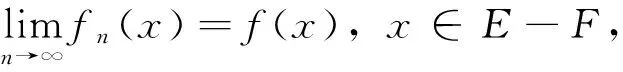
引理1[1]设f和{fn}n≥1都是E上几乎处处有限的可测函数，则：

i){fn}n≥1在E上几乎处处收敛于f,当且仅当对任意的ε>0，有：

ii){fn}n≥1在E上近一致收敛于f,当且仅当对任意的ε>0，有：

引理4[6]设f和{fn}n≥1都是E上几乎处处有限的可测函数，若{fn}n≥1在E上近一致收敛于f，则{fn}n≥1在E上依测度收敛于f。

引理5[7-9](勒贝格Lebesgue定理) 设f和{fn}n≥1都是E上几乎处处有限的可测函数，若mE<+∞且{fn}n≥1在E上几乎处处收敛于f，则{fn}n≥1在E上依测度收敛于f。

引理6[7-9](Riesz定理) 设f和{fn}n≥1都是可测集E上的几乎处处有限的可E测函数，若{fn}n≥1在E上依测度收敛于f，则{fn}n≥1存在子列{fnk}k≥1在E上几乎处处收敛于f。

2 主要结论

定理1设f和{fn}n≥1都是E上几乎处处有限的可测函数，且{fn}n≥1为E上的单调函数列，若{fn}n≥1在E上几乎处处收敛于f，则{fn}n≥1在E上依测度收敛于f。

证明由{fn}n≥1在E上几乎处处收敛于f，可得对任意的ε>0，有：

成立，记E0=E(fn(x)→f(x))，对于任意的x0∈E0，则{fn(x0)}n≥1单调收敛于f(x0)，于是有:

|fn+1(x0)-f(x0)|≤|fn(x0)-f(x0)|

成立。因此，对任意ε>0，E0(|fn+1-f|≥ε)⊂E0(|fn-f|≥ε)，即E(|fn-f|≥ε)，为单调递减集族，于是由测度的性质可得：

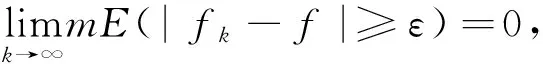
注：在mE<+∞条件下，几乎处处收敛,近一致收敛和依测度收敛彼此等价。

引理7设f和{fn}n≥1都是E上几乎处处有限的可测函数，且对于任意x∈E，满足以下条件之一：

i)f1(x)≤f2(x)≤f3(x)≤……≤fn(x)≤fn+1(x)≤……≤f(x)；

ii)f1(x)≥f2(x)≥f3(x)≥……≥fn(x)≥fn+1(x)≥……≥f(x)，

则E(|fn-f|≥ε)为单调递减集族。

证明事实上，对于任意x∈E，若f和{fn}n≥1满足以上条件之一，则对于任意n≥1有:

|fn+1(x)-f(x)|≤|fn(x)-f(x)|

于是，对于任意ε>0，由|fn+1(x)-f(x)|≥ε可得|fn(x)-f(x)|≥ε，所以:

E(|fn+1-f|≥ε)⊂E(|fn-f|≥ε) (n≥1)

成立，即E(|fn-f|≥ε)为单调递减集族。

定理2设f和{fn}n≥1满足引理7的条件，则在E上{fn}n≥1几乎处处收敛于f与{fn}n≥1依测度收敛于f彼此等价。

证明对于任意ε>0，由引理7可知E(|fn-f|≥ε)为单调递减集族，则有:

成立，于是由引理1可得几乎处处收敛与依测度收敛彼此等价。

定理3设f和{fn}n≥1满足引理7的条件，则在E上{fn}n≥1近一致收敛于f与{fn}n≥1依测度收敛于f彼此等价。

证明对于任意ε>0，由引理7可知E(|fn-f|≥ε)为单调递减集族，则有:

成立，于是由引理1可得近一致收敛与依测度收敛彼此等价。

3 结 语

主要利用几乎处处收敛和近一致收敛的等价刻画，进一步考察了各种收敛之间的强弱关系，通过对几种收敛关系定理的讨论和分析，可以看出在几种收敛关系中各种前提条件的重要性，几乎处处收敛、近一致收敛和依测度收敛彼此等价的条件除了可测集的有界性mE<+∞外，函数序列的单调性也可以保证以上3种收敛彼此等价。由此可见序列的单调性也是一个较为重要条件，因此外界条件的改变使得各种强弱不同的收敛得到了统一，进一步增强了对可测函数在理论上的理解和应用。

[1]温华永.叶果洛夫定理的一个新证明[J].四川师范大学学报，2000，23(6)：576-577.

[2]袁守成.可测函数序列的完全收敛性[J].株洲师范高等专科学校学报，2007，12(5)：28-29.

[3]张玲.几种收敛间的关系[J].高等数学研究，2005，8(4)：12-15.

[4]林谦.关于可测函数列的各种收敛性[J].云南师范大学学报，1994，14(1)： 8-17.

[5]杨洁.关于可测函数列各种收敛性的几点注记[J].工程数学，1998，14(2)： 120-123.

[6]尹敏.可测函数列的几种收敛性之间的关系[J].井冈山师范学院学报， 2001，22(6)：42-44.

[7]程其襄.张奠宙，魏国强，等.实变函数与泛函分析基础[M].第2版.北京：高等教育出版社，2003：205-206.

[8]夏道行.实变函数论与泛函分析 [M].第2版.北京：高等教育出版社,1985:185-190.

[9]严加安.测度论讲义[M].北京：科学出版社,2004.

[编辑] 洪云飞

10.3969/j.issn.1673-1409.2011.10.003

O175.1

A

1673-1409(2011)10-0010-02